连续配筋混凝土路面力学行为的温度效应

钟春玲，李 娜，孟广伟

（1.吉林建筑大学，长春130118；2.吉林大学机械科学与工程学院，长春130022；3.中元国际（长春）高新建筑设计院有限公司，长春130000）

0 引 言

连续配筋混凝土路面（CRCP）是在路面纵向配置连续的钢筋，中间不设横向胀缩缝，与普通混凝土路面相比，其耐久性和整体性以及行车舒适性都较好，而且CRCP的养护维修费用小，在欧洲和美国被广泛采用［1－2］。在CRCP的设计计算过程中，冬夏温差产生的路面变形受到地基及连续钢筋的约束，所以CRCP的温度应力是造成路面破坏的主要因素［3－4］，它往往超过荷载应力成为路面设计的主要控制指标。

国内外学者对CRCP的温度效应进行了研究，形成了设计规范，并给出了该类路面的设计指标［5－6］。设计规范存在一定的局限性，例如我国的设计规范不能考虑裂缝宽度等因素的影响，而AASHTO设计方法则是基于观测数据得出的经验公式。

对CRCP开裂情况的研究，国外学者主要采用现场观测和加速加载试验的方法［7－8］，缺乏深入的理论分析。同样我国学者也对CRCP的裂缝发展情况进行了现场观测［9］。在理论分析方面，国内学者典型的研究成果为以两条相邻裂缝之间的路段为研究对象，假定裂缝处钢筋的位移为零，推导了CRCP在季节性温差作用下受力性能［10－11］。然而在实际工程中，裂缝处钢筋的位移并不为零，使得各裂缝间隔段存在耦合，从而导致现有的理论求解模型在端部区域存在较大误差。

为了解决上述问题，基于有限元方法的基本理论，建立了连续配筋混凝土路面力学行为的温度效应分析模型。该理论模型最大的特点是能够考虑裂缝处钢筋的实际位移当作约束条件，从而考虑各裂缝间隔段的耦合效应。此特点决定了用本文的理论分析模型可以精确计算出温度作用下连续配筋混凝土路面整个路段各区段的静力响应。

1 理论模型的建立

1.1 基本假定

如图1所示，CRCP通常在端部设置锚固地梁来约束由于混凝土干缩和温度变化引起的路面位移（见图1（a））。也可以通过计算在端部设置桥梁用伸缩缝的方式满足端部位移（见图1（b））。因为在连续配筋混凝土路面中，钢筋是等间距布置的，根据弹性力学基本原理可取出任意含一根钢筋、宽度为一个钢筋间距的板条进行分析。基本假定如下：①钢筋和混凝土之间的粘结应力与两者之间的位移差成正比；②地基摩阻应力与混凝土路面板的位移成正比；③假设混凝土路面板与地基始终不脱离［5］。

图1 连续配筋混凝土路面Fig.1 Continuously reinforced concrete pavement

1.2 求解方程的形成

单元模型如图2所示，路面在温度应力作用下的位移包括混凝土路面板的轴向位移uc（x），钢筋的轴向位移us（x）。混凝土路面板与连续钢筋的粘结应力系数为ks，地基摩阻力系数为kc。

1.2.1 单元的位移模式

在连续配筋混凝土路面中，钢筋位于路面的中性层位置，先给出钢筋的位移模式对结构分析的影响，令钢筋的纵向位移为

如图3所示，根据微元体的受力平衡关系可得：

式中：As为钢筋的横断面面积；Ac为混凝土板的截面积；ds为钢筋直径；b为混凝土路面板的宽度；σs为钢筋应力；σc为混凝土应力；τs为钢筋与混凝土之间的粘结应力；τc为混凝土路面板与地基之间的摩阻应力。

图2 单元结点位移Fig.2 Node displacement of element

图3 微元体Fig.3 Micro-unit

由式（2）可知：

式中：εs为钢筋的应变；Es为钢筋的弹性模量；Ec为混凝土的弹性模量。

由材料力学可知：

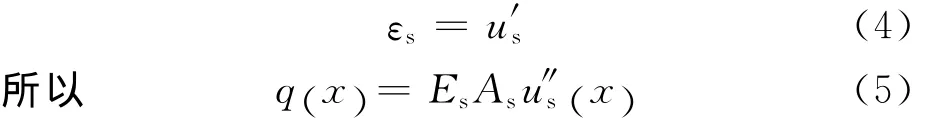
由基本假定可知：

根据式（1）（3）（5）（6）可得：

式中：c1＝（EsAs）／Ks，Ks＝ks·∑πds。

由式（1）（7）（8）可得：

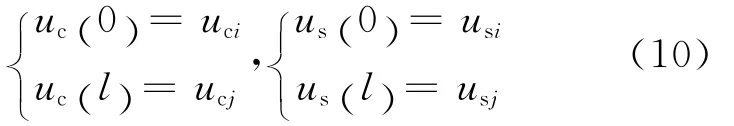
将式（10）代入式（1）和式（9）可得

写成矩阵形式为

1.2.2 单元的几何方程

令混凝土路面板和连续钢筋的应变分别为εc（x）、εs（x）。根据式（4）和弹性力学的基本原理可知，单元上任意点的应变可表示如下：

式中：B为应变矩阵：

根据式（7）（8）可知连续钢筋与混凝土路面板之间的滑移量为

1.2.3 单元的物理方程

2.1.2拯救濒危物种加快实施中华鲟、长江鲟、长江江豚等长江珍稀水生生物拯救行动计划，建立完善的自然种群监测、评估与预警体系。在三峡水库、长江故道、河口、近海等水域建设一批中华鲟接力保种基地。制定中华鲟规模化增殖放流规划。在长江中下游夹江、故道、水库、湖泊等水域建设一批长江江豚迁地保护水域。支持有条件的科研单位和水族馆建设长江珍稀濒危物种人工繁育和科普教育基地。

（1）应力与应变的关系

根据弹性力学的基本原理，路面单元的节点力列阵可表示为

（2）钢筋与混凝土之间的粘结力与滑移量之间的关系

（3）混凝土的位移与地基摩阻力之间的关系

假定在一个单元内地基摩阻力与混凝土路面的位移之间的关系为线性，则地基应力为

式中：

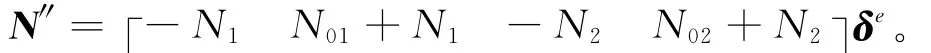
1.2.4 单元的刚度方程

设单元结点力列阵为

则单元的总势能为

式中：Kc＝kcb。

根据最小势能原理，对系统的势能函数π取一阶变分，并令π的一阶变分为零：

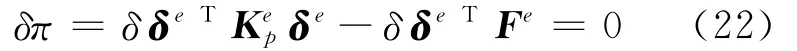
由式（22）可得到路面部分的单元刚度方程为

2 算例分析

利用上述公式，分析了降温30℃时（假设施工温度为10℃，统计资料表明长春地区月平均最低气温为－20℃），图4为一条1000 m长的CRCP的位移和应力状态，其中板厚为25 cm，钢筋间距为10 cm，ds＝14 mm，钢筋和混凝土的线膨胀系数α＝1.0×10－5，kc＝4 kPa／mm，Ec＝3.25×107k Pa，Es＝2.1×108k Pa，ks＝50×103kPa／mm。CRCP中钢筋和混凝土的位移计算结果如图5～图7所示。

图4 CRCP裂缝分布图Fig.4 Crack distribute of CRCP

图5给出的是全路段钢筋和混凝土路面板的位移状态，图6给出的是路段坐标0～8 m范围内的钢筋和混凝土路面板的位移状态，图7给出的是路段坐标496～504 m范围内的钢筋和混凝土路面板的位移状态。根据图4给出的裂缝分布情况，可知路段在坐标为2 m、4.25 m、6.25 m处均存在裂缝，从图6中可以看出，裂缝处的钢筋位移不等于零，图7中混凝土位移有突变的位置即为裂缝存在的位置。从图6和图7中可以，看出在降温作用下CRCP的钢筋位移不等于零，但是在路面的中段区域裂缝处的钢筋位移较小。因此当端部设置的桥梁用伸缩缝时，应采用全路段联合分析CRCP的位移和应力状态。

图5 路面位移曲线Fig.5 Displacement curve of pavement

图6 路面端部位移状态Fig.6 Displacement magnifier of pavement end

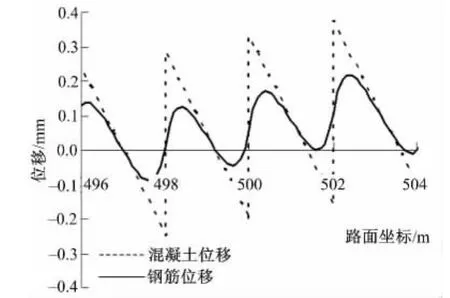
图7 路面中段位移状态Fig.7 Displacement magnifier of pavement mid

为了说明上述计算理论的合理性，利用本文推导的计算理论结合裂缝发展规律得到的裂缝平均间距和文献［9］中的观测结果进行了对比分析，如图8所示，可以看出二者吻合得较好，说明利用本文的分析方法能够较为精确地计算连续配筋混凝土路面在温度作用下的位移状态。

图8 裂缝间距随混凝土龄期的变化Fig.8 Crack spacing vs.age of concrete

图9 路面位移对比分析Fig.9 Comparative analysis of pavement displacement

目前对CRCP位移的计算大多采用文献［11］给出的计算理论，该理论是取一个裂缝间隔段单独分析，以裂缝处的钢筋位移为零作为前提进行计算，由于忽略了各个裂缝间隔段的相互作用，会给计算结果带来一定的误差，本文计算理论考虑了路面全长内所有裂缝间隔段的联合作用，更符合实际受力情况。二者的计算结果如图9所示，可以看出：以某路段端部计算出的钢筋和混凝土位移，均与以该路段中部计算出的相应位移存在一定差异，混凝土的位移最大相差20%左右，在道路的端部区域差别较大，说明本文给出的计算结果有较高的应用价值。

对于两端设置伸缩缝的CRCP，其端部位移的计算是控制伸缩缝设置类型的关键，因此本文给出了不同地基摩阻力系数对端部位移的影响，如图10所示。从图10可以看出，地基摩阻力系数越大，端部位移越小，说明地基对路面板的约束越强，从控制端部位移的角度分析，地基摩阻力系数越大对结构越有利。

图10 地基摩阻力系数与路面端部位移的关系Fig.10 Relatioship between subgrade friction and displacement of pavement end

3 结束语

基于有限元方法，建立了连续配筋混凝土路面力学行为的温度效应分析模型。该模型最大的特点是能够考虑裂缝处钢筋位移的实际状态，从而考虑各裂缝间隔段的耦合效应。采用数值模拟方法计算了温度作用下连续配筋混凝土路面整个路段各区段的静力响应，并与现有的计算理论进行了对比分析。结果表明本文给出的计算理论有较高的推广应用价值。最后给出了设置伸缩缝的连续配筋混凝土路面端部位移与地基摩阻力系数的对应关系，为设置伸缩缝的允许宽度提供了理论依据。

［1］查旭东，王燕，韩春华.欧洲水泥混凝土路面综述［J］.国外公路，1999，19（3）：16-22.

Zha Xu-dong，Wang Yan，Han Chun-hua.Summary of cement concrete pavement in Europe［J］.Journal of Foreign Highway，1999，19（3）：16-22.

［2］McCullough B F.Criteria for the design，construction and maintenance of continuously reinforced concrete pavement［J］.Australian Road Research， 1983，13（2）：79-99.

［3］陈云鹤，邓学钧，杨树才，等.连续配筋混凝土路面早期裂缝宽度分析［J］.中国公路学报，1998，11（Sup）：36-42.

Chen Yun-he，Deng Xue-jun，Yang Shu-cai，et al. Analysis of crack width in continuously reinforced concrete pavement（CRCP）at early ages［J］.China Journal of Highway and Transport，1998，11（Sup）：36-42.

［4］陈锋锋，黄晓明，秦永春.连续配筋混凝土路面横向裂缝分布模型的研究［J］.公路交通科技，2006，23（6）：18-21.

Chen Feng-feng，Huang Xiao-ming，Qin Yongchun.Study on the probability distribution model of continuously reinforce concrete pavement transverse cracks［J］.Journal of Highway and Transportation Research and Development，2006，23（6）：18-21.

［5］中华人民共和国交通部.公路水泥混凝土路面设计规范（JTG D40-2002）［S］.北京：人民交通出版社，2002.

［6］AASHTO.AASHTO Guide for Design of Pavement Structures［M］.Washington DC：AASHTO，1993.

［7］Kohler E，Roesler J.Crack spacing and crack width investigation from experimental CRCP sections［J］. International Journal of Pavement Engineering，2006，7（4）：331-340.

［8］Gharaibeh Nasir G，Darter Michael I，Heckel Laura B.Field performance of continuously reinforced concrete pavement in Illinois［C］∥Transportation Research Record，1999，1684：44-50.

［9］查旭东.连续配筋混凝土路面横向开裂发展规律［J］.交通运输工程学报，2008，8（2）：65-68.

Zha Xu-dong.Elastic solution for thermal stress in continuously reinforced concrete pavement（CROP）［J］.Chinese Journal of Applied Mechanics，2000，17（4）：36-42.

［10］曹东伟.连续配筋混凝土路面结构研究［D］.西安：长安大学，2001.

Cao Dong-wei.Research on structure of continuously reinforced concrete pavement［D］.Xi＇an：Chang＇an University，2001.

［11］曹东伟，胡长顺.连续配筋混凝土路面温度应力分析［J］.西安公路交通大学学报，2001，21（2）：1-5.

Cao Dong-wei，Hu Chang-shun.Analysis of the thermal stress for continuously reinforced concrete pavement（CRCP）［J］.Journal of Xi＇an Highway U-niversity，2001，21（2）：1-5.