教材分析与教学设计构想

梁佳维

摘 要：教学设计构想仅是一种教学活动计划框架，主要包括学习目标的确立、教材内容的优化、教材潜能的挖掘与学习过程的构建这四个方面，它在一定程度上对优化课堂教学起着决定性作用。教学设计构想包括“分析内容要点，确立学习目标；分析内容素材，优化学习资源；分析内容潜能，扩张学习功效；分析内容表述，构建学习过程”四个环节.

关键词：教材分析；教学设计构想；内容；学习

教学设计是依据课程标准并针对教材内容与学生的实际情况来制定具体教学活动计划的过程，而教学设计构想仅是一种教学活动计划框架，类似于论文写作提纲.教学设计活动构想，主要包括学习目标的确立、教材内容的优化、教材潜能的挖掘与学习过程的构建这四个方面，它在一定程度上对优化课堂教学起着决定性的作用.课标解读、教材分析与学情分析是教学设计构想活动的三个重要层面，本文就教材分析与教学设计构想这个层面，并以初中数学《二次函数与一元二次方程》课题为例，谈谈个人的认识.

一、分析内容要点，确立学习目标

教材是课程内容的载体，它是课标在内容和形式方面的具体体现，因此课程目标与教材内容密切相关.教学设计前对教材内容要点进行分析，它不仅是对课标的具体解读，而且也是制定课题学习目标的重要过程 [1 ].

教材内容要点，它主要指教材中所涉及的知识与方法要点，其中方法主要包括研究方法、数学思想以及分析方法.如北师大版中的《二次函数与一元二次方程》课题，它主要为三个要点：（1）以竖直上抛的实际问题提出“二次函数图像与一元二次方程根的关系”问题；（2）探讨二次函数图像和x轴的交点与一元二次方程的根的关系；（3）示例二次函数的图象求一元二次方程近似解过程与方法.其中的知识要点就是“二次函数图像和x轴的交点就是一元二次方程的根”，研究方法是“由具体到一般的归纳方法”，数学思想是“数形结合”思想，而解决问题的分析方法就是“图像方法”.

课题学习目标，它主要包括“知识与技能、过程与方法、情感态度与价值观”三维目标.对于前两维目标，一般从教材内容要点分析中就可以确定，而对于“情感态度与价值观”目标，它是“过程与方法”目标的衍生体，通常是针对“过程与方法”目标内涵来分析.

关于三维目标的表述，目前教师中存在两种表述形式，一种是分开表述，另一种是综合表述.本人倾向于综合表述，因为三维目标是一个有机的整体，它不能割裂.依据课程学习过程与效果关系，学习目标的表述通常为“过程与方法+知识与技能+情感态度与价值观”的表述模式，因此本课题的学习目标可表述为：（1）通过经历对二次函数图像特点的探究，认识图像在x轴上的交点与一元二次方程的根的关系，体验探究与发现的乐趣并领悟数形结合思想；（2）通过尝试练习，知道运用二次函数图像求一元二次方程近似解方法，认识图像方法的价值.不难看出，学习目标（1）中就隐含着教学重点，因此，确立了学习目标，也就确立了教学重点.

二、分析内容素材，优化学习资源

教材是依据课标来编写，对于知识与技能内容要点，课标有明确的规定，而对于说明或阐述其内容的案例素材，不同的编者有不同的选择.然而是否具有最佳的教学功能，它是教学设计构想过程必须考虑的问题，即在分析教材内容素材的基础上进行完善或变换的再度整合处理，目的是优化学习资源.

对于《二次函数与一元二次方程》的课题导入素材，本人以为应作如下两方面的处理.一是将课题导入中“竖直上抛运动”的问题背景改为 “喷水运动”.“竖直上抛运动”虽是学生非常熟悉的生活现象，但由于学生不知道“竖直上抛运动”的规律，因此无法理解教材中的位移公式h=-5t2+v0t+h0，对于那些喜欢刨根究底的学生，其思维自然会停留在对公式的质疑层面.如果学生提出“抛出的小球离抛出点的高度为什么是这样数学形式”，那么教师必定会处于尴尬的境地.不回答吧，自然会伤害学生的积极性，回答吧，确实不是几句话可以说清楚的问题.“竖直上抛运动”属于高中物理内容，对于其运动规律的探究，需要花费一节课的时间.可见，教材设计“竖直上抛运动”问题的案例素材，它给学生设置了一定的学习障碍.二是将问题情境改为有助于巩固二次函数知识与技能的问题情境，即要求学生根据图像写出其解析式.具体问题情境为：

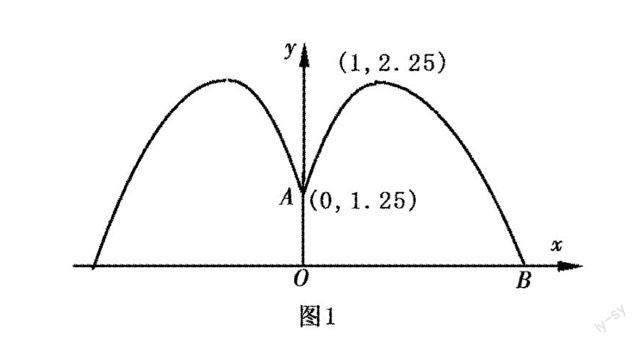
如图1所示，某校要在校园内建造一个圆形的喷水池，在水池中央安装一水管OA，O点在水面，OA=1.25m，A处喷出的水流做抛物线运动，抛物线的顶点离A点的水平距离为1m，离水面的高度为2.25m；（1）写出水流抛物线的解析式；（2）要使水流不落在池外，水池半径至少是多少？

对于喷水的抛物线运动，学生有直接的生活经验，不容怀疑.对于解析式，学生自然会从“顶点式”或“标准式”这两个角度来构建自己的思路，显然，它有助于学生对所学知识与方法的巩固.

教材处理是教材分析中的重头戏，也是教学设计的创新点.

三、分析内容潜能，扩张学习功效

所谓内容潜能，它主要指课题内容在促进学生对知识与技能的把握方面有着潜在的启发功能，通常是指教材内容中的隐性成分.因此，充分认识课题内容潜能是教学设计构想中有效地扩张学习功效的重要方面.课题的内容潜能主要包括课题地位作用与课题相关内容，下面分述之.

课题地位作用，它指课题中的知识与方法对单元学习或学段学习乃至跨学段学习的重要性.课题中的知识与方法，它可能是了解性的常识，也可能是单元中的核心内容，又可能是学习后续课程的基础，还可能是贯通不同模块的枢纽，课题地位作用是一种隐性因素，它要求教师站在整个课程内容结构的高度来审视课题.对于《二次函数与一元二次方程》课题，它不仅揭示了二次函数图像与一元二次方程的关系，而且蕴含着任意函数图像与相应方程的关系，它是图像法求方程近似解的通用方法.在后续的高中学习中，还要用到二次函数图像来分析一元二次不等式的解，另外还要借助“图像交点”涵义来研究几何图像的位置关系.应该说，本课题是贯通初高中数学课程知识与方法的枢纽，在初等数学中有着重要的地位与作用.

课题相关内容，它指与课题有着密切联系且有助于丰富或完善学生认知结构并有利于学生开展后续学习的那些知识与方法.由于课题目标的集中性与内容结构的重点性，教材难以将相关内容全部编入其中，加之“空白”策略有助于发展学生的贯通理解能力，因此教材也无须顾及所有角落.然而作为教师，他要明确与课题相关的内容.如 “二次函数与一元二次方程”关系，教材只研究了图像在x轴交点与方程根的关系，然而对于图像和x轴不相交条件与方程无解条件的关系，教材没有涉及.我们知道，这两个条件的分析，它可以为高中学习一元二次不等式解法奠定一定的能力与方法基础.再如运用图像求其它方程的近似解，也是课题的相关内容.

课题地位作用与相关内容分析实质是同一个思考范畴，所不同的是后者分析要求更具体以及考虑是否纳入课题且怎样纳入的策略问题.

四、分析内容表述，构建学习过程

内容表述，这里指教材内容的阐述方式.在《二次函数与一元二次方程》课题中，教材内容结构为“从生活实际现象来提出课题——引导学生探究二次函数图像与一元二次方程根的关系——示例图像法解一元二次方程方法”，“提出问题——探究问题——解决问题”是课题内容学习的主线，由“实践——认识——实践”是学生学习认知发展的过程特征.教材中“想一想”、“议一议”、“做一做”、“读一读”的编排体例，实质是教材对课题学习过程活动的建议.因此，认真分析教材中的内容表述方式是构建学习过程的主要途径.

应该说，教材为了有效贯彻新课程理念，所有的课题内容都显示了明确清晰的学习过程活动，而且便于课堂操作.如“议一议”中，教材是先引导学生对比观察y=x2+2x，y=x2-2x+1，y=x2-2x+2这三个函数图像在直角坐标系的分布特征，然后引导学生思考下列问题：（1）每个图像与x轴有几个交点？（2）一元二次方程x2+2x=0，x2-2x+1=0有几个根？解方程验证一下.一元二次方程x2-2x+2=0有根吗？（3）二次函数y=ax2+bx+c的图像和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系？一般说来，教师在教学中可以按教材操作，但基于“关注学生发展”的课程理念以及扩张课题内容的学习功效，通常要注意在教材内容的基础上进行适度的延伸或拓展.如上面的“议一议”过程，教师就可以增设以下问题来引导学生思考并讨论：①一元二次方程ax2+bx+c=0无根判别式是什么？二次函数y=ax2+bx+c的图像和x轴无交点的判别式是什么？②一次函数y=bx+c的图像与一元一次方程bx+c=0的根有何关系？其它函数图像与相应方程的根呢？显然，这种在教材对学习过程活动建议的基础上进行适度的扩张，它就是构想教学过程中“依据教材用活教材”的体现，其目的是丰富与完善学生的知识与方法结构.

教学设计构想仅是教学活动的计划框架，然而在具体的教学设计中，教师还须在分析学情的基础上来综合考虑教学方法的选择、教学手段的运用，突出重点的形式、难点突破的手段等诸多细节问题，然而它不是本文论述的范畴，敬请读者悉心体会.

参考文献：

[1]吴小玲.教师如何做好课堂教学设计[M].长春：吉林大学出版社，2004.