基于集合经验模态分解敏感固有模态函数选择算法的滚动轴承状态识别方法
王玉静 康守强 张 云 刘 学 姜义成 Mikulovich V I
基于集合经验模态分解敏感固有模态函数选择算法的滚动轴承状态识别方法
王玉静①②康守强②张 云①刘 学②姜义成*①Mikulovich V I③
①(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)②(哈尔滨理工大学电气与电子工程学院 哈尔滨 150080)③(白俄罗斯国立大学 明斯克 220030)
为了更有效地提取滚动轴承各状态振动信号的特征,该文提出了一种基于集合经验模态分解(EEMD)的敏感固有模态函数(IMF)选择算法。该算法对振动信号经EEMD分解后得到的固有模态函数采用峭度值、相关系数相结合的方法自动提取其敏感分量,以此获得振动信号的初始特征。再运用奇异值分解和自回归(AR)模型方法得到滚动轴承各状态振动信号的特征向量,并将其输入到改进的超球多类支持向量机中进行智能识别,从而实现滚动轴承的正常状态,不同故障类型及不同性能退化程度的各状态识别。实验结果表明,相比基于经验模态分解结合自回归模型或奇异值分解的特征提取方法,该方法可更有效地提取滚动轴承故障特征信息,且识别精度更高。
信号处理;状态识别;非平稳信号;集合经验模态分解(EEMD);敏感固有模态函数(IMF)
1 引言
滚动轴承是支撑旋转轴的关键部件,广泛应用于各种机械设备之中。现有的诊断方法大多集中在滚动轴承故障位置的诊断,而不同故障程度的识别是最近研究的新方向[1]。这也对提取滚动轴承振动信号的有效特征提出了新的挑战。
经验模态分解(Empirical Mode Decomposition, EMD)方法适合分析处理非平稳、非线性信号[2]。基于EMD的特征提取方法在各领域得到了广泛的应用,如文献[3]采用基于EMD的希尔伯特能量谱作为语音和非语音的鉴别特征,结合顺序统计滤波器提高了对语音信号的检测率;文献[4]提出一种基于EMD的弹道目标平动补偿与微多普勒特征提取方法,并通过仿真实验验证了其有效性和鲁棒性;文献[5]采用EMD方法来提取齿轮故障振动信号的特征;文献[6,7]采用EMD结合AR模型分别对滚动轴承故障类型、故障类型及不同性能退化程度振动信号进行特征提取,获得了较好效果。
EMD本身也存在一些不足,为了抑制EMD的模态混叠现象,文献[8]提出了一种集合经验模态分解(Ensemble EMD, EEMD)方法。文献[9]对被测信号序列进行等间隔二次采样,之后再运用EEMD的思想对信号进一步处理,应用到穿墙雷达人的运动微多普勒特性分析中,获得了较好效果。但EEMD分解结果取决于人为设定的总体平均次数与加入噪声的幅值大小这两个参数,还受筛选条件的限制,导致EEMD分解出的固有模态函数(IMF)仍可能存在模态混叠。再者,在EEMD分解过程中,分解出IMF的个数受原始信号点数的制约,这就可能造成EEMD的过分解[8]。从另一个角度,滚动轴承振动信号经EEMD,得到的IMF分量中,通常只有部分IMF包含大量故障信息,对故障敏感。因此,非常有必要研究一种方法来选择有效的,且对故障敏感的IMF,剔除噪声干扰成份或者与故障无关的伪分量,凸显故障特征。文献[10]提出了利用各IMF峭度最大来选取滚动轴承振动信号EEMD分解后的敏感IMF的方法。各IMF峭度值可能有多个大于3,对利用IMF进一步提取特征来说,取最大的峭度值对应的一个IMF会丢失部分故障信息。目前广泛应用的敏感IMF选择算法是相关系数法,计算各IMF与原信号的归一化相关系数,但该方法需要人为确定一个阈值来选择敏感IMF分量,文献[11, 12]中,设定阈值为最大相关系数的1/10。对于不同的信号,该阈值同样需要人为调整。
另一方面,在智能分类方法中,支持向量机(SVM)有其独特的优势并被广泛应用。文献[13]在基于EMD的提取特征基础上,采用SVM对常规低分辨雷达体制下空中飞机目标进行分类,获得了较好的识别效果。对于多分类问题,基于超球结构支持向量机[14]及改进的分类规则[15],文献[7]又进一步进行了完善,并应用到滚动轴承的多类故障分类中,获得了较好效果。
因此,本文在分析EEMD方法理论的基础上,提出了峭度值与相关系数相结合的自动提取滚动轴承振动信号敏感IMF算法,之后结合奇异值分解(SVD),自回归(AR)模型参数估计进一步提取特征,并引入改进的超球多类支持向量机来进行多状态识别,最终实现滚动轴承的正常状态、故障类型(内、外环)及不同性能退化程度的各状态识别。
2 振动信号特征提取
2.1 集合经验模态分解
EEMD方法的本质是一种叠加高斯白噪声的多次经验模式分解,利用了高斯白噪声具有频率均匀分布的统计特性,通过每次加入同等幅值的不同白噪声来改变信号的极值点特性,之后对多次EMD得到的相应IMF进行总体平均来抵消加入的白噪声,从而有效减少模式混淆问题[8]。EEMD分解步骤如下:
(1)初始化总体平均次数;


(4)对所得含噪声的信号x()分别进行EMD分解,得到如式(2)的各自IMF和的形式:

式中c,j()为第次加入白噪声后分解得到的第个IMF,r,j()是残余函数,代表信号的平均趋势,是IMF的数量;
(5)重复步骤(3)和步骤(4)进行次,每次分解加入幅值不同的白噪声信号得到IMF的集合为
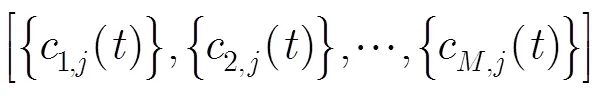
(6)利用不相关序列的统计平均值为零的原理,将上述对应的IMF进行集合平均运算,得到EEMD后的最终IMF,即


(7)EEMD分解的最终结果为

式中()为残余分量。
2.2 自动提取敏感IMF分量算法
峭度系数是一个常用的时域统计指标,正常状态下,高斯分布的峭度系数约为3,当峭度系数大于3时就预示着故障的出现,根据不同频带的峭度变化趋势可以更有效地选择对故障敏感频带[16]。
峭度指标定义:

峭度系数是无量纲的时域指标,它波动较大,不适合强噪声环境下的状态监测问题。对最初始退化时微弱故障反应不十分敏感,在故障后期(故障程度较大)退化过程中峭度值呈高-低-高的变化[17]。因此,单独根据峭度值不能有效衡量故障程度,也不能准确判断出故障的类型。



综上,为了不丢失故障信息,并且达到初步特征提取,获取敏感IMF的目的,本文采用自动相关系数法和IMF峭度系数法(峭度系数大于3)分别选取IMF,并以二者的并集作为敏感IMF。为进一步进行特征提取做准备。
2.3 构造特征向量矩阵及特征提取流程
为了进一步提取振动信号的特征,在上述提出敏感的IMF分量的基础上,进一步采用AR模型和奇异值分解的方法来构造特征向量。

由于AR模型参数、残差方差和奇异值在数值单位上差距较大,为了使后续分类不出现权值分配混乱现象,对所有特征值采用线性函数进行归一化处理。因此,构造每个振动信号归一化后的特征向量矩阵为

式中max为AR模型的最大阶数,小于max的模型参数补零,使所有参数个数一致;为敏感IMF的数量。
特征提取流程如图1所示。

图1 振动信号特征提取流程图
对于滚动轴承多状态分类,由于学习信号和测试信号不止一个,而多个信号分别经过EEMD分解提取敏感IMF分量的个数可能不同,设最大个数为,不足的用零向量进行补充。之后对每个振动信号的个IMF分别求AR模型参数、残差方差,同时将个IMF组成特征向量矩阵求取个奇异值,构造归一化特征向量矩阵为
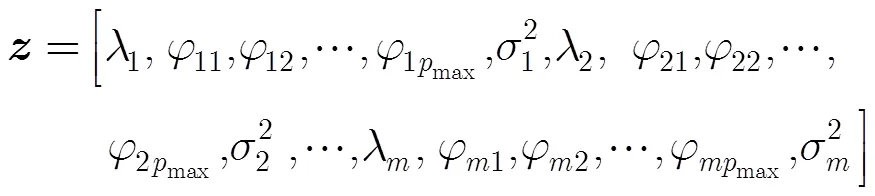
3 滚动轴承各状态识别
由于改进分类规则的超球结构多类支持向量机处理多分类问题时,在补充新类样本、各样本间数据不均衡、分类精度方面具有一定的优势[7]。因此,本文选用该分类器对滚动轴承多状态进行分类。根据文献[7]改进的分类规则重写如下:
测试特征向量不包含在关键区域,则

测试特征向量包含在关键区域,该区域中的训练样本集合为空时,则

测试特征向量包含在关键区域,该区域中的训练样本集合不为空时,则

式中所有参数的含义参见文献[7]。
4 滚动轴承各状态识别方法流程
基于集合经验模态分解,自动提取敏感IMF分量算法,奇异值分解和改进超球多类支持向量机的滚动轴承各状态识别方法的步骤如下:
(1)采集大量的滚动轴承振动信号,包括正常状态、不同故障类型及不同性能退化程度振动信号;
(2)按8倍交叉验证法将信号分为训练信号和测试信号;
(3)对各状态的每个训练信号进行特征提取,按照式(9)构造特征向量矩阵;
(4)各状态的所有学习信号构造特征向量矩阵:


(5)求得各状态超球的参数,确定初始状态超球;
(6)采用相同的方法求得测试信号的特征,按照式(9)构造特征向量矩阵;
(7)基于特征向量矩阵,根据式(10),式(11)和式(12)判断测试信号对应的滚动轴承的状态。当诊断正确率最高时,确定超球的参数;
(8)实际现场振动信号,同样提取出特征向量,根据式(10),式(11)和式(12)评判现场滚动轴承的健康状态。
5 应用与分析
基于美国西储大学轴承数据中心的型号为6205-2RS滚动轴承振动数据[18],本实验利用该滚动轴承正常工作情况下、内外环故障情况下的5种状态数据进行研究。其中滚动轴承内、外环不同故障程度的数据包括:内、外环损伤直径0.18mm的故障数据和内、外环损伤直径0.53mm的故障数据。5种状态滚动轴承数据,每个样本数据长度1024点,信号的采样频率为12 kHz。

表1给出了部分滚动轴承在正常状态和故障状态下,对振动信号进行EEMD分解得到的IMF的峭度值和振动信号与各IMF之间的相关系数。
由表1可以看出,滚动轴承故障状态振动信号敏感IMF的选取取决于峭度值法和相关系数法,为了获取全面的故障信息,取二者的并集。比如内环故障,大于3峭度值的IMF有IMF1, IMF2, IMF4,相关系数法选取小于阈值0.2973的敏感IMF有IMF1, IMF2, IMF3,事实上通过求取IMF3和IMF4的包络谱可以得到其包含有故障频率164 Hz的信息,因此取二者的并集作为敏感IMF。对于滚动轴承正常状态震动信号,敏感IMF的选择取决于相关系数法。另外,如果采用最大相关系数的1/10作为相关系数法的阈值(分别为0.05436, 0.08892, 0.09835),则选取故障振动信号的敏感IMF均多出2~3个IMF,多出的IMF包络谱上故障频率处的幅值约为零。

表1 IMF的峭度值及与振动信号的相关系数

图2 内环故障信号及其EEMD分解
从对表1中给出的滚动轴承3个振动信号的分析可以得出,取峭度值法和相关系数法的并集确定敏感IMF数量,正常的为前5个,内环故障为前4个,外环故障为前4个。通过对实验中大量滚动轴承振动信号进行敏感IMF提存,得知敏感IMF的最大个数=5,因此对于敏感IMF个数小于5的,用零向量进行补充。按照式(9)构造一个信号的特征向量矩阵,滚动轴承第状态的N个振动信号按照式(13)构造特征向量矩阵。将输入到改进的超球支持向量机中进行训练,获得的分类器的参数如表2所示。表2给出了基于其它特征提取方法的分类器参数。在该参数下获得的平均识别率和一个振动信号识别的平均时间如图3所示。
表2故障诊断方法比较

特征提取方法改进的超球支持向量机参数 Cs EMD+Yule-Walker0.232.10.965 EMD+Ulrych-Clayton0.132.10.940 EMD+SVD0.585.10.975 EEMD+敏感IMF+(SVD结合Ulrych-Clayton)0.142.10.955
从图3可以看出,本文方法比其它方法在识别一个振动信号状态时所消耗的平均时间多。原因为敏感IMF的提取算法计算量小,并且该算法选出来的敏感IMF由原来经验选取的6个降到5个,使后续的特征提取和分类耗时减小。但由于EEMD多次加入高斯白噪声进行多次分解,其耗时比EMD耗时多,AR模型的Ulrych-Clayton[7]参数估计较Yule- Walker[7]或SVD耗时多;上述原因综合使得总的识别时间增加。但同时换取了更高的平均识别率,比已有的基于EMD结合Ulrych-Clayton的特征提取方法平均识别率高出2%,可见本文所提出的特征提取方法更有效。
6 结论
本文提出了一种基于集合经验模态分解的峭度值结合相关系数的敏感固有模态函数选择算法,相关系数法的阈值采用所有相关系数的标准差。为了获取更有效更全面的故障特征,敏感IMF由峭度值法和相关系数法的敏感IMF的并集构成。该方法减小了人为选取敏感IMF的主观性。基于此,提出EEMD敏感IMF, SVD, AR模型结合改进的超球多类支持向量机方法实现滚动轴承的正常状态、不同故障位置及性能退化程度的各状态识别。
滚动轴承振动实验结果表明,敏感IMF选择算法可以全面有效地提取包含故障信息的IMF。基于敏感IMF的EEMD, SVD, AR模型的Ulrych- Clayton参数估计的特征提取方法,再利用改进的超球多类支持向量机来识别滚动轴承各状态的方法是有效的。与基于EMD结合AR模型参数或SVD的方法相比所耗时间虽然长,但换取了较高的平均识别率。
[1] Pan Yu-na, Chen Jin, and Li Xing-lin. Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means[J]., 2010, 24(2): 559-566.
[2] Huang N E, Shen Z, Long S R,.. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time A series analysis[J]., 1998, 454(1971): 903-995.
[3] 卢志茂, 金辉, 张春祥, 等. 基于HHT和OSF的复杂环境语音端点检测[J]. 电子与信息学报, 2012, 34(1): 213-217.
Lu Zhi-mao, Jin Hui, Zhang Chun-xiang,.. Voice activity detection in complex environment based on Hilbert-Huang transform and order statistics filter[J].&, 2012, 34(1): 213-217.
[4] 罗迎, 柏又青, 张群, 等. 弹道目标平动补偿与微多普勒特征提取方法[J]. 电子与信息学报, 2012, 34(3): 602-608.
Luo Ying, Bai You-qing, Zhang Qun,.. Translational motion compensation and micro-doppler feature extraction of ballistic targets[J].&, 2012, 34(3): 602-608.
[5] 程军圣, 于德介, 杨宇, 等. 基于EMD的齿轮故障识别研究[J]. 电子与信息学报, 2004, 26(5): 825-829.
Cheng Jun-sheng, Yu De-jie, Yang Yu,.. Research on gear fault diagnosis based on EMD[J].&, 2004, 26(5): 825-829.
[6] Cheng Ju-sheng, Yu De-jie, and Yang Yu. A fault diagnosis approach for roller bearings based on EMD method and AR model[J]., 2006, 20(2): 350-362.
[7] 康守强, 王玉静, 杨广学, 等. 基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法[J]. 中国电机工程学报, 2011, 31(14): 96-102.
Kang Shou-qiang, Wang Yu-jing, Yang Guang-xue,.. Rolling bearing fault diagnosis method using empirical mode decomposition and hypersphere multiclass support vector machine[J]., 2011, 31(14): 96-102.
[8] Wu Zhao-hua and Huang Norden E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]., 2009, 1(1): 1-41.
[9] 王宏, Narayanan R M, 周正欧, 等. 基于改进EEMD的穿墙雷达动目标微多普勒特性分析[J]. 电子与信息学报, 2010, 32(6): 1355-1360.
Wang Hong, Narayanan R M, Zhou Zheng-ou,.. Micro- doppler character analysis of moving objects using through- wall radar based on improved EEMD[J].&, 2010, 32(6): 1355-1360.
[10] 胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]. 中国电机工程学报, 2012, 32(11): 106-111.
Hu Ai-jun, Ma Wan-li, and Tang Gui-ji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J].,2012, 32(11): 106-111.
[11] 林丽, 余轮. 基于相关系数的EMD改进算法[J]. 计算机与数字工程, 2008, 36(12): 28-29,38.
Lin Li and Yu Lun. Improvement on empirical mode decomposition based on correlation coefficient[J].&, 2008, 36(12): 28-29,38.
[12] Peng Z K, Tse P W, and Chu F L. A comparison study of improved Hilbert-Huang transform and wavelet transform: application to fault diagnosis for rolling bearing[J]., 2005, 19(5): 974-988.
[13] 王宝帅, 杜兰, 刘宏伟, 等. 基于经验模态分解的空中飞机目标分类[J]. 电子与信息学报, 2012, 34(9): 2116-2121.
Wang Bao-shuai, Du Lan, Liu Hong-wei,.. Aircraft classification based on empirical mode decomposition[J].&, 2012, 34(9): 2116-2121.
[14] 朱美琳, 刘向东, 陈世福. 用球结构的支持向量机解决多分类问题[J]. 南京大学学报 (自然科学版), 2003, 39(2): 153-158.
Zhu Mei-lin, Liu Xiang-dong, and Chen Shi-fu. Salving the problem of Multi-class pattern recognition with sphere- structured support vector machines[J].(), 2003, 39(2): 153-158.
[15] 故磊, 吴慧中, 肖亮. 基于新的决策规则的球形支持向量机分类算法[J]. 系统仿真学报, 2008, 20(11): 2901-2904.
Gu Lei, Wu Hui-zhong, and Xiao Liang. Sphere-structured support vector machines classification algorithm based on new decision rule[J]., 2008, 20(11): 2901-2904.
[16] 杨国安. 机械设备故障诊断实用技术[M]. 北京: 中国石化出版社, 2007: 244-245.
[17] 潘玉娜, 陈进. 小波包-支持向量数据描述在轴承性能退化评估中的应用研究[J]. 振动与冲击, 2009, 28(4): 164-167.
Pan Yu-na and Chen Jin. Wavelet package-support vector data description applied in bearing performance degradation assessment[J]., 2009, 28(4): 164-167.
[18] Loparo K A. Bearing data center [EB/OL]. http://www. eecs.case.edu/laboratory/bearing/welcome_overview.htm, 2013.
[19] 陈略, 訾艳阳, 何正嘉, 等. 总体平均经验模式分解与1.5维谱方法的研究[J]. 西安交通大学学报, 2009, 43(5): 94-98.
Chen Lue, Zi Yan-yang, He Zheng-jia,.. Research and application of ensemble empirical mode decomposition principle and 1.5 dimension spectrum method[J]., 2009, 43(5): 94-98.
王玉静: 女,1983年生,博士生,研究方向为信号与信息处理.
康守强: 男,1980年生,副教授,研究方向为信号与信息处理.
姜义成: 男,1964年生,教授,研究方向为信号与信息处理.
Condition Recognition Method of Rolling Bearing Based on Ensemble Empirical Mode Decomposition Sensitive Intrinsic Mode Function Selection Algorithm
Wang Yu-jing①②Kang Shou-qiang②Zhang Yun①Liu Xue②Jiang Yi-cheng①Mikulovich V I③
①(,,150001,)②(,,150080,)③(,220030,)
In order to extract effectively the characteristics of each condition vibration signal for rolling bearing, a sensitive Intrinsic Mode Function (IMF) selection algorithm which based on Ensemble Empirical Mode Decomposition (EEMD) is proposed. First, for obtaining the initial characteristics of the vibration signal, the vibration signal is decomposed by using EEMD, and the sensitive components of obtained IMFs are extracted automatically by using kurtosis combined with correlation coefficient. Then, the feature vectors of each condition vibration signal of rolling bearing are obtained by using Singular Value Decomposition (SVD) and AutoRegressive (AR) model. The obtained feature vectors are regarded as the input of the improved hyper-sphere multi-class Support Vector Machine (SVM) for intelligent recognition. Thereby, the condition recognition of normal state, different fault types and different degrees of performance degradation of rolling bearing can be achieved. The experimental results show that, the proposed method can effectively extract fault characteristics information of rolling bearing more than EMD combined with AR model and EMD combined with SVD method, and the recognition rate is higher.
Signal processing; Condition recognition; Nonstationary signal; Ensemble Empirical Mode Decomposition (EEMD); Sensitive Intrinsic Mode Function (IMF)
TN911.7; TP18
A
1009-5896(2014)03-0595-06
10.3724/SP.J.1146.2013.00434
2013-04-02收到,2013-10-31改回
国家自然科学基金(51305109),高等学校博士学科点专项科研基金(20122303120010),留学人员科技活动项目择优资助和哈尔滨市科技创新人才专项基金(留学回国人员)(2013RFLXJ019)资助课题
姜义成 jiangyc@hit.edu.cn

