直升机中电磁耦合薄弱路径的确定方法

贾云峰吴 亮*李 红魏嘉利胡 修马 超

①(北京航空航天大学电子信息工程学院 北京 100191)②(陆航学院基础部 北京 101116)

1 引言

随着计算机技术、信息技术及智能技术在直升机上的应用，在直升机系统的有限空间内，设备的发射功率越来越大，接收机的灵敏度也越来越高，因此系统更容易受到电磁干扰[1]。为了保障系统的电磁兼容性，只要切断电磁兼容三要素中的任意一个就可以有效地抑制电磁干扰，改善系统的电磁兼容性。

在电磁耦合方面，随着电磁干扰现象的研究[2,3]，准确、快速的电磁数值计算方法得到了广泛的运用。机载电子系统由于系统内部物理尺寸相差巨大且结构复杂，导致剖分网格过多，计算时间和计算资源不可接受，而电磁拓扑为这一问题的解决提供了方法。电磁拓扑的思想[4,5]是将具有较大体积和复杂结构的系统分层剥离并转化为一些小体积、结构简单的分系统。其中电磁拓扑理论最经典的方法是BLT方程[6]，它通过建立各层之间的传递函数来实现复杂系统电磁耦合问题的研究。电磁拓扑理论得到了广泛的关注，文献[7,8]使用电磁拓扑对复杂传输线网络的耦合问题进行了研究分析，文献[4,9]应用电磁拓扑研究了电磁脉冲传播与耦合问题，文献[10]研究了多层电磁屏蔽条件下电子器件之间的相互耦合问题，文献[11]将矩形孔缝的耦合转换成传输线网络，并使用电磁拓扑计算了机箱的屏蔽效能。但随着电子设备集成度的增加，设备之间的耦合变得更加复杂，传统的电磁拓扑方法难以对系统进行准确的分层，且各独立单元之间传递函数的计算也异常复杂。

为了解决上述问题，本文首先利用电磁耦合的网络特性，将系统中设备的端口映射成顶点并形成耦合有向图，然后使用比较成熟的数值算法或试验获取孔缝耦合、线缆耦合、天线-线缆耦合等端口之间的S参数或者衰减特性，最后使用最短路径算法寻找系统的电磁薄弱环节，从而解决了复杂系统的电磁干扰耦合问题。

2 电磁薄弱路径分析

2.1 电磁薄弱路径确定流程

为了准确获取直升机电子系统中干扰源与敏感点之间的主要耦合路径，本文提出了一种电磁干扰耦合薄弱路径的确定方法，提取薄弱路径的流程如图1所示。该方法首先将电磁干扰耦合网络转换成有向图，然后使用电磁仿真工具和试验数据相结合的方法量化并化简有向图，最后采用Dijkstra算法寻找出有向图中的最短路径。根据有向图与耦合网络之间的对应关系，最终寻找出薄弱路径上的关键整改点，从而高效地解决电磁干扰耦合问题。

2.2 构建耦合有向图

本文首先将系统内的电磁干扰耦合方式分为：天线-天线，天线-线缆，机壳-机壳，线-线，共阻抗 5类[12]，并结合系统的工作原理图和电路原理图，找出系统可能的电磁干扰耦合路径。然后将耦合路径上的设备端口一一映射为顶点，再根据系统的耦合关系和能量传输方向将各顶点连接起来，并信号的传播方向，从而实现了电磁干扰耦合有向图标明的构建。

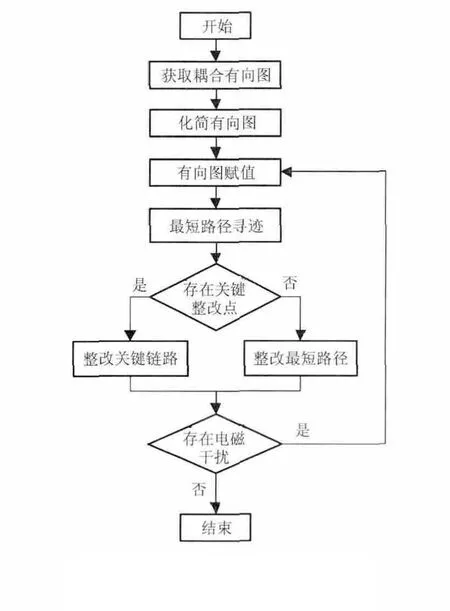
图1 电磁干扰耦合薄弱路径确定流程

典型电子系统的耦合示意图如图 2(a)所示，图中干扰源通过天线、线缆、孔缝等对敏感设备产生了干扰。将图 2(a)中的各端口等效成节点，形成的电磁耦合有向图如图2(b)所示(图2中没有标出电缆节点，因为该模型中不包括电缆耦合)。电磁波在实际传输过程中是进行双向传递，在这里仅考虑由干扰源向敏感体的单向传播。通常机箱孔缝数量比较多，在进行初始分析时可以对机箱的孔缝进行统一考虑，当确定孔缝是引起干扰的主要路径时，可以对孔缝进行进一步地细分，如图2(b)箭头所示，通过对有向图的深入分析，最终找出电磁干扰耦合通道的薄弱路径。

2.3 化简耦合有向图

对于单干扰对间的耦合有向图，即单个起始点和单个终止点，可根据图论知识计算出有向图中各个顶点的度，并标出有向图的分支，根据顶点的度和分支来简化有向图。化简的内容主要包括：删除电磁干扰耦合有向图中顶点的度为0的顶点，即去除系统中不干扰任何其它设备，也不会被其它设备所干扰的设备，如图3(a)所示，即删除节点4A，其中1A为干扰源，3A为敏感点；删除电磁干扰耦合有向图中与源点和终点不连通的子图，即去除系统中干扰能量不通过的设备，如图3(b)所示，即删除节点4B,7B,8B形成的子图，其中1B为干扰源，3B为敏感点；删除电磁干扰耦合有向图中不在源点和终点连通路径上的顶点，即去除系统中其它不相关的干扰源或敏感点，如图 3(c)所示，即删除图中的节点4C和节点7C，其中1C为干扰源，3C为敏感点。

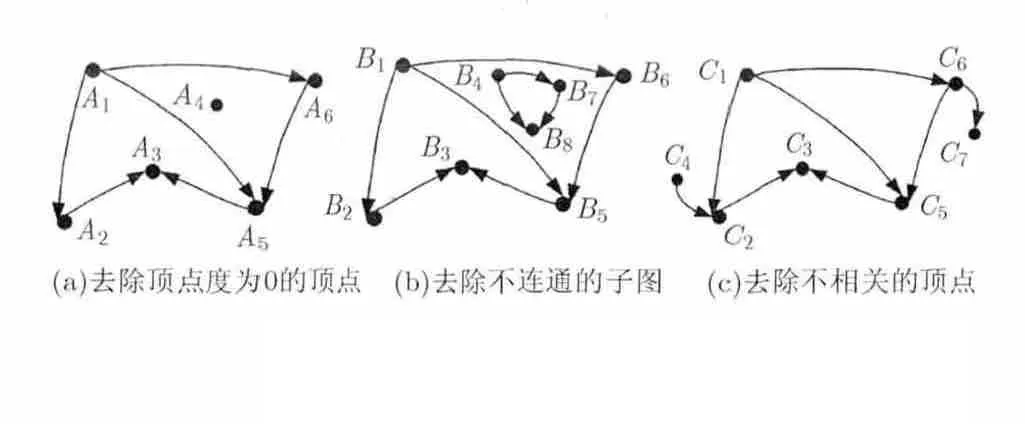
图3 电磁干扰耦合有向图化简

2.4 耦合有向图赋值

在单个干扰对间的电磁干扰耦合网络中，某个频点处的干扰能量在传递的过程中可能包含的损耗有：滤波器损耗fL，线缆损耗lL，线缆间耦合lA，天线-线缆耦合tlA ，天线-孔缝耦合taA ，天线间耦合等，将各损耗量用dB进行表示，则该链路上的总损耗量为

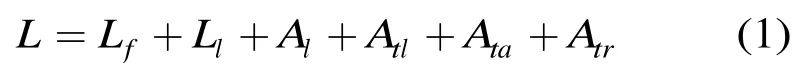
当某耦合路径是电磁干扰耦合网络中所有干扰能量损耗最小的路径时，即耦合有向图中的最短路径，因此可以用有向图的最短路径来表征电磁干扰耦合薄弱通道。其中，有向图中任意两顶点间的衰减量，可以通过仿真或试验的手段获得。在系统中，设端口i到端口j在频率f条件下的损耗值为ijL，则对应的有向图中顶点i到顶点j的一条边的数值就为ijL，且方向为i→j。为了准确地获取耦合有向图中所有的ijL，即耦合网络矩阵，对于干扰信号在滤波器和线缆中的损耗量，可以通过对滤波器和线缆两端的传递特性进行测试或计算来获取；天线-线缆间耦合的仿真和测试，采取逐一在某个天线或线缆端加入激励信号，而其它天线或线缆端接入负载，然后计算或测试天线-线缆间的损耗值；对于天线间的耦合，通过建立天线模型并进行仿真或测试，来得到各天线端口间的隔离度数据；线缆间耦合的获取，需要将带天线的线缆进行等效(例如带天线的线缆需要使用等效阻抗替换天线)，从而得到线缆间的损耗值。对于多线缆的耦合，同样需依次在某一线缆端加入激励信号，而其它线缆端接入等效负载，从而计算或测量该线缆和其它线缆间干扰信号的传递损耗值；对孔缝间耦合的粗分析，只计算机箱的整体屏蔽效能，在进行细分析时，需要对部分孔缝进行封闭来分别考虑不同孔缝的屏蔽效能。

2.5 薄弱耦合路径寻迹

图论与不断发展完善的计算机数据结构及算法的有效结合使得最短路径算法不断涌现，目前此类最短路径的算法大约有17种以上。文献[13]对其中的15种方法进行了测试，结果显示Dijkstra算法更适合于计算两点间的最短路径问题，但效率不高。文献[14]针对该算法的 3个缺点提出了一种改进的Dijkstra算法，Dijikatra算法在各个领域进行了广泛的应用[15,16]。耦合有向图中两顶点之间的最短路径可以说是最常见的最短路径问题，Dijkstra算法简单易用，是目前应用较多的算法，且采用结点-弧结构的存储结构，适合于本文中耦合有向图的求解，因此采用Dijkstra算法来进行最短路径寻迹。

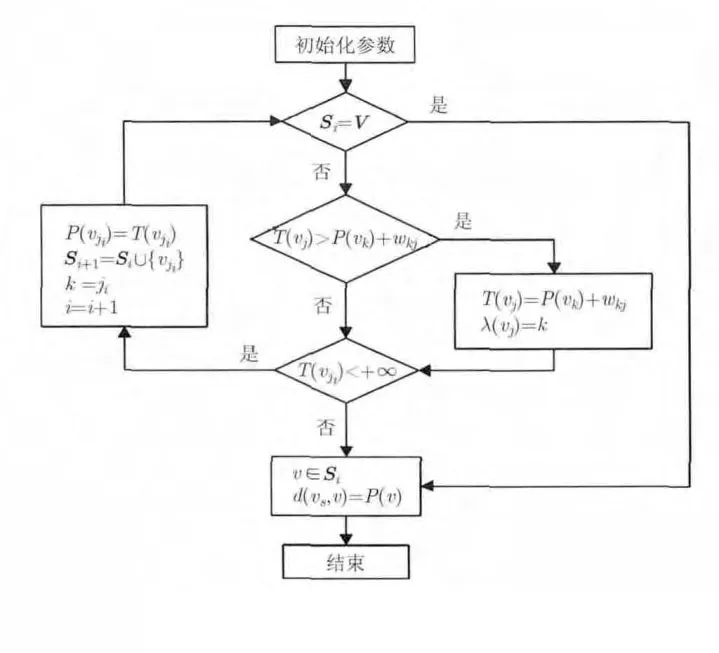
图4 最短路径寻迹流程图

(2)如果i=S V，寻找完毕，算法终止，这时对每个；否则转入(3)进行迭代计算。

2.6 链路关键点选取

单干扰对间耦合有向图的化简、赋值、寻迹方法同样适用于同频多设备对和多频多设备对。它们的不同点在于：在同频单设备对的有向图中只有单个源和敏感点，只需进行一次最短路径寻迹；同频多设备对的有向图中，拥有多个干扰源和多个敏感点，进行有向图化简时需要考虑所有干扰对，需要依次使用最短路径算法确定有向图中每一个干扰源和敏感点间的最短路径；多频多设备的有向图中，需根据每个分析频点得到多个单频多设备对的电磁干扰耦合有向图，并依次使用最短寻迹算法确定每一个有向图中的每一个干扰源到敏感体间的最短路径。

以上3种情况的电磁干扰耦合薄弱路径的关键点选取方法为：(1)同频单干扰对：只需针对最短薄弱路径上的设备进行整改，整改的关键点根据设备整改的效费比来确定。(2)同频多干扰对：(a)对于每一个敏感点，关键点为最短路径上所有干扰源到该敏感点的重叠路径；(b)对于每一个干扰源，关键点为最短路径上该干扰源到所有敏感点的重叠路径；(c)对没有重叠路径的最短路径，需考虑该最短路径上的每一个节点。(3)多频多干扰对：(a)将所有最短耦合路径上除了干扰源和敏感体的顶点按照顶点出现的次数进行排序；(b)出现次数最多的顶点为关键点，并去除关键点所在的薄弱路径；(c)判断出现次数次之的顶点是否在剩余的最短路径中，若在则为关键点，并去除关键点所在的薄弱路径，若不在则考虑下一个顶点，直至包含所有最短路径。

为了解决复杂系统的电磁干扰耦合问题，对关键点采取电磁兼容措施后，可再次判断系统是否仍受扰，若受扰则再次寻找最短路径，直到满足要求。线为线缆，Port指向部分表示天线。由该系统的组成框架和工作原理分析得出主要包含的干扰耦合网络如图6所示，并在此基础上使用FEKO建立相应的电磁兼容仿真模型。根据 2.4节的方法，机载天线-线缆间的耦合特性曲线和线缆间的耦合特性如图7所示。

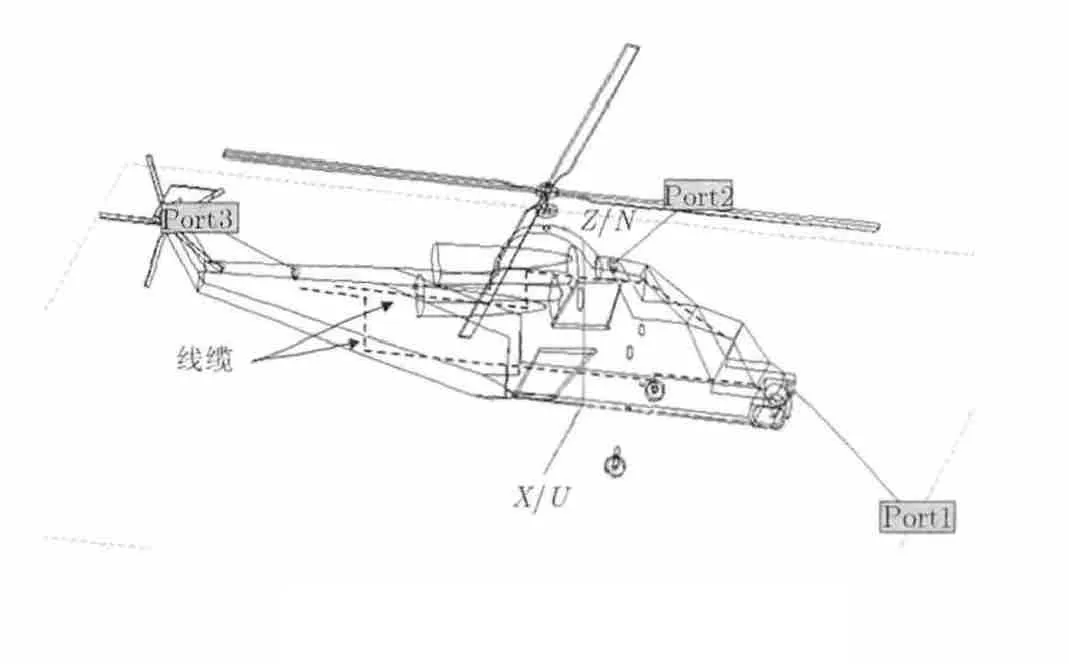
图5 直升机设备布局图

3 分析实例

采用本方法对某直升机上由电台和处理机组成的系统进行电磁干扰耦合薄弱路径的确定，直升机的外形、电缆分布和天线布局如图5所示，其中虚

由于该电台在200 MHz处受到处理机的干扰，因此计算每个设备在200 MHz处的电磁损耗量。按照该方法形成的电磁干扰耦合有向图如图8所示。其中主要包含了6条耦合路径，使用Dijkstra算法对图8中由顶点D2到顶点D13之间的有向图进行最短路径寻迹。表1表示了Dijkstra算法寻迹的结果，求得处理机到电台的最短路径长度为33，即从干扰源(处理机)到敏感设备(电台)的电磁损耗量为33 dB，也就是说该链路是该系统中传递电磁干扰信号能量最多的通道，即系统的电磁干扰耦合薄弱通道。其最短耦合路径为：处理机→处理机电源线A→电源滤波器→电台电源线B→电台。

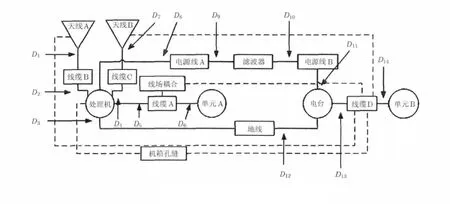
图6 电磁干扰耦合网络

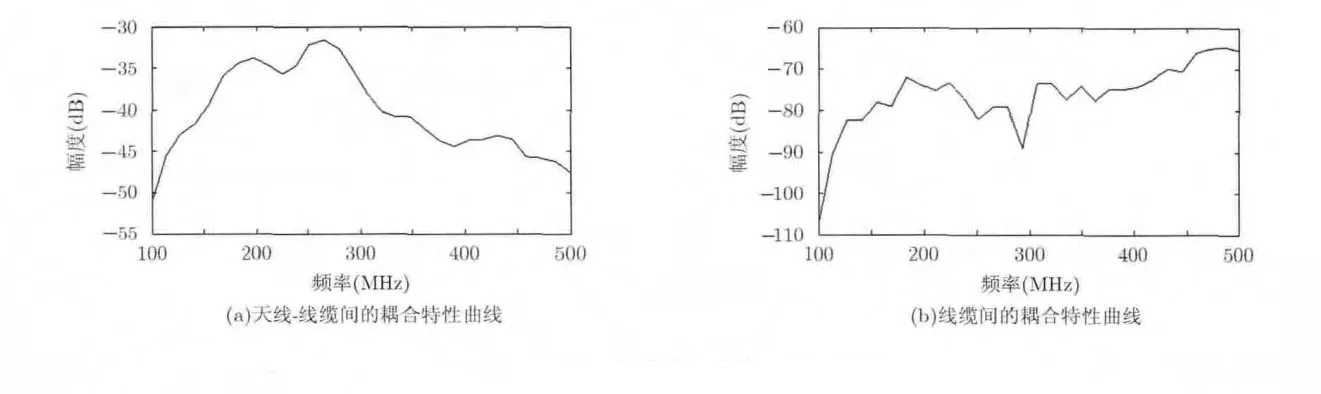
图7 耦合特性曲线

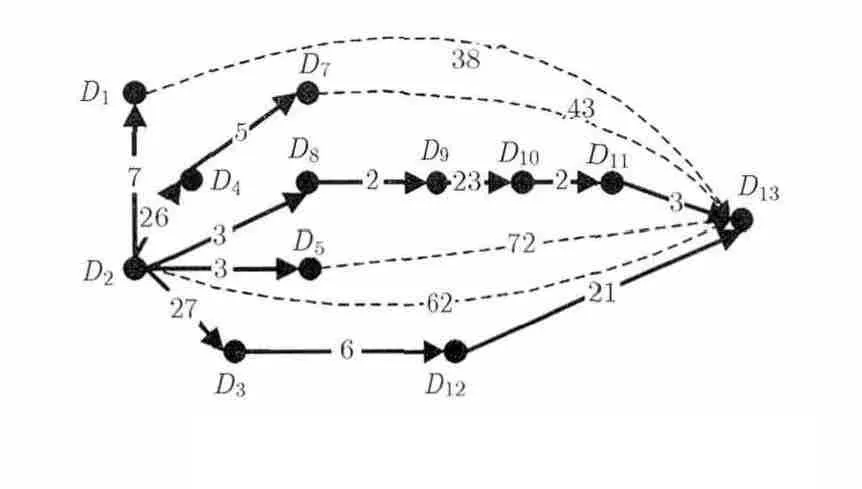
图8 电磁干扰耦合有向图

表1 电磁耦合路径

本例属于单干扰源和单敏感设备之间的干扰，只需对最短路径上的链路进行处理。本例中干扰信号是通过电源系统进行传播的，可以在处理机和电台的电源系统中加强滤波器在200 MHz附近的滤波效果，从而达到对干扰信号的抑制。根据寻迹结果还可以看出，干扰严重次之的路径是路径 1，如果路径3的抑制不够还可以对路径1采取相应的措施。路径3中包含有天线等强耦合器件，因此，在对路径3进行整改时，尽量不要改动天线的结构、位置等参数，因为初始的天线布局已经满足了天线隔离度的要求，再次变动会改变天线的布局设计等，此时可以在天线链路中加入滤波器增强带外抑制，或增加线缆的屏蔽效能。本文的主要耦合路径为路径3，在路径3处理机的电源线上加入滤波器，其滤波器对200 MHz干扰信号的抑制为14 dB，路径3的衰减量最终变为 47 dB。整改后干扰消失，从而实现对系统电磁兼容性的改善。

4 结论

本文针对机载电子系统的电磁干扰耦合问题，结合电磁兼容理论和图论的知识，对单频单干扰对电磁耦合有向图的创建、化简以及最短路径寻迹进行了详细的分析，并讨论了单频多干扰对和多频多干扰对电磁薄弱路径的确定方法。通过对单频单干扰对系统的电磁薄弱路径的分析，表明了该方法的可行性。通过该方法对电子系统薄弱环节的定位，为系统电磁兼容的预测和整改提供了有效的技术手段。

[1] 王星, 郝重阳, 陈游. 机载雷达与对抗设备电磁兼容建模与仿真[J]. 火力指挥与控制, 2010, 35(8): 1355-1358.Wang Xing, Hao Chong-yang, and Chen You. Modeling and simulation of EMC between airborne radar and counterdevice[J]. Fire Control and Command Control, 2010, 35(8):1355-1358.

[2] 朱文立. 国内外电磁兼容发展动态[J]. 电子质量, 2003, 7(1):62-64.Zhu Wen-li. The development of domestic and foreign EMC[J]. Electronics Quality, 2003, 7(1): 62-64.

[3] 苏东林, 王冰切, 金德琨, 等. 电子战特种飞机电磁兼容预设计技术[J]. 北京航空航天大学学报, 2006, 32(10): 1241-1245.Su Dong-lin, Wang Bing-qie, Jin De-kun, et al.. EMC predesign technologies on EW special aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006,32(10): 1241-1245.

[4] Tesche F M. Topological concepts for internal EMP interaction[J]. IEEE Transactions on Antennas and Propagation, 1978, 26(1): 60-64.

[5] Im Chang-hwan, Jung Hyun-kyo, and Kim Yong-joo. Hybrid genetic algorithm for electromagnetic topology optimization[J]. IEEE Transactions on Magnetics, 2003, 39(5): 2163-2169.

[6] Kang Won-june, Lee Vea-o, Mun Sang-kon, et al.. A study for the influence of the EM waves on the cavity with multirectangular apertures using BLT equation[C]. Preceedings of the IEEE Antennas and Propagation Society International Symposium (APSURSI), Toronto, ON, 2010: 1-4.

[7] Besnier P. Electromagnetic topology: an additional interaction sequence diagram for transmission line network analysis[J]. IEEE Transactions on Electromagnetic Compatibility, 2006, 48(4): 685-692.

[8] Wang Wei, Qin Yu-jian, and Liu Pei-guo. On the analysis of the load response of transmission line network based on electromagnetic topology-COG[C]. 10th International Symposium on Antennas, Propagation ＆amp; EM Theory(ISAPE), Xi’an, Oct. 22-26, 2012: 1069-1072.

[9] 李高升, 覃宇建, 刘培国, 等. 电磁拓扑结合积分方程求解电磁脉冲传播问题[J]. 现代电子技术, 2010, 23(1): 10-13.Li Gao-sheng, Qin Yu-jian, Liu Pei-guo, et al.. Method to solve electromagnetic pulse propagation based on combination of EMT and TDIE[J]. Modern Electronics Technique, 2010, 23(1): 10-13.

[10] 戴丽, 谢政, 罗建书, 等. 多层电磁屏蔽的电磁拓扑图分析方法[J]. 强激光与粒子束, 2006, 18(9): 1524-1526.Dai Li, Xie Zheng, Luo Jian-shu, et al.. Analytical method of multi-level shielding electromagnetic topological diagram[J].High Power Laser and Particle Beams, 2006, 18(9):1524-1526.

[11] Zhang Xu-feng, Li Ying, and Luo Jian-shu. Transmission line network model for evaluating the shielding effectiveness of a rectangular enclosure with apertures[C]. IEEE 4th International Symposium on Microwave, Antenna,Propagation, and EMC Technologies for Wireless Communications (MAPE), Beijing, 2011: 781-784.

[12] 陈琼, 蒋全兴, 周开基, 等. 电磁兼容性工程设计手册[M]. 北京: 国防工业出版社, 1993: 54-57.Chen Qiong, Jiang Quan-xing, Zhou Kai-ji, et al..Electromagnetic Compatibility Engineering Design Manual[M]. Beijing: National Defence Industry Press, 1993: 54-57.

[13] Zhan F B. Three fastest shortest path algorithms on real road networks[J]. Journal of Geographic Information and Decision Analysis, 1997, 1(1): 69-82.

[14] Wang Shu-xi and Zhao Xing-qiu. The improved Dijkstra,s shortest path algorithm[C]. Seventh International Conference on Natural Computation (ICNC), Shanghai, 2011:2313-2316.

[15] Wang Hui-juan, Yu Yuan, and Yuan Quan-bo. Application of Dijkstra algorithm in robot path-planning[C]. Second International Conference on Mechanic Automation and Control Engineering (MACE), Hohhot, 2011: 1067-1069.

[16] Cuan Ying and Chen Xiao-ni. Application of improved Dijkstra algorithm in selection of gas source node in gas network[C]. International Conference on Industrial Control and Electronics Engineering (ICICEE), Xi’an, 2012:1558-1560.