NURBS插补中相邻敏感点区域速度轨迹规划研究

董伯麟，何文杰

（合肥工业大学机械工程学院，安徽 合肥 230009）

1 引言

NURBS曲线作为一种参数曲线，可以表示大部分自由曲线，同时对该曲线也能实现高速高精度插补。目前为得到插补点的曲线参量，一般使用泰勒展开近似方法[1-2]。然而，这种方法简化时省略了高阶项，会产生截断误差，加剧插补速度的波动。文献[3]采用对分法计算插补点曲线参量。

文献[4]基于泰勒展开方法，提出了一种自适应速度插补方法，使插补速度根据弦误差和插补点曲率自适应地变化。文献[5]在自适应速度插补方法基础上，利用S型速度轨迹来限制加速度和加加速度，同时满足机床最大速度要求。文献[6]提出了一种具有相对完整的速度轨迹规划的NURBS插补算法，采用S形加速度轨迹曲线来实现加速度和加加速度的限定要求。文献[7]提出了采用S型加减速双向同步进行的插补算法，该算法简单高效。

另一方面，一些文献考虑相邻敏感点之间速度轨迹规划的交叉情况。文献[8]早期考虑了进给速度的波纹效应，然后提出了进给速度轨迹规划交叉的分类方法以及速度轨迹的拟合方法，但不够具体。文献[9]也提出了相邻敏感点速度轨迹规划交叉的解决方法，也没有具体分类。

因此，目的是处理相邻敏感点之间的速度规划。首先，由G1和G2不连续的断点和大曲率的关键点将NURBS曲线分段。采用S型加速度轨迹曲线得到更为平滑的速度轨迹，以减缓在曲线段连接处的速度波动。此外，提出了相邻敏感点之间的速度轨迹规划交叉的全部分类及对应的判定条件，同时针对每种类型进行速度轨迹规划。另外，考虑当前和下一插补敏感点区域的速度轨迹规划可能的情况，提出了整条曲线的速度轨迹规划方法。

2 NURBS插补

2.1 NURBS曲线定义

一条p阶的NURBS曲线C（u）定义如下[10]：

式中：｛Pi｝—控制点序列；｛wi｝—权因子；Ni，p（u）—第 i个 p 次 B样条基函数，它定义在非均匀节点矢量U=｛0，…，0，up+1，…，um-p-1，1，…,1｝上，其表达式定义如下：

由给定的曲线参量u，通过上式即可求出对应点。在求解NURBS曲线导矢时可采用文献[10]的方法。

2.2 NURBS曲线插补

计算插补点曲线参量一般使用泰勒展开近似方法。假设ti时刻对应的曲线参量为ui，则ti+1时刻的参量ui+1为：

式中：Ts—插补周期。

经推导，曲线参量u的二阶泰勒公式展开如下：

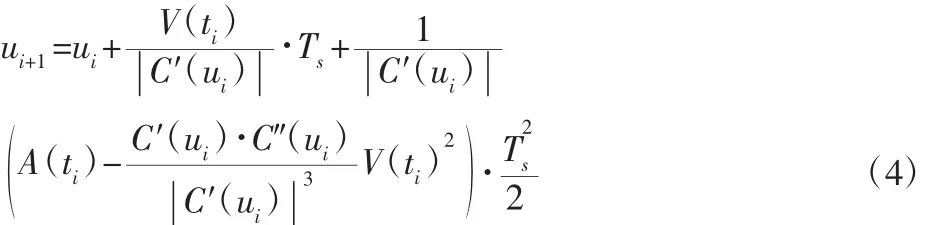
式中：A（ti）—ti时刻加速度；C′（ui）—NURBS曲线一阶导数；C″（ui）—NURBS曲线二阶导数。

2.3 弦误差受限的自适应速度

通过采取圆弧近似的方法，进给速度根据弦误差和曲线曲率自适应的变化[4]：

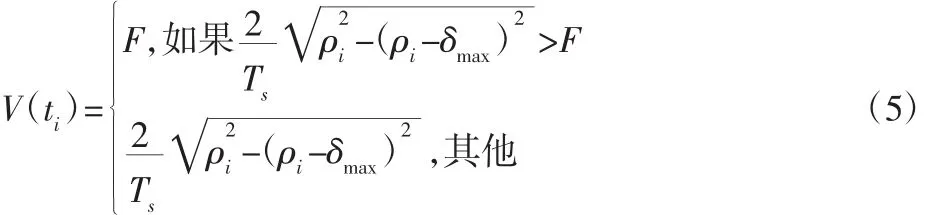
式中：V（ti）—自适应进给速度；ρi—曲线曲率；δmax—最大允许弦误差，ρi计算公式如下：

3 前瞻模块

3.1 敏感点搜索

在工件加工到速度敏感点时，进给速度会产生剧烈波动，使得加工质量产生恶化。速度敏感点包括断点（G0连续，G1不连续点和G1连续，G2不连续点）和大曲率的关键点。第一类断点和部分第二类断点位于节点处，可以在节点矢量中寻找[10]，非节点处的第二类断点可以通过粗插补的方法寻找曲线曲率突变的点。判据如下：

式中：ρi—第i个插补点的曲率半径。

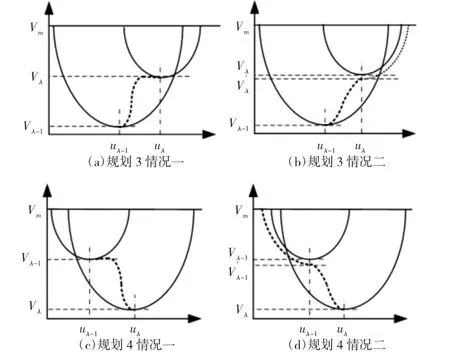
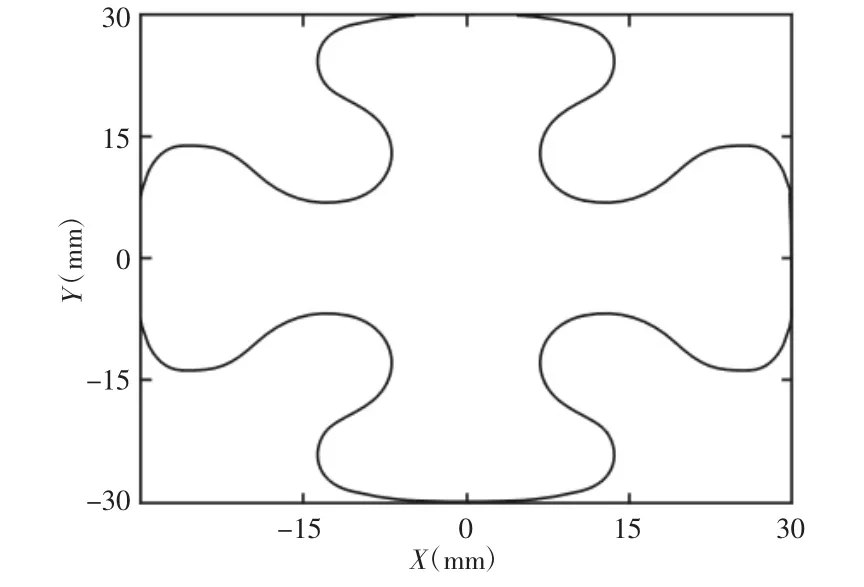
寻找关键点重点是确定曲线关键曲率。首先搜索曲率极大值的点作为备选关键点，再从从备选点中筛选出满足条件Vkr

Vkr=min）是根据弦误差和向心加速度的限制得到的修改的进给速度。

3.2 NURBS曲线段弧长计算

根据前瞻得到的信息，两个相邻敏感点之间曲线段的弧长就能够被近似计算：

式中：S（l）—整个曲线第l段的弧长；NBλ—该段第λ个敏感点所对应的插补点的下标。

4 速度轨迹规划和加减速

4.1 速度轨迹曲线

S型加速度轨迹曲线[9]使得加速度平滑变化，而加加速度也呈梯形变化，同时满足限定要求，得到的速度轨迹也更加平滑。所以利用文献[9]中提到的S型加速度轨迹曲线进行速度规划，如图1所示。

图1 S型加速度轨迹曲线Fig.1 S-Shaped Acceleration Profile

4.2 速度轨迹规划交叉

4.2.1 速度轨迹规划交叉类型

当NURBS曲线两相邻敏感点之间的弧长较小时，进给速度就不能加速至最大速度。即两敏感点的速度轨迹规划出现交叉。具体分为以下七类。

图2 速度轨迹规划交叉类型Fig.2 Intersection Types of Feedrate Scheduling

4.2.2 相邻敏感点区域速度轨迹规划

针对这些类型在进行速度轨迹规划时可分为以下五类：

规划1：速度轨迹规划不交叉，如图2（a）所示。

进给速度加速至速度限定值Vm，匀速行进至减速点后减速。

规划2：起始敏感点的加速和终止敏感点的减速阶段交叉，如图 2（b）、图 2（i）所示。

这两种类型速度轨迹规划类似，进给速度加速到某一速度值后减速。在寻找该中间速度时使用文献[8]中的二分法。

规划3：起始敏感点的加速和终止敏感点的加速阶段交叉，如图 2（d）所示。

（1）计算以起始敏感点的自适应速度开始，按照S型加速度轨迹曲线规律加速，刀具行进至终止敏感点时对应速度。

（2）若该速度大于终止敏感点的自适应速度，则可以加速至该速度后保持匀速至终止敏感点，如图3（a）所示。若小于终止敏感点自适应速度，则将原终止敏感点自适应速度调整为该速度（该速度小于原自适应速度，故弦误差满足要求），采用S型加速度轨迹曲线加速，如图3（b）所示。

规划4：起始敏感点的减速和终止敏感点的减速阶段交叉，如图 2（g）所示。

该类型与类型 3 类似，两种情况分别，如图 3（c）、图 3（d）所示。

规划5：一敏感点速度轨迹规划包含另一敏感点速度轨迹规划，如图 2（e）、图 2（f）所示。

把被包含的敏感点从敏感点序列中剔除。

图3 相邻敏感点区域速度轨迹规划Fig.3 Feedrate Scheduling of Adjacent Sensitive Points Region

4.2.3 整条NURBS曲线的速度轨迹规划

上节只是考虑相邻敏感点区域速度轨迹规划，插补时当前插补敏感点区域和下一插补敏感点区域的速度轨迹规划会相互作用。在当前插补敏感点区域，首先判断速度轨迹规划交叉类型，并选择对应速度轨迹规划方法，与此同时判断下一插补敏感点区域速度轨迹规划交叉类型及对应方法。如果下一插补敏感点区域交叉类型为2-3，且需要调整起始敏感点的自适应速度，则需要对当前插补敏感点区域重新进行交叉类型判别。若交叉类型为3-2，则起始敏感点被剔除，需要重新对新的当前插补敏感点区域和下一插补敏感点区域进行交叉类型判别。

当前插补敏感点区域速度轨迹规划交叉只会出现类型1，2-1或2-4，2-2，2-3，3-1这几种情况。而类型3-1只可能出现在曲线第一个相邻敏感点区域。其他相邻敏感点区域不可能出现3-1，3-2的情况，因为每次当前插补敏感点区域交叉类型判别时，都会进行下一插补敏感点区域交叉类型判别，若出现3-1或3-2的情况，其起始或终止敏感点都会被剔除，所以不可能出现这两种类型。

当下一插补敏感点区域为该插补曲线最后一个曲线段时，此时终止敏感点的自适应速度为0，交叉类型只可能是1，2-3，2-4，3-2。对于类型 1，2-3，2-4，仍采用其原速度轨迹规划方法，而类型3-2，则按照类型2-3的方法进行速度轨迹规划，若出现起始敏感点的自适应速度调整，则还要对当前插补敏感点区域重新进行交叉类型判别。

5 算法实例验证

5.1 叶型曲线

下面以一条3次叶型NURBS曲线为例，如图4所示。通过仿真验证提出的基于相邻敏感点区域速度轨迹规划插补算法，检验其在速度平滑和运动学、动力学性能上的优越表现。

该曲线的控制点、权因子、节点矢量信息如下：

图4 叶型曲线Fig.4 Leaf-Shaped NURBS Curve

其弦误差和运动学限定要求，如表1所示。

表1 弦误差和运动学限定要求Tab.1 Chord Error and Parameters of Kinematic Constraints

5.2 算法分析

通过前瞻模块可知，该曲线存在着很多曲率极大值点且距离较近，可能会出现相邻敏感点区域速度轨迹规划交叉。后面利用该曲线对这里算法和自适应速度算法进行了比较。

在分别比较了自适应速度算法和提出算法的弦误差和速度轨迹之后，如图5（a）、图5（b）所示。可看出采用这里算法后速度轨迹更加平滑，满足了弦误差和进给速度的限定要求。在分别比较了两种算法的加速度和加加速度之后，如图5（c）、图5（d）所示。可看出采用这里算法后加速度轨迹也更平滑，同时保证了加速度限定要求。加加速度是梯形曲线变化，也保证了加加速度的限定要求。

图5 这里算法与自适应速度算法各参数对比Fig.5 Parameters Comparison Between Adaptive Algorithm and the Proposed Algorithm

6 结论

针对NURBS插补中弦误差、速度、加速度及加加速度的限定要求，以及可能出现的速度、加速度及加加速度突变的问题，从速度规划的角度考虑，对相邻敏感点区域速度轨迹规划进行了深入研究，以实现速度轨迹和加速度轨迹更加平滑，加加速度无突变，同时保证弦误差、速度、加速度、加加速度的限定要求。仿真结果表明，该算法得到的速度轨迹曲线平滑，加速度轨迹曲线呈S型变化，加加速度轨迹曲线呈梯形变化，同时都在限定范围之内，满足了机床加工的运动学和动力学要求。