多值广义混合似变分不等式和非扩张映射的迭代算法
殷 羽
(重庆工商大学派斯学院,重庆合川 401520)
变分不等式问题是应用数学中一个重要的研究领域,它不仅在非线性最优化中具有广泛应用,而且在微分方程、力学、控制论、对策论、经济平衡理论、社会和经济模型等许多方面都有着重要的应用[1-5].最近,文献[1]利用Wiener-Hopf方程技巧给出了一个寻求非扩张映射S不动点集合与经典变分不等式问题解集合公共元素的迭代算法,此处在文献[1]的基础上研究一类更一般的多值广义混合似变分不等式,并将文献[1]中算法的迭代参数条件放宽,提出了不同于文献[1]的迭代算法,并在较弱的条件下证明了由算法所生成的迭代序列强收敛于非扩张映射不动点集合与多值广义混合似变分不等式解集合的公共元素.
设H是一个实Hilbert空间,其内积和范数分别为<·,·>和‖·‖,K是一个H中的非空闭凸集,CB(H)为H中所有的非空有界闭子集族.设T,A:H→CB(H)为集值映象,N:H×H→H是单值映射,φ(·,·):H×H→R∪{+∞}是一个关于两个分量都连续的二元泛函,S:H→H是非扩张映射.现在考虑多值广义混合似变分不等式问题:求u∈H,x∈Tu,y∈Au,s.t

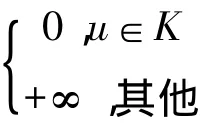
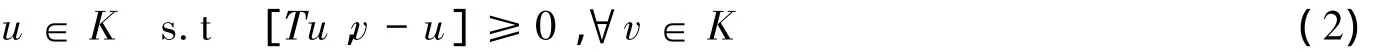
定义1 设T,A:H→CB(H)为集值映射,称映射N:H×H→H
(i)在第一变元关于T为β-强单调的,如果存在常数β>0,使得

(ii)在第一变元关于T为μ-Lipschitzian连续的,如果存在常数μ>0,使得

类似,可定义N·,·[]在第二变元关于A的强单调和Lipschitzian连续性.
定义2 设T:H→CB(H)为集值映射,称T在H上是M-连续的,如果{un}⊂H和un→u*,则在CB(H)的Hausdorff度量M下有T(un)→T(u*).
引理1[2]假设{a'n}{b'n}和{c'n}是3个非负实数序列,且满足条件
引理2[3]给定u∈H,z∈H,满足变分不等式
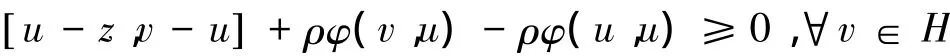
当且仅当u=Jφz(其中 ρ≥0 是常数,Jφ=(I+ρ∂(·,u))-1≡(I+ρ∂φ(u))-1).
众所周知,预解算子Jφ是非扩张映射.显然由引理2可知u∈H,x∈Tu,y∈Au是问题(1)的解当且仅当u∈H满足

注1 设S:H→H是非扩张映射,F(S)和GMVI(N,φ)分别表示映射S的不动点集和广义混合似变分不等式⑴的解集合.如果u∈F(S)∩GMVI(N,φ),那么u∈F(S)且u∈GMVI(N,φ),从而由式(3)可知,当且仅当u∈H满足

其中ρ≥0是常数,令z=u-ρN(x,y),则不动点式(4)可以改写成
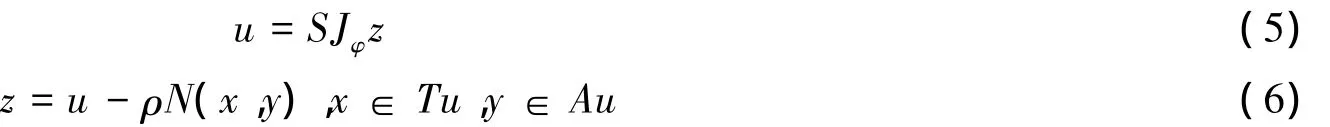
根据不动点式(5)(6),此处给出一个新的寻求非扩张映射S不动点集合与广义混合似变分不等式问题(1)解集合公共元素的迭代算法.
算法1 对于给定z0∈H,变分不等式问题(1)的近似解序列{un}{xn}{yn}由迭代方式(7)-(10)确定:
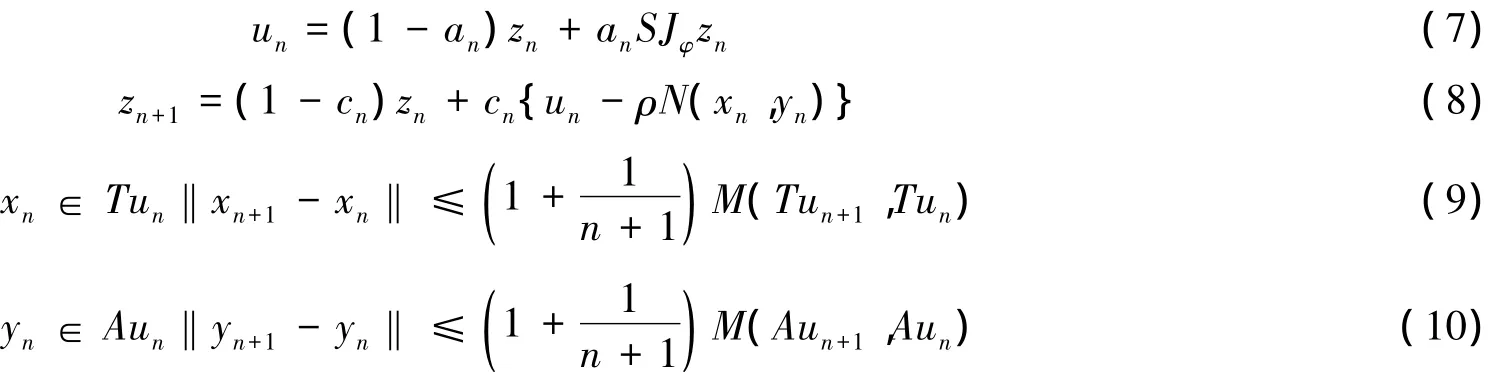
其中,an,cn∈[0,1](n=0,1,2,…),S:H→H是非扩张映射.

算法2 对于给定z0∈H,变分不等式问题(2)的近似解序列{un}由以下迭代方式确定:
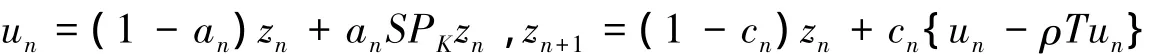
其中,an,cn∈[0,1](n=0,1,2,…),S:H→H是非扩张映射.
注2 算法2把文献[1]算法3.1中的迭代参数an放宽成可以是不同的迭代参数an,cn.类似,还可以得到各种已知或者新的作为算法1特例的算法,下面讨论算法1的收敛性.


证明 设z*∈H∈Tu*∈Au*是不动点式(5)(6)的解,相应的u*=SJφz*∈F(S)∩GMVI(N,φ),则由式(5)(6),有

由式(8)(13),有

由N在第一变元关于T为β-强单调和在第一变元关于T为μ1-Lipschitzian连续的定义有
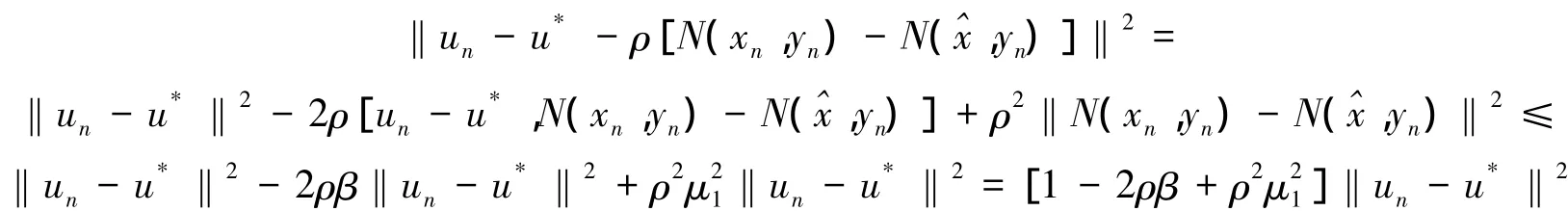
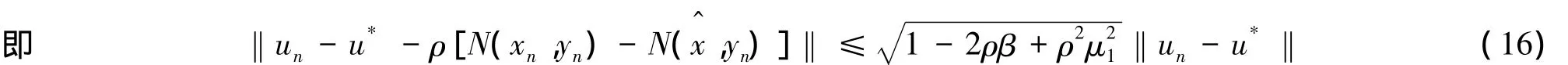
由N在第二变元关于A为μ2-Lipschitzian连续的定义有
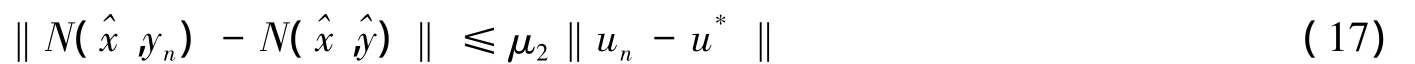
由式(14)-(17)有
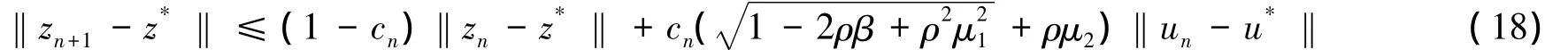
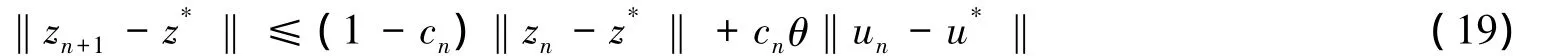
由式(7)(12)及算子S和预解算子Jφ的非扩张性又有
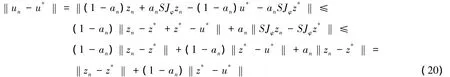
将式(20)代入式(19)得
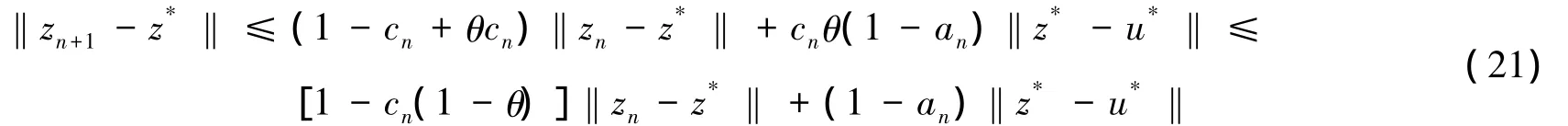

[1]NOOR M A,HUANG Z Y.Wiener-Hopf Equation Technique for Variational Inequalities and Nonexpansive Mappings[J].Applied Mathematics and Computation,2007,191(2):504-510
[2]CHANG S S,JOSEPH L H W,CHAN C K.Generalized System for Relaxed Cocoercive Variational Inequalities in Hilbert Spaces[J].Appl Math Lett,2007,20:329-334
[3]NOOR M A.Iterative Methods for General Mixed Quasivariational Inequalities[J].Journal of Optimization Theory and Applications,2003,119(1):123-136
[4]NOOR M A.Mixed Quasi Variational Inequalities[J].Applied Mathematics and Computation,2003,146:553-578
[5]万波.广义集值混合似变分不等式的迭代算法[J].西南师范大学学报:自然科学版,2008,33(3):1-4
[6]万波,江哓涛,曹于忠.一般混合似变分不等式的隐式迭代算法[J].纯粹数学与应用数学,2009,25(2):384-389
[7]罗光耀,王文惠,万波.用扰动逼近算法解一般混合似变分不等式组[J].西南大学学报:自然科学版,2009,31(4):39-43
[8]AUBIN J P,CELLINA A.Differential Inclusions[M].New York:Springer-Verlag,1984
[9]BORDER K C.Fixed Point Theorems With Applications to Economics and Game Theory[M].Cambridge:Cambridge University Press,1985

