关于四元数矩阵的一些不等式
宋 雪,冉 慧
(重庆大学数学与统计学院,重庆 401331)
近年来,对四元数体上代数问题的研究越来越深入,而四元数本身在众多的应用问题中也存在广泛的联系(如四元数在量子力学、刚体力学方面的应用),四元数在计算机图形图像处理、识别和空间定位方面的应用,引起了国内外许多学者对四元数体的研究与关注.此处将一些数学中经典的初等不等式推广到了四元数矩阵上.
1 定义和引理
定义1 设A∈Hn×n,如果A*=A,则称A是H上的一个n阶自共轭矩阵,其全体记为H(n,*).
定义2 设A∈Hn×n,如果A*A=AA*=In,则称A是H上的一个n阶酉矩阵,其全体记为H(n,u).


定义5 设A∈Hn×n,如果A*A=AA*,则称A是正规矩阵.
定义6 设A1,A2,…,Am(m≥2)为可交换的n阶四元数正规矩阵,它们的平方平均、算术平均、几何平均和调和平均分别定义为

引理1[1]设A∈H(n,*),则A酉相似于实对角矩阵,即存在U∈H(n,u),使得U*AU=diag(λ1,λ2,…,λn),其中 λ1,λ2,…,λn∈R 为A的n个特征值.
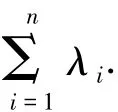

引理4[3]设A∈H(n,*),则存在实数a>0,使得A+aIn正定.
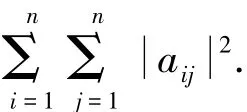
2 主要结果
2.1 Wielandt-Hoffman定理在四元数矩阵上的推广

证明 (i)若A>0,由于A∈H(n,*),C∈H(n,*),B=C-A,可知B∈H(n,*).则由引理 1,存在酉矩阵U1,U2,U3,使得

由于A>0,则 αi>0(i=1,2,…,n).显然有




(ii)若A不正定,则由引理4,存在实数a>0,使得A+aIn正定.由证明(i)可得
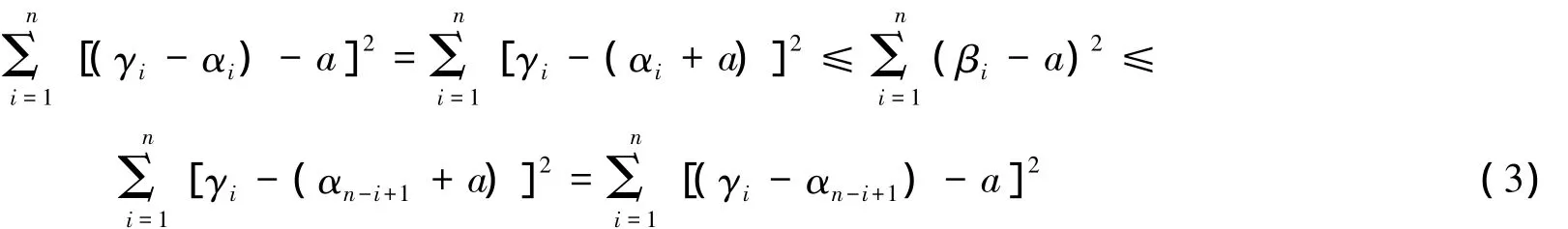
推论1 在定理1的条件下,设B=(Bij)∈H(n,*),则式(4)成立.
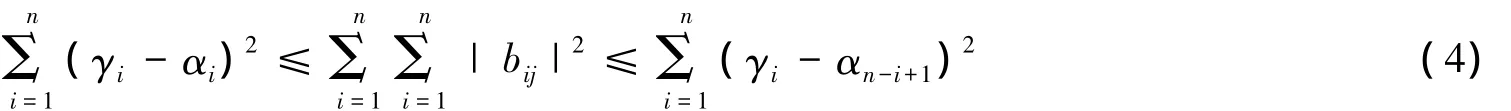
证明 由定理1和引理5,可知结论成立.


证明 定理2证明过程与定理1类似,此处略去.
推论3 在定理2的条件下,设B=(Bij)∈H(n,*),式(5)成立.

证明 由定理2和引理5,可知结论成立.

2.2 均值不等式在四元数矩阵上的推广
定理3 设A1,A2,…,Am(m≥2)为可交换的n阶四元数自共轭矩阵,则有Q(A)≥M(A)≥G(A)≥H(A).
证明 因为A1,A2,…,Am(m≥2)为可交换的n阶四元数自共轭矩阵,由引理1知存在n阶酉矩阵U,使得

由实数的均值-算术-几何-调和平均不等式,有

由此可知结论成立.
推论5 设A1,A2,…,Am(m≥2)为可交换的n阶四元数自共轭矩阵,则
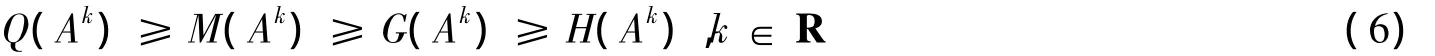
推论6 设A1,A2,…,Am(m≥2)为可交换的n阶四元数自共轭矩阵,则

2.3 Hölder不等式、Young不等式和Minkowski不等式在四元数矩阵上的推广

证明 由引理1和Hölder不等式可得,存在n阶酉矩阵U,使得
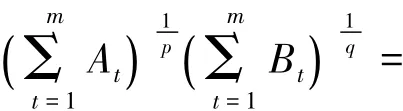

结论得证.

证明 由Young不等式和定理4的证明方法可得.

证明 由Minkowski不等式和定理4的证明方法可得.
[1]庄瓦金.体上矩阵理论导引[M].北京:科学出版社,2006
[2]陈香萍,伍俊良,李声杰.关于四元数矩阵迹的几个不等式[J].重庆工学院学报:自然科学版,2009,23(3):79-82
[3]WU J L,ZOU L M,CHEN X P,et al.The Estimation of Eigenvalues of Sum,Difference,and Tensor Product of Matrices Over Quaternion Division Algebra[J].Linear algebra and its applications,2008,428:3023-3033
[4]谢清明.四元数矩阵的范数与迹不等式[J].数学理论与应用,1999,119(2):38-39
[5]王松桂,吴密霞,贾忠贞.矩阵不等式[M].2版.北京:科学出版社,2006
[6]伍俊良,陈香萍,邹黎敏.2个四元数矩阵的同时对角化问题[J].云南大学学报:自然科学版,2009,31(3):222-226
[7]伍俊良,刘飞.实对称矩阵和与差的一些特征值与F-范数不等式[J].高等学校计算数学学报,2004,26(4):365-370
[8]刘静,耿宏瑞.一些数值不等式的矩阵形式推广[J].西南师范大学学报:自然科学版,2012,37(6):5-8

