巧用多项式的除法求矩阵多项式的逆矩阵
万 波
(重庆工商大学数学与统计学院,重庆 400067)
矩阵理论是线性代数的核心内容,有关矩阵的求逆是矩阵理论中的重点内容之一,也是各类线性代数考试中涉及较多的一类题型。在文献[1-2]中介绍了一类已知方阵A的二次或三次多项式方程,求方阵A的一次多项式的逆矩阵。文献[1-2]中的方法主要是通过观察构造从而得解,其方法灵活技巧性强不易被初学者掌握。文献[3-6]分别总结了几类特殊逆矩阵的求法。利用多项式的除法技巧,得到了一个所有已知方阵A的二次或三次多项式方程,求方阵A的一次多项式的逆矩阵结论,从而避开了需要观察构造才能得解这一麻烦过程。同时,利用多项式的除法技巧也可以得到最近文献[3]中的两个关于矩阵多项式的逆矩阵的结论。
1 主要结果
定理1 若n阶矩阵A满足A2+mA+nE=0,矩阵B满足B=A+kE,m,n,k满足km-n-k2≠0,记ω=km-n-k2,则矩阵B可逆,且B-1=ω-1[A+(m-k)E].
证明 利用多项式的除法有
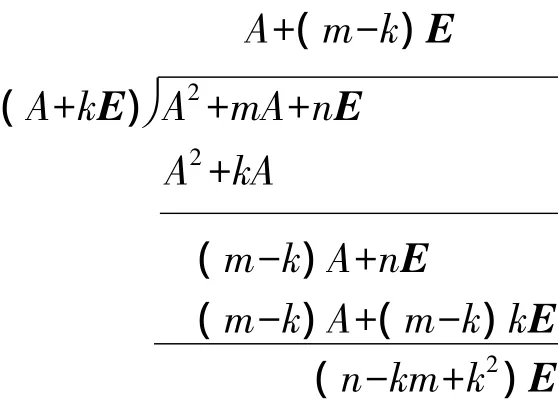
于是A2+mA+nE=(A+kE)[A+(m-k)E]+(n-km+k2)E=0,所以(A+kE)[A+(m-k)E]=-(n-km+k2)E,即(A+kE){ω-1[A+(m-k)E]}=E,因此矩阵B可逆,且B-1=ω-1[A+(m-k)E].
定理2 若n阶矩阵A满足A3+mA2+nA+lE=0,矩阵B满足B=A+kE,m,n,l,k满足l-nk+mk2-k3≠0,记ω=nk+k3-mk2-l,则矩阵B可逆,且B-1=ω-1[A2+(m-k)A+(n-mk+k2)E].
证明 利用多项式的除法有
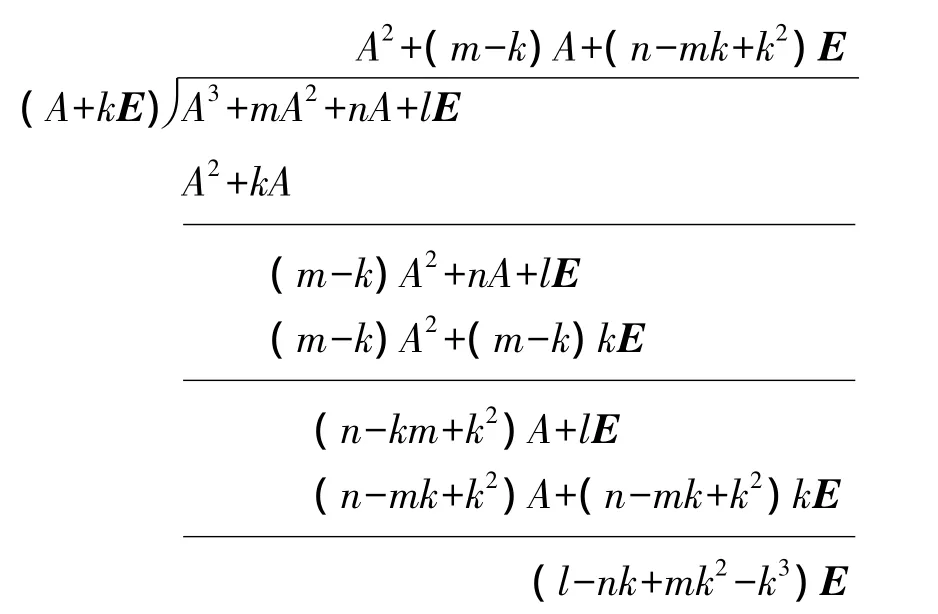
于是A3+mA2+nA+lE=(A+kE)[A2+(m-k)A+(n-mk+k2)E]+(l-nk+mk2-k3)E=0,即(A+kE){ω-1[A2+(mk)A+(n-mk+k2)E]}=E.因此矩阵B可逆,且B-1=ω-1[A2+(m-k)A+(n-mk+k2)E].
2 举例应用
下面举例说明上述两个定理的应用.
例1[1]设n阶矩阵A满足A2+3A-2E=0,证明A+E可逆,并求(A+E)-1.
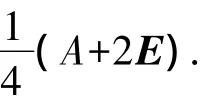
例2[1]设n阶矩阵A满足A3-A2+2A-E=0,证明E-A可逆并求其逆.
解 采用不同于文献[1]的做法,先求A-E的逆,直接利用定理2可知,这时m=-1,n=2,l=-1,取k=-1,计算得 ω=nk+k3-mk2-l=-1≠0,所以由定理2可知,A-E 可逆,且(A-E)-1=ω-1[A2+(m-k)A+(n-mk+k2)E]=-(A2+2E).因此E-A可逆,且(E-A)-1=(A2+2E).
3 推广应用
利用多项式的除法技巧,还可得到最近文献[3]中的两个关于矩阵多项式的逆矩阵的结论.
定理3[3]设n阶矩阵A满足A3-kE=0,矩阵B满足B=A2+mA+nE,m,n,k满足n3+k2+m3k-3mnk≠0,记d=n3+k2+m3k-3mnk,则B可逆,且有表达式:
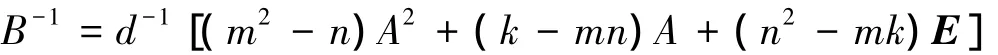
证明 将A3-kE=0两边分别同乘以(m2-n)A和(m3-2mn+k)得

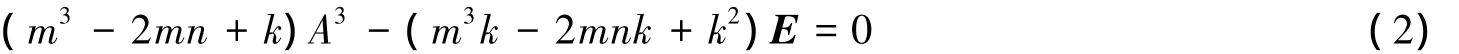
把式(1)+式(2),得
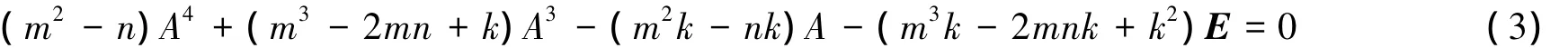
利用多项式的除法有,
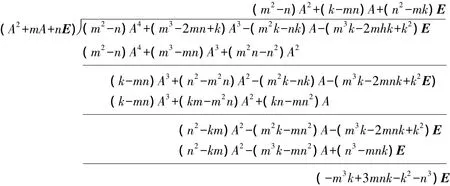
于是式(3)可以写成
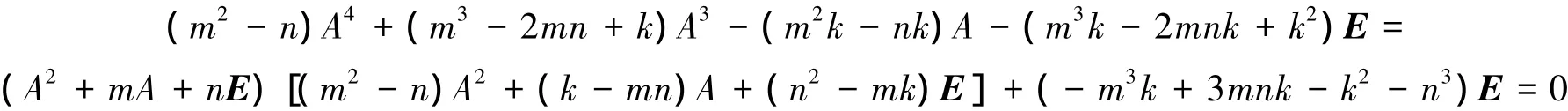
即(A2+mA+nE)[(m2-n)A2+(k-mn)A+(n2-mk)E]=(m3k-3mnk+k2+n3)E
因此B可逆,且有B-1=d-1[(m2-n)A2+(k-mn)A+(n2-mk)E].
定理4[3]设n阶矩阵A满足A3-mA2-nE=0,矩阵B满足B=A2+kE,其中m2k2+k3-2mnk+n2≠0,记 Ω=m2k2+k3-2mnk+n2,则B可逆,且B-1=Ω-1[-kA2+nA+(m2k+k2-mn)E].
证明 将A3-mA2-nE=0两边分别同乘以-kA和(n-mk)得
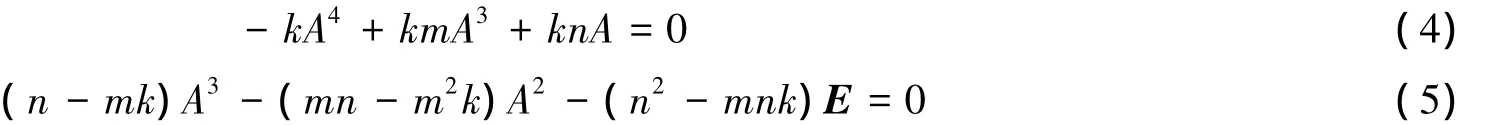
把式(4)+式(5)得
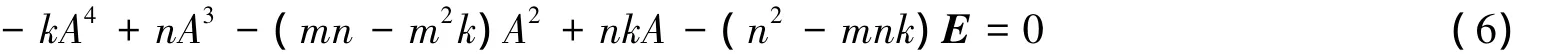
利用多项式的除法有
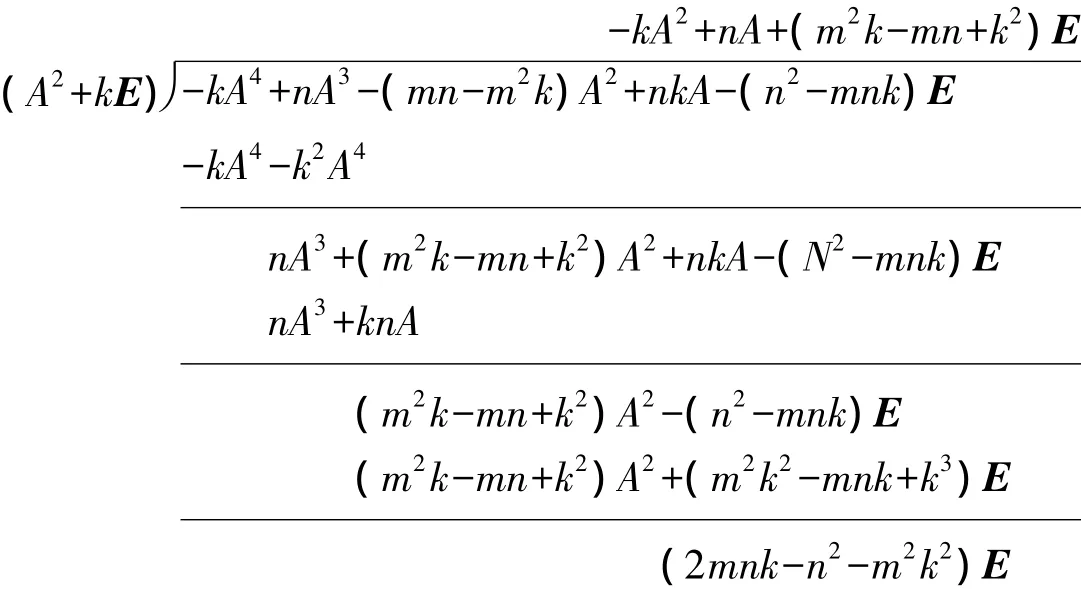
于是式(6)可以写成
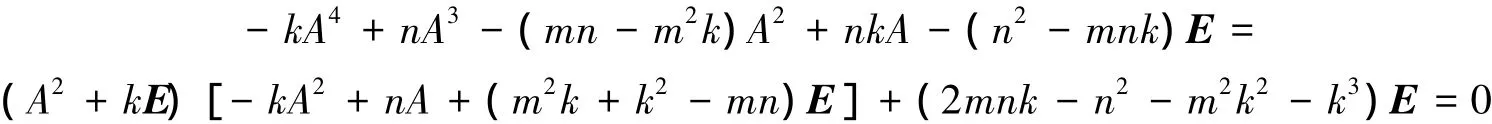
即(A2+kE){Ω-1[-kA2+nA+(m2k+k2-mn)E]}=E.
因此B可逆,且
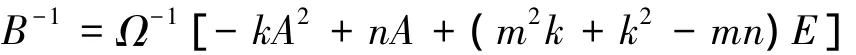
[1]袁晖坪,郭伟.线性代数[M].北京:高等教育出版社,2012
[2]北京大学数学系几何与代数教研室.高等代数[M].北京:高等教育出版社,2007
[3]赖新兴,肖清岚.两类矩阵多项式的逆矩阵的求法[J].江西理工大学学报,2013,34(3):90-92
[4]邵逸民.几类特殊矩阵的可逆性及其逆矩阵[J].通化师范学院学报,2008(12):5-6
[5]王美莲,何翠竹.一类特殊矩阵的逆矩阵的特点及求逆公式[J].忻州师范学院学报,2010,26(2):41-43
[6]蒋加清.关于循环矩阵求逆的一种快速算法[J].吉林师范大学学报,2011(1):88-90.

