若干双下标加权和的大数定律*
任春光,张 培,王学军
(1.郑州华信学院 基础教学部,郑州 451100;2.安徽大学 数学科学学院,合肥 230601)
在概率论中,大数定律是关于大量随机现象之平均结果稳定性的定理.不同的大数定律的差别只是对不同的随机变量(r.v.)序列而言,有的是相互独立的r.v.序列,有的是相依的r.v.序列,有的是同分布的r.v.序列,有的是不同分布的r.v.序列等等[1].此处对文献[2]中的Chebyshev大数定律、Markov大数定律、Bernoulli大数定律、Poisson大数定律和文献[3]中的Borel强大数定律进行了改进,即得到的是r.v.序列双下标加权和的大数定律.有关随机变量的其他一些性质,如最大值不等式和大偏差结果,可见文献[4],有关推广的Borel强大数定律的改进见文献[5],随机变量的Hájek-Rényi型不等式及其收敛速度见文献[6-7].随机变量序列的强收敛速度见文献[8],函数的一致联系性见文献[9-10].
令Ai,i=1,2,…为同一个概率空间(Ω,F,P)上的随机事件序列,记IA(ω)为事件A的示性函数,C,C1,c,ci,i=1,2,…为与n无关的常数,cni,ωni为实数列.
1 预备知识
引理1-6见文献[2],引理7见文献[3].
引理1(Chebyshev大数定律)[2]设{ξi},i=1,2,…是两两互不相关的r.v.序列,每一r.v.都有
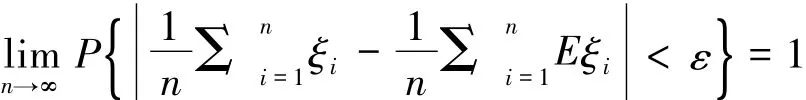

引理3(Bernoulli大数定律)[2]设μn是n次Bernoulli试验中事件A出现的次数,而p是事件A在每次试验中出现的概率,则对任意的ε>0,恒有
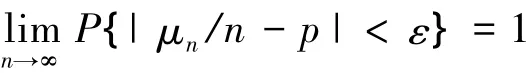
引理4(Poisson大数定律)[2]如果在一个独立试验序列中,事件A在第i次试验中出现的概率等于pi,以λn记前n次试验中事件A出现的次数,则对任意的ε>0,恒有

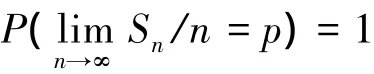
2 主要结论
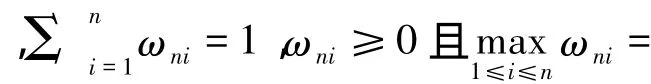
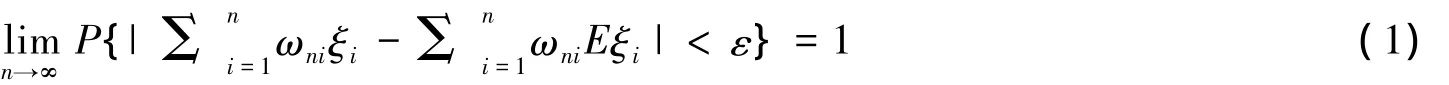

对任意的ε>0,再由Chebyshev不等式,可得
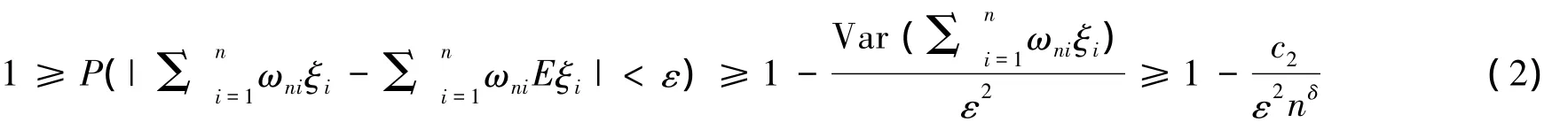
于是,在式(2)中,令n→+∞得式(1),因此命题得证.

其实,Markov大数定律、Bernoulli大数定律、Poisson大数定律和Borel强大数定律中也可以进行类似的改进.
定理2(Markov大数定律的改进) 若{cni}为双下标常数序列,{ξi},i=1,2,…为一均值为零的r.v.序列,且满足
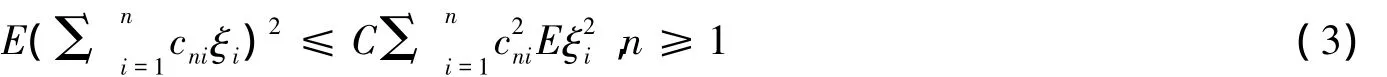
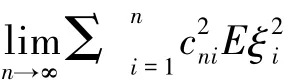
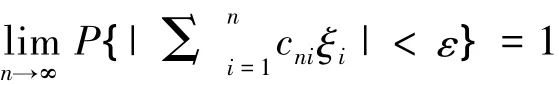
证明 显然有
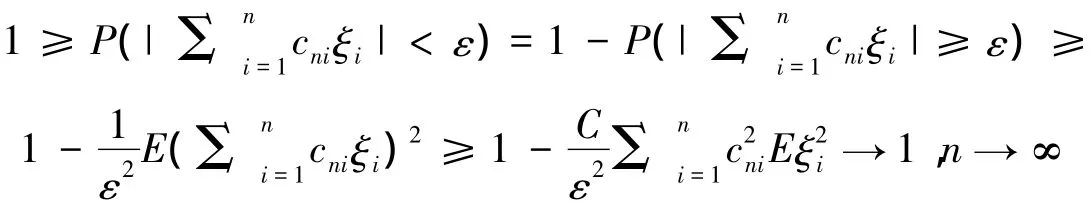
注2 对{ξi},i=1,2,…为均值为零的两两互不相关的r.v.序列、鞅差序列、均值为零的NA序列、均值为零的φ-混合序列(混合系数满足一定系数)等,都满足式(3).进一步,若≤C1i,i≥1,取cni=,则可以验证
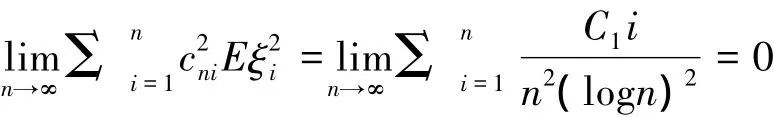

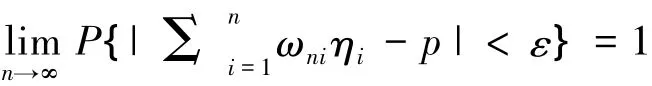
证明 易知Eηi=p,Dηi=pq≤1/4,而
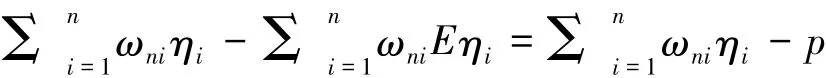
从而由定理1即可推出定理3.


证明 易知Eαi=pi,Var αi=piqi≤1/4,而

从而由定理1即可推出定理4.




对∀ε>0,由 Chebyshev不等式得
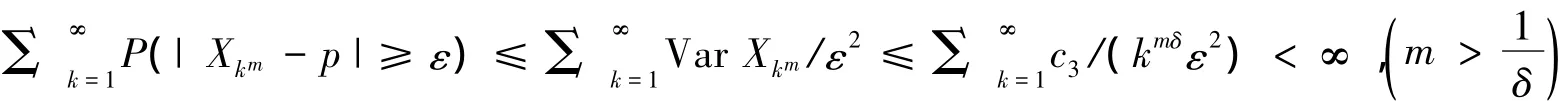
从而

下面用子序列的方法来证明定理5的结论.因为对 ∀n∈N+,∃k=k(n)∈N+,满足不等式km≤n<km+kδ,所以
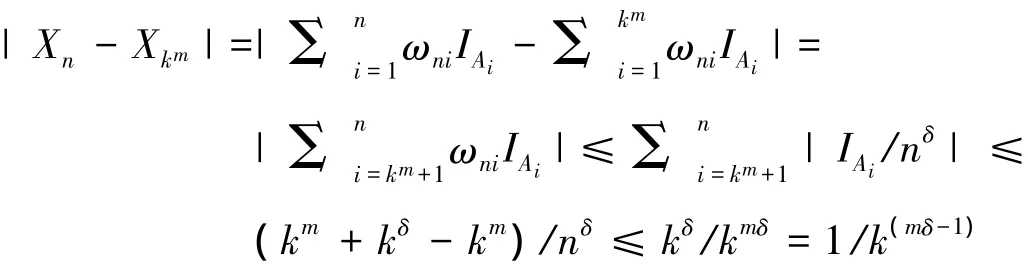
于是
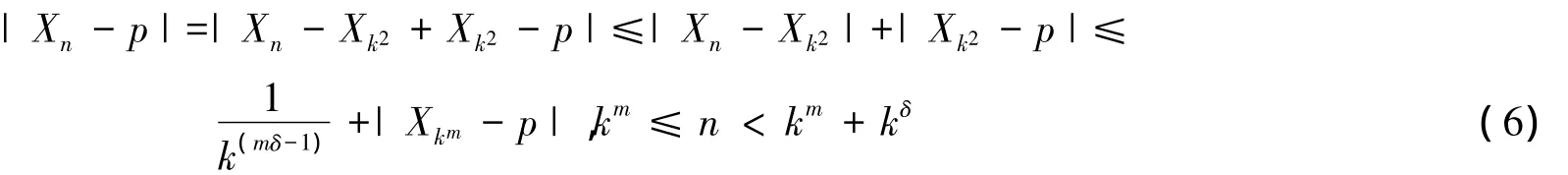
式(6)中令n→+∞ (注意到n→+∞时,k→+∞),再利用式(5)得式(4),因此命题得证.
3 结束语
双下标r.v.序列和的大数定律及r.v.序列加权和的大数定律都有很多研究成果,r.v.序列双下标加权和的结果并不常见,另外在相依情形下的r.v.序列加权和的大数律问题是值得研究的,在今后科研中将关注此类问题.
[1]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2004
[2]李贤平.概率论基础[M].北京:高等教育出版社,1997
[3]LOÈVE M.Probability Theory I[M].4th Edition.Beijing:Spring-Verlag,2000
[4]李晓琴,胡舒合,王学军,等.M-Z型序列的最大值不等式和大偏差定理[J].安徽大学学报:自然科学版,2010,34(3):5-9
[5]任春光,胡舒合,李旭,等.一个推广的Borel强大数定律的改进[J].安徽大学学报:自然科学版,2011,35(3):25-28
[6]赵婷,胡舒合,李晓琴,等.一类随机变量的概率不等式及几乎处处收敛性[J].安徽大学学报:自然科学版,2010,34(1):7-10
[7]胡舒合,胡晓鹏,张林松.二阶矩限制下的Hajek-Renyi型不等式及其应用[J].应用数学学报,2005,28(2):227-235
[8]胡舒合.强大数定律的若干新结果[J].数学学报,2003,46(6):1123-1134
[9]费时龙,占伟军.函数一致连续性的几个判别方法及其应用[J].重庆工商大学学报:自然科学版,2013,30(8):1-3
[10]刘倩,任晓花.观察法判断一元函数的一致连续性[J].重庆工商大学学报:自然科学版,2013,30(7):9-11

