Glodstein条件下的一种修正CD共轭梯度法

黎小林

（重庆师范大学数学学院，重庆 401331）

1 引言

考虑无约束优化问题

其中Rn是n维欧几里得空间，f:Rn→R是一个连续可微的函数［1］.

众所周知，共轭梯度法是求解该类问题的一种重要方法，它具有如下的迭代格式

其中αk是某种线搜索下的步长，dk满足

其中βk是共轭参数，不同的βk的取法会产生不同的共轭梯度法，常见的βk有如下定义

对应的方法分别叫做 FR（Fletcher-Revees），PRP（Polak-Ribiere-Polyak），HS（Hestenes-Stiefel），LS（Liu-Storey），CD（Conjugate Descent）和DY（Dai-Yuan）共轭梯度法.

共轭梯度法是求解大规模无约束优化问题的一种方法，它存储量小、计算简单.该方法由Hestenes和Stiefel在求解对称正定线性方程时提出，并由Fletcher和Revees在求解无约束极小化问题中发展起来，它在控制论、工程、管理科学和优化研究中有广泛应用.

受文献［2］启发，主要对 Conjugate Descent法进行了修正，得到了一个新的修正 Conjugate Descent（MCD）算法，并证明了新算法在一个Goldstein线搜索准则下的全局收敛性.

采用的Glodstein线搜索准则［3］为

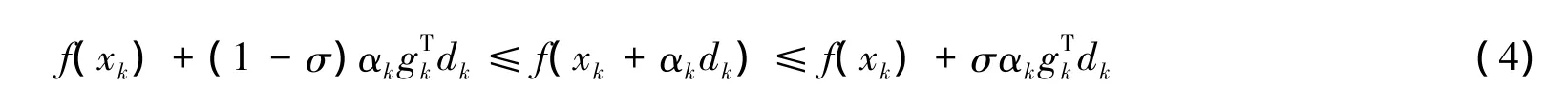
戴彧虹（文献［4］）对非线性共轭梯度法的收敛性进行了分析，并且在文献［5］中提出了一种具有强全局收敛性的共轭梯度法.另外，张丽等提出了几种3项共轭梯度法（文献［6，7］），它们在不依赖任何线搜索的条件下满足充分下降性，同时在适当条件下也具有较好的全局收敛性，这些在文献的数值算例中得到很好的体现.

2 算法

给出的MCDCG算法［6］的迭代格式为式（2）和

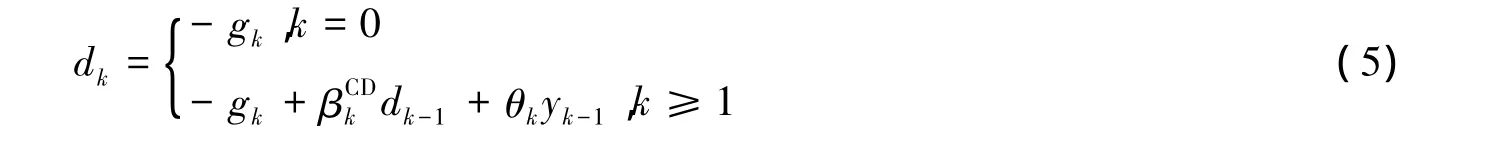
其中

显然，由式（5）（6）和βCD的公式知，对于任意的k≥0，有

MCDCG 算法:初始步:给定 x0∈Rn，ε≥0，令 d0=－g0，k:=0.

第1步:若‖g0‖≤ε，则停止.

第2步:求出满足Glodstein准则的步长αk.

第 3 步:计算 xk+1=xk+αkdk，若‖gk+1‖≤ε，则停止.

第4步:通过式（5），求得dk+1;令k:=k+1，转第2步.

3 MCDCG算法的收敛性

作如下假设［4］:

（A）水平集Ω={x∈Rn|f（x）≤f（x0）}有下界，其中x0∈Rn为初始点.

（B）f在水平集Ω的一个领域N内连续可微，且其梯度g满足Lipschitz连续，即存在常数L＞0，使得

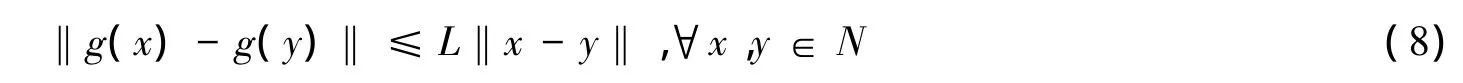
显然，在上述假设下，存在某个γ1＞0，使得

引理1 如果存在常数ε＞0，使得‖gk‖≥ε对任意k≥0成立，则必存在常数M＞0，使得‖dk‖≤M对任意k≥0成立.

证明 当k=0时，‖d0‖=‖－g0‖=‖g0‖≤γ1，此时令 γ1=M，结论成立.

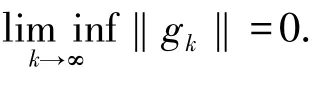
证明 用反证法.假设定理1的结论不成立，则存在常数ε＞0，使得‖gk‖≥ε对任意k成立.下面分两种情况进行讨论.

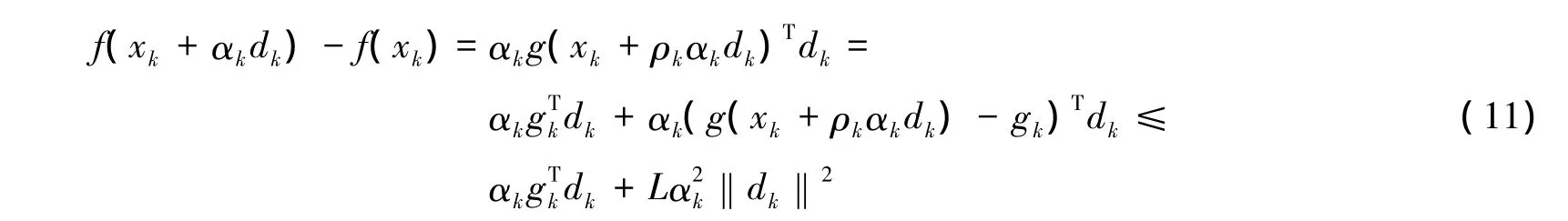
由式（11）和式（4）的左边不等式知，当k∈Κ充分大时，有

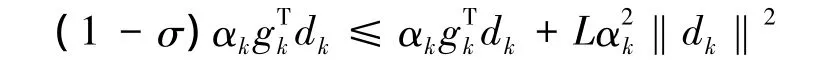
整理可得

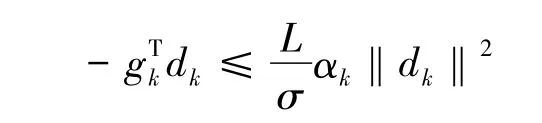
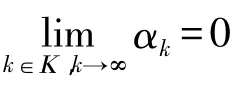
［1］张霞.一个新的光滑低阶精确罚函数［J］.重庆工商大学学报:自然科学版，2013，30（8）:15-18

［2］ZHANG L，ZHOU W J，LI D H.A Descent Modified Polar-Ribiere and Polyak Conjugate Gradient Method with Armijo-type Line Search［J］.IMA Journal of Numerical Analysis，2006（26）:629-640

［3］孟继东，杜学武.Armijo型线搜索一个修正LS共轭梯度法的全局收敛性［J］.重庆师范大学学报:自然科学版，2012（6）:6-8

［4］DAI Y H.Convergence Properties of Nonlinear Conjugate Gradient Methods［J］.SIAM Journal on Optimization，1999（10）:345-358

［5］DAI Y H，YUAN Y.A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property［J］.SIAM Journal on Optimization，1999，10（1）:177-182

［6］ZHANG L，ZHOU W，LI D.Some Descent Three-term Conjugate Gradient Methods and Their Global Convergence［J］.Optim Methods Softw，2007（22）:697-711

［7］ZHANG L，ZHOU W，LI D.Global Convergence of a Modified Fletcher-reeves Conjugate Gradient Method with Armijo-type Line Search［J］.Numerische Mathematik，2006（104）:561-572