网络化环境下双电机的同步控制研究*

许 强，陈其工，葛 愿，曾 晗

(安徽工程大学电气工程学院，安徽芜湖 241000)

随着网络通信技术和计算机技术的高速发展，网络控制系统(Networked Control Systems，NCSs)应运而生。NCSs是一种全分布式、网络化实时反馈的控制系统，主要特征是通过网络来实现控制系统各部分信息交换［1］。结合了控制和网络的优势，特点就是具有控制范围广、系统连线少、适应能力强、运行成本低等。但同时由于多个数据包在网络中，发送信息时候要分时复用网络通道，由于网络通信带宽的承载能力是有限的，这样就会导致信息冲突，重传等现象发生。信息在传输过程中，就不可避免地存在着通信延迟，数据包丢失，数据包的时序错乱度等方面的问题。

目前，国内外众多学者在网络化环境下电机控制系统取得一系列成就，研究工作都主要集中在网络环境下单电机控制进行研究，却很少涉及多电机运动控制系统［2］，同时随着现阶段工业以太网或现场总线的理论研究逐步深入，利用网络化控制系统平台使多轴运动系统同步控制，是一个重要的研究课题。在此将研究网络化环境下双电机系统实现同步控制问题，对多轴运动系统网络化控制具有一定理论参考价值。本文以两台直流伺服电机为研究对象构造一个网络化控制系统，并考虑系统具有时变短时延，首先将系统建模成一个切换系统，然后通过求解一组线性矩阵不等式约束的多目标优化问题［3］，采用状态空间反馈控制方法，实现双电机的同步控制。最后基于truetime工具箱对此模型进行仿真实验，验证本文方法的有效性和优越性。并可推广多台电机之间实现同步控制。

1 双电机的NCSs建模

在对双电机的网络化控制系统进行实物仿真之前，需要对系统的各个部分进行数学建模，这样才能比较正确地反应整个控制系统的特性。首先建立直流伺服电机的数学模型，其次建立具有时变短时延的网络化控制系统模型。

通过对渔民CP电镜下电切术患者进行有针对性知识宣教，有效改善了渔民患者的治疗依从性，减少了术后并发症，降低了术后复发率，值得临床进一步推广。

1.1 直流伺服电机的数学建模

首先从使用机理建模的方式来建立其电机的数学模型。设直流电机的电压输入ua，电机在此控制电压作用下产生的反电动势为ea，其动态运行过程满足如下方程。

本次采样地点露头新鲜，剖面岩石发育良好，按照不同岩性变化采取等间距采集样品，在地层分界处(图2a)则加密采样，共采集硅质岩、泥质硅质岩、硅质泥岩样品15件，其中采集上泥盆统6件，下石炭统9件，样品产出地质剖面图见图3。

电机的电压平衡方程式:

ia为电枢中产生的控制电流(A)，Ra为电枢回路总等效内阻(Ω)，La为电枢电感(H)。

电枢电动势方程式:

本文提出了一种移动自组织网络(机会网络)的多节点间链路预测方法,采用模式分类方法,将链路预测问题转换成模式分类问题,借助CNN在特征提取上的优势提取图像特征,以期抓取出相邻节点、多个节点甚至局部网络拓扑动态演化的规律.本文的主要贡献包括:①将预测问题转换成模式分类问题,利用深度学习模型来实现多节点间的链路预测;②应用混沌时间理论解决网络切片的问题;③使用图像数据来表示网络的结构特征.

电机转矩平衡方程式:

T为电机运行过程中产生的电磁转矩(N·m)，J为电机转子的转动惯量(N·m·s2)，B为黏性阻尼系数(N·m·sec/rad)。

电磁转矩方程式:

Kt为转矩系数。

为实现对夜间运动车辆的识别，引入新的色彩空间和模糊理论来解决这一问题。基于新的色彩空间和模糊集理论的跟踪模型包括帧色彩处理和背景剔除两个环节。首先，利用初始识别结果，获取前景和背景的色彩信息，并间初始视频帧处转换为新的色彩空间HSrg，其中HS 为HSV 中的两个图层，r 和g 分别为RGB 图层中的对应的R 和G 图层标准化后的图层，即有r=R/( R+ G+B )和g=G/( R+ G+B)。为了减轻图像中噪声的影响，分别对识别目标在HSrg 色彩空间中每个图层使用中值滤波，得到滤波后的值分别为：

由式(1)、式(2)、式(3)、式(4)得到直流伺服电机控制系统完整的数学模型:

综上所述，在社会经济发展的推动下，土木工程行业迈入了快速发展的阶段，在整个施工过程中，面临着机械设备的使用和人员管理的复杂性。若管理工作不到位，不仅会出现施工质量问题，还可能会引发重大的安全事故，甚至造成人员伤亡。为了更好地保证工程的施工质量，必须重视土木工程施工管理工作，保证工程的顺利进行，推动土木工程建设行业的长远发展。

内部控制制度通常需要管理层进行决策，但是管理层又不会花费太多的精力在内部控制制度上，而内部控制负责人又不能够越过管理层进行制度的优化，而且管理层根本不了解医院内部管理的实际情况，往往会提出或者作出不符合医院内部控制发展的决策，而内部控制负责人因为级别较低，往往提出的建议也不会被采纳。

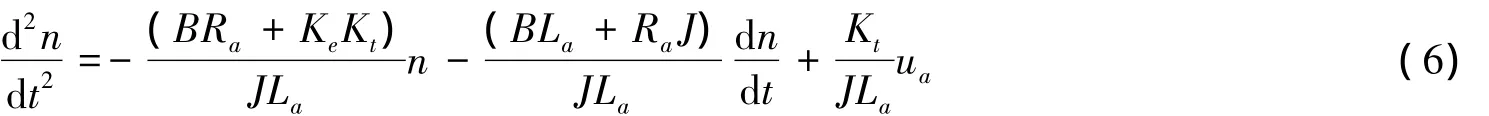
选取状态变量:x1=θ，x2=n，x3=，根据式(6)写成状态方程空间形式:

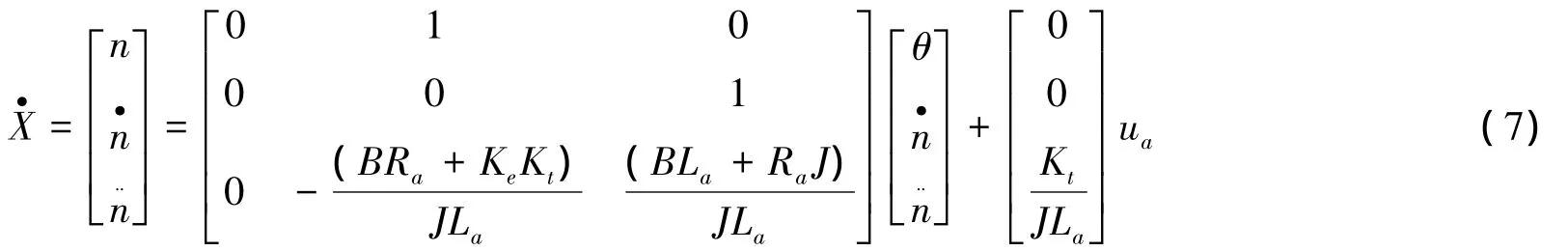
假定系统的输出为转轴的转角，电机的负载为常数，则系统的输出方程为

Development of Chinese cosmetic industry in condition of globalization 7 6

（3）模具检验 按时对模具进行定期检验，保证铸造毛坯的外形无尖角及毛刺，铸件转角处适当增加铸造圆角，避免模具上尖角位导致的应力产生。

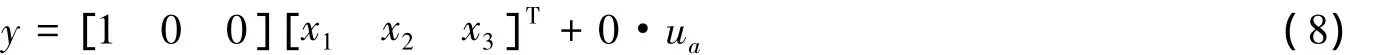
令:

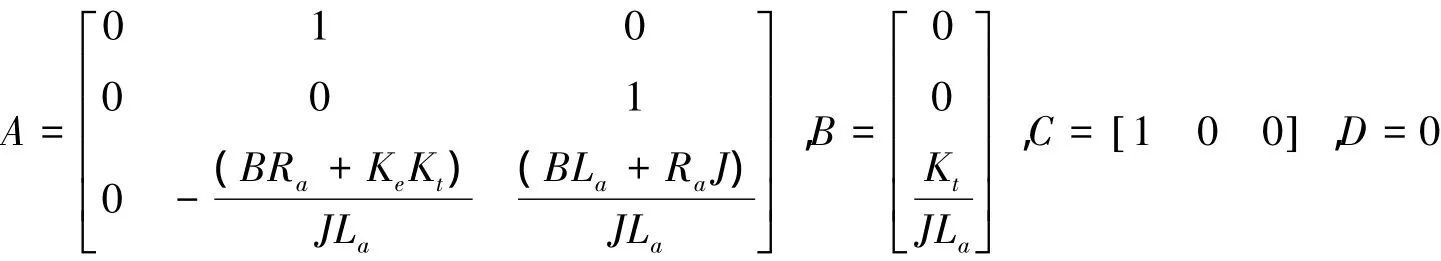
则根据式(7)、式(8)。直流伺服电机的状态空间方程可表示为

1.2 时变短时延的NCSs的数学建模

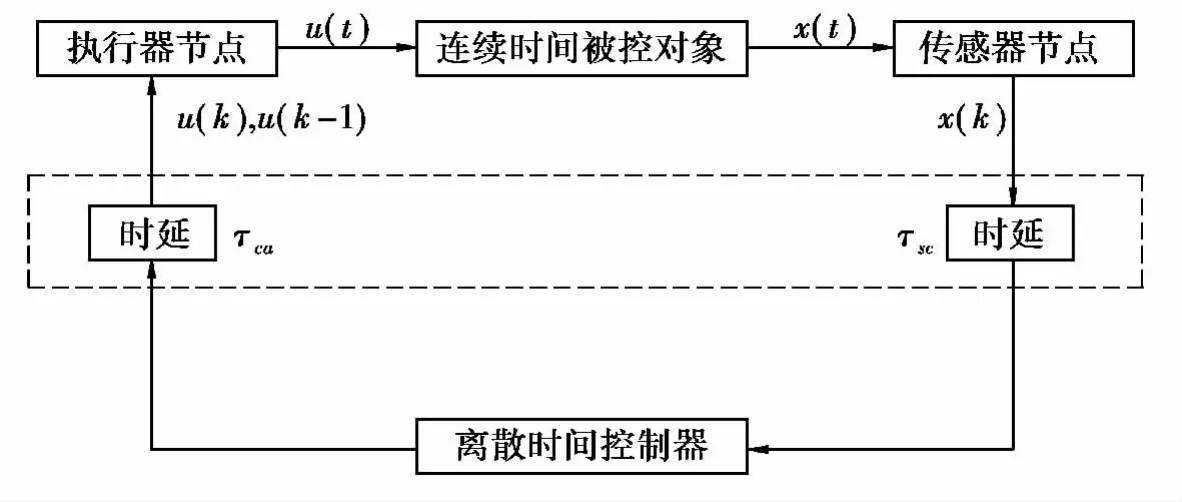
图1 具有时变短时延的NCSs结构

图1是一个典型网络化控制系统的框图，网络传输的时延主要是指从传感器到控制器的时延τsc和从控制器到执行器的时延τca，该两个时延都是随机的且都小于一个采样周期T，网络产生的诱导时延表示为τk=τsc+τca［4］。图1中的连续时间被控对象可有如下的状态空间模型描述:

其中，u(t)∈Rn和u(t)∈Rn分别表示系统状态和输入，Ap和Bp是两个定常矩阵。对于所研究的NCSs，为了研究方便，做以下假设:

DC1、DC2是转角状态响应曲线。当网络模型采用上述无时延情形下的状态反馈系数时，系统的动态性能明显变差，显然达不到系统所要求的控制性能。因此，根据时变短时延特性，建模成切换系统，应用线性矩阵不等式求解稳定化状态反馈控制器［8］。

假设2:传感器数据和控制量都是采用单包传输模式，且数据包都带有时间戳，不考虑数据包丢失和时序错乱的影响;

由式(16)两边同乘P-1，可得到:

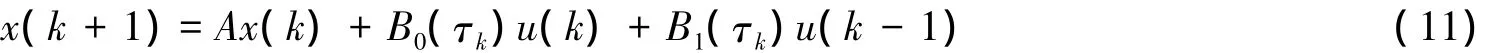
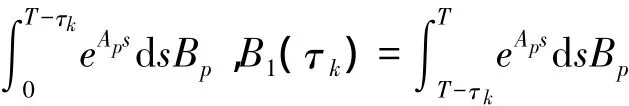
（一）正确认识情感态度价值观目标。情感态度与价值观，是人对亲身经历过事实的体验性认识及其由此产生的态度行为习惯。它对人一生的成长都有着举足轻重的作用。英语教师在制定英语课目标时，还应意识到英语本质上是一种语言，而不同于一般知识，英语学习的目标首先要关注语言的交流功能，即作为人们交流思想感情的工具，所以英语学习首先要包含情感态度方面的目标和社会文化方面的知识。

根据假设1，执行器采用的是时间驱动模式，设定其读取缓冲区的周期为T0，且使其满足T0=T/N(N为自然数)。根据假设2、3可以推定当前的控制量为u(k)在经过τk时间滞后到达执行器端。那么对任意的k＞0，记u(k)和u(k-1)作用在被控对象上的时间分别记为n0(k)T0和n1(k)T0，则有:

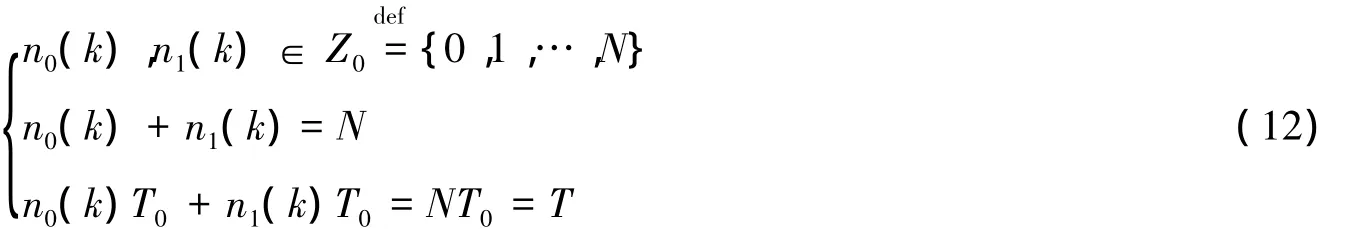
从式(12)中可以看出n0(k)，n1(k)均在有限集合内取值，因此，可将NCSs视为一个具有有限个子系统的切换系统。令如下关系成立:

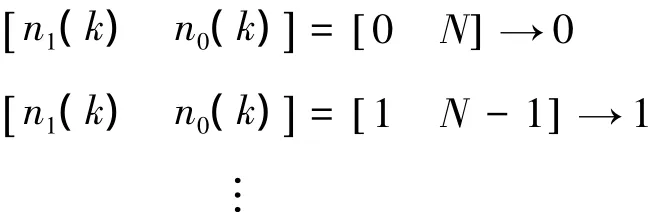
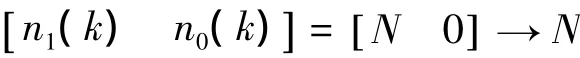
结合式(11)、式(12)可将NCSs写成如下的切换系统模型:

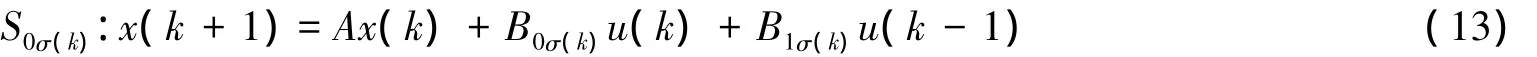
2 无时延情况下双电机的同步控制

2.1 状态反馈控制增益求解

根据建立的状态空间式(9)，先判定系统是否为可观、可控。若可观、可控则根据状态变量反馈控制规律，有:

K为1×3的状态反馈增益向量。

其中，Pj＞0 和Qj＞0 是待定矩阵。记 η(k)=xT(k)[，则式(21)可得:

考虑系统的状态空间模型式(9)在状态反馈式(14)作用下，使得闭环系统:

考虑Lyapunov函数V=xTPx，由Lyapunov稳定性理论可知，系统式(15)是渐进稳定的，得到以下不等式:

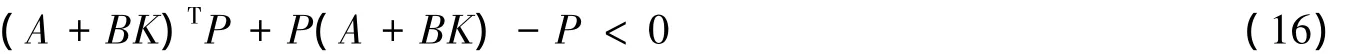
其中式(16)有可行解P＞0，其中P=PT。

假设3:网络时延为时变短时延，即时延满足小于一个采样周期:τk≤=eT≤T，其中0≤e≤1。由于 τk≤T，基于以上假设，那么可以推定任意一个采样周期 [kT(k+1)T]内最多只有两个控制量u(k)和u(k-1)能作用在被控对象上。故将系统式(10)以采样周期T离散化，可得到离散NCSs模型:

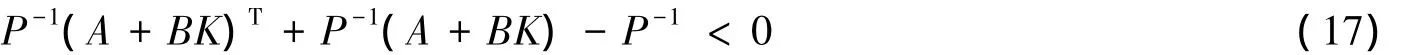
令X=P-1，Y=KP-1。则式(17)可重写为

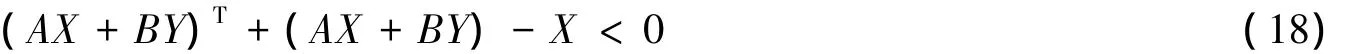
因此，若以下线性矩阵不等式:

引理1［11］对任意矩阵A，P＞0和Q＞0，不等式ATQA-P＜0成立，当且仅当存在一个矩阵，Y，使得以下矩阵不等式成立:

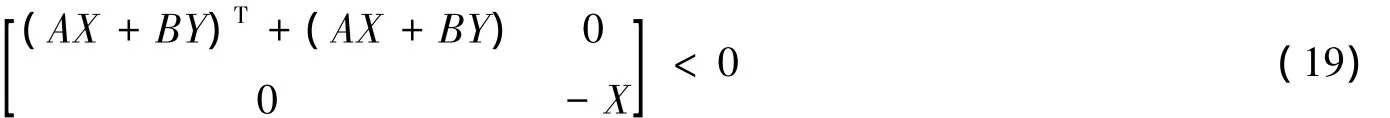
成立，那么系统式(15)渐进稳定，那么所设计的状态反馈控制器增益为K=YX-1。针对式(19)是一个线性矩阵不等式，可以应用Matlab中的LMI工具箱feasp求解器来求取解(X，Y)。

2.2 仿真及结果分析

采用两个相同信号的直流伺服电机进行本次仿真，在Simulink上建立双电机的同步控制模型，模型选择同步控制策略是采用给予同一控制信号并补偿同步误差［6］。用Simulink里面的S-Function模块编写该同步控制策略代码，在选取合适的使得两个相同直流电机在相对误差小于5%情况下实现双电机的同步控制。为验证本文给出的控制方法的有效性，对系统式(9)进行仿真。电机参数为［7］电感La=0.24×10-3H;等效电阻Ra=2.18 Ω;转矩系数Kt=23.4×10-3Nm/A;转动惯量J=10.3×10-3N·m·s2;黏性阻尼系数B=2×10-5N·m·sec/rad;反电动势系数Ke=2.171×10-2V·sec/rad;

电机参数带入式(7)中，计算出等价数学模型，然后再基于该模型，利用式(19)的定理求取状态反馈控制器。利用Matlab中LMI工具箱的feasp求解器进行求解，可分别求得该控制系统的两个状态反馈增益阵:K1= [ 1.000 1.382 0.249]、K2= [ 1.000 1.671 0.312]。在给定的仿真条件下，采用所设计的控制器，双电机的同步控制状态轨迹响应如图2所示。系统设计要求的动态特性性能指标:给单位阶跃信号r输入电压激励直流电机，两个状态响应曲线分别为两个电机的转角响应，要求当转角稳定变化时，其状态响应曲线的调整时间应小于10 s，超调量小于20%，稳态误差小于4%。该系统设计的参数满足系统稳定的要求。在此搭建的Simulink仿真平台上应用TrueTime工具箱，加入网络化环境，建立双电机控制系统在网络下的同步控制，网络参数设置为网络类型为CSMA/CD(Ethernet);最小数据帧长度为512 bits;数据发送率为10 Mb/s;丢包率为0;传感器、控制器、执行器计算时间分别为0.3 ms、0.5 ms、0.3 ms;仿真时间为15 s。仿真状态响应曲线如图3所示。

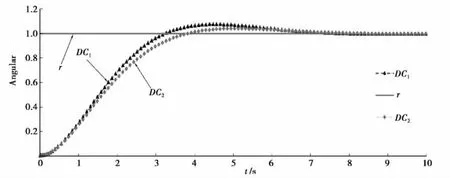
图2 无时延条件下双电机的同步控制

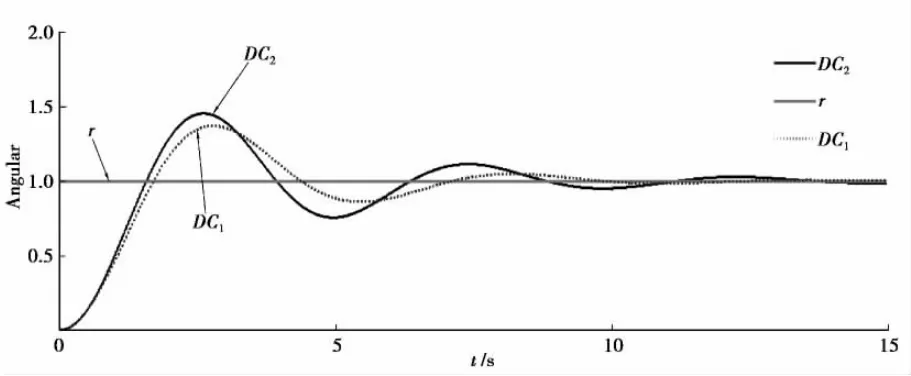
图3 随机时延条件下双电机的同步控制1

假设1:传感器和执行器均采用时间驱动模式，控制器采用事件驱动模式，其采样周期为T;

3 有时延情况下双电机的同步控制

3.1 稳定化状态反馈控制器设计

式(13)中所建立的是一个具有有限个子系统的离散时间切换系统的模型，将时延的变化转化为系统模型之间的切换，来借助切换系统理论和方法来设计稳定化控制器。那么网络时延的变化速率在一定程度上决定了切换信号σ(k)的切换速率，而切换信号的的切换速率是由其平均驻留时间ta来反映［9］。考虑设计的状态反馈控制器u(k)=Kx(k)，由切换系统式(13)可得到一下闭环NCSs模型:

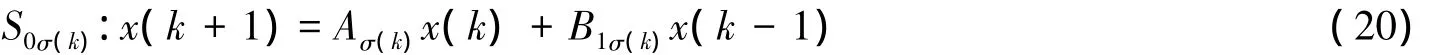
本小节的目的是设计一个形如u(k)=Kx(k)的状态反馈控制器，使得闭环NCSs(20)指数稳定，同时建立NCSs的指数衰减率ρ与最大允许时延上界和反映时延变化率λ的平均驻留时间ta之间的定量关系［10］。

定理1 考虑系统(20)，若存在正标量 λ＜1，μ≥1 和适当维数的矩阵Pj＞0，Qj＞0，j=0，1，…，N，使得以下不等式:

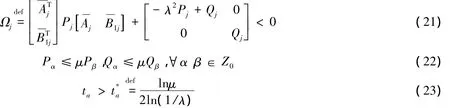
成立，则系统式(20)指数稳定并具有指数衰减率ρ(λ，ta)=。

何西，二十五岁，骨科医生，是二叔何守二的儿子。电话铃嚎了半天，何西也没接。何东知道他在当班，就急忙往医院赶。何西刚跟着主治医做完手术，正洗手呢，一看见何东，一把把他揪到走廊里的光荣榜前面，指着一大胖脸，鱼泡眼的大幅照片问何东：“认识他吗？”

证明 令k1，k2，…，ki，i≥1 表示 σ(k)在间隔［0，k)内的切换点，且ki是递增排列，ki＜k。系统式(20)的子系统模型为

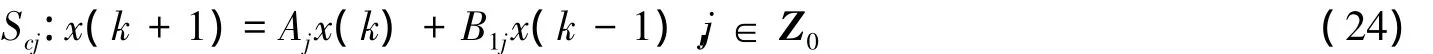
为系统式(20)选取如下的Lyapunov函数:

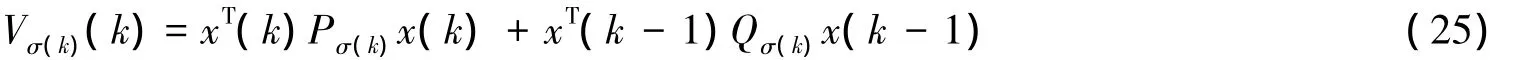
通过改变K可以改善系统的稳定性、快速性及稳定误差。在实际工程中求反馈向量K有许多方法，比如要满足要求的动态特性要求，可以极点配置方法确定系统的闭环极点，再通过Ackermann公式计算K。随着现代控制学发展，控制问题往往有很多限制以及附加条件，其实大多都可以转化为线性矩阵不等式条件，这样就可以利用线性矩阵不等式来求解［5］，本文利用线性矩阵不等式来求解K。

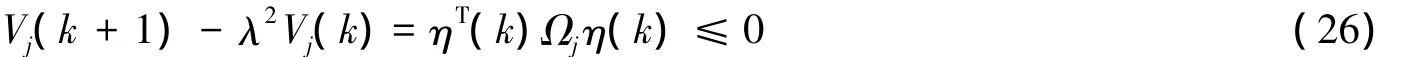
由式(26)可得:

由于系统式(20)的状态在切换点不跳变，由式(22)可得:

由式(27)和式(28)可以递推求得:

ea为电机的反电动势(V)，Ke为反电动势常数，θ为电机的转角(rad)，n为电机的转速(rad/sec)。

由式(29)可得

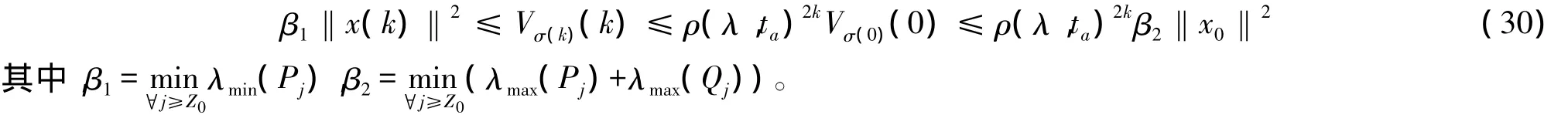
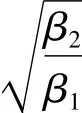
他被吓得激灵一哆嗦，手掌触电般地缩了回来。他的心“咚咚”地跳着，满面通红地扭头望向门口，正瞧见青萝那张气势汹汹的脸。

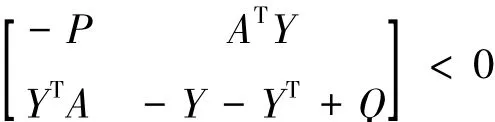
以下定理给出了稳定化状态反馈控制器u(k)=Kx(k)的一个设计方法。

定理2 对于给定的正标量 λ＜1 和 μ≥1，若存在适当维数的矩阵X，V，Rj＞0 和Sj＞0，j=0，1，…，N，使得式(23)和以下的线性矩阵不等式:

综上所述，当采用基于信号概率的功耗计算模型进行MPRM电路的功耗计算时，本文所提出的基于概率表达式的MPRM电路功耗计算方法能够在合理的时间内获得准确的电路功耗计算结果.

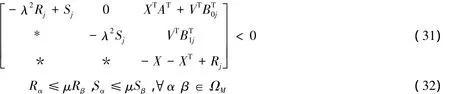
成立，则控制器u(k)=VX-1x(k)将保证闭环NCSs(20)指数稳定并具有指数衰减率ρ(λ，ta)=。

证明 由引理1可知，Ωj＜0成立当且仅当存在一个矩阵Y，使得以下不等式:

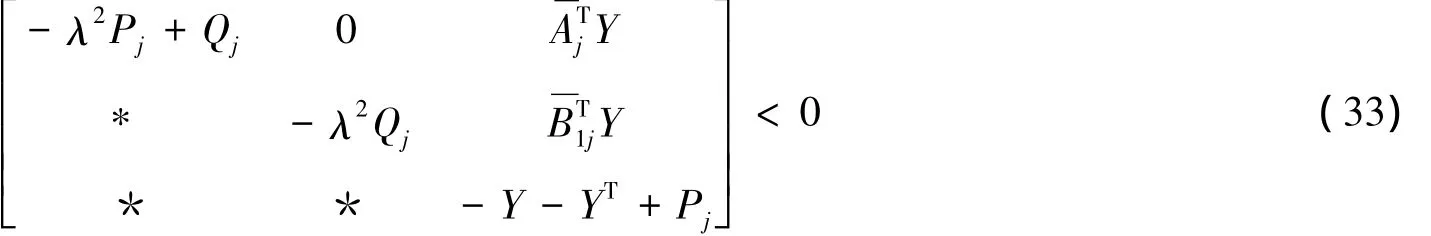
成立。从以上不等式可推出矩阵Y是可逆的。对以上矩阵不等式分别左乘矩阵diag{Y-T，Y-T，Y-T}和右乘矩阵 diag{Y-1，Y-1，Y-1}，可得:

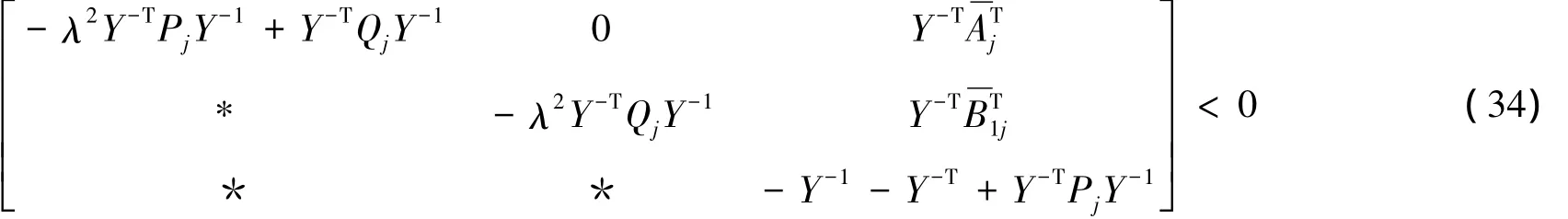
记X=Y-1，V=KX，Rj=XTPjX，Sj=XTQjX，则由以上不等式可得矩阵式(31)。对Pα≤μPβ和Qα≤μQβ都分别左乘矩阵XT和右乘矩阵X既得矩阵式(32)，从而，由定理1可知定理2成立。证明完毕。

那么在设计控制器时，要保证线性矩阵不等式(LMIs)式(31)和式(32)可行的情况下，μ应该尽量取小以获取一个小的指数衰减率ρ(μ，ta)，这样也使得条件式(23)更容易得到满足。

“坚持让数据多跑路，让患者少跑路，努力实现院内流程‘最多跑一次’，看病就医少跑一次。”马胜林这样理解公立医院的“最多跑一次”。

3.2 仿真及结果分析

本课题研究的只考虑网络诱导时延的影响，并且假设网络的诱导时延都是短时延，丢包率对系统性能的影响可忽略不计。该双电机网络化控制系统，采样周期取为T=10 ms，将采样间隔分为十等分，即令N=10，从而执行器读取缓冲区的周期便为T0=1 ms。通过计算可知该网络最大允许网络诱导时延上界为=4T0=4 ms，可知，时延只有 5 种取值可能，即 τ(k)∈{0，1，2，3，4}ms。系统的模型可由式(20)描述，那么可知该系统式(20)最多包含5个子系统。将这5个子系统用Sci，i=0，1，2，3，4表示。Sci的系统矩阵由n1(k)和n0(k)决定，根据之前论述的切换系统知识可知，［n1(k)n0(k)］只有5种可能取值分别是［0 10］，［1 9］，［2 8］，［3 7］，［4 6］。

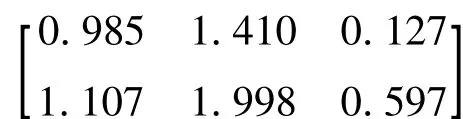
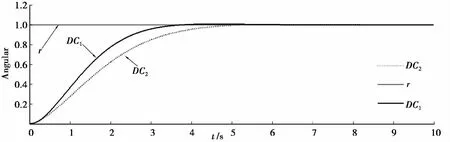
图4 随机时变时延情形下双电机的同步控制2

仿真利用TrueTime工具箱进行研究，网络参数设置如下:网络类型为CSMA/CD(Ethernet);最小数据帧长度为512 bits;数据发送率为10 Mb/s;丢包率为0;传感器、控制器、执行器计算时间分别为0.3 ms、0.5 ms、0.3 ms;仿真时间为12 s。仿真结果如图4所示。

仿真结果符合系统所要求的动态特性的性能要求，表明所设计的稳定化状态反馈控制器的有效性，该双电机系统在网络环境下实现了同步控制。

4 结论

介绍了具有随机短时延网络化控制系统建模与设计问题，实现了双电机系统在该环境下同步控制，其中涉及双电机同步控制采用给予同一控制信号并补偿同步误差控制策略、并且该策略可以适用更多的电机同步控制。将离散化后的网络化控制系统建模成一个具有有限个子系统的离散时间切换系统的模型，将时延的变化转化为系统模型之间的切换，再采用线性矩阵不等式方法求出稳定化状态反馈矩阵控制器。仿真结果验证本文方法的有效性。

［1］WILLIAM S.High-Performance Communication Networks［M］.Seond Edition.China Machine Press，2003

［2］张向利.基于以太网的数控系统现场总线技术研究［D］.武汉:华中科技大学，2008

［3］WANG Y L，YANG G H.H∞Controller Design For Networked Control Systems via Active-varying Sampling Period Method［J］.Acta Automatica Sinica，2008，34(7):10-13

［4］黎煊，李军，吴晓培.不确定短时延网络控制系统的故障检测［J］.控制工程，2008，15(8):78-82

［5］ANDERSON B，MOORE J.Linear optimal control［M］.Englewood Cliffs:Prentice-Hall，1971

［6］刘然，孙建忠，罗亚琴.基于环形耦合策略的多电机同步控制研究［J］.控制与决策，2010，26(6):957-960

［7］石喆，王成山.基于线性矩阵不等式理论的广域电力系统状态反馈控制器设计［J］.电网技术，2008，32(6):36-40

［8］戴洵，张文明，冯雅丽.基于非最小状态空间模型的控制器设计及仿真［J］.系统工程与电子技术，2008，18(2):19-22

［9］高一博.连续线性时变时滞系统的时滞依赖H∞控制［D］.太原:山西大学，2006

［10］OLIVEIRA M，BERNUSSOU J，GEROMEL J.A new discrete-time robust stability condition［J］.Systems ＆ Control Letters，1999，37(4):261-265