(2+1)维ZK方程的孤立波解和周期波解
康晓蓉 鲜大权
(西南科技大学理学院 四川绵阳 621010)
本文考虑如下形式的(2+1)维 Zakharov-Kuznetsov(ZK)方程:
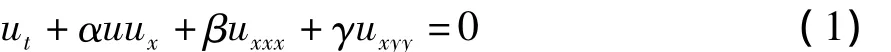
其中 α,β,γ为非零实数。1974年,Zakharov和Kuznetsov从含有冷离子和热等温电子的磁化等离子体中推导出了该模型方程。它作为与波动现象密切相关的非线性方程,既可用于描述水波在(2+1)维空间的运动规律,也可用于描述处于磁场中的等离子体的运动规律。早在20世纪90年代,Shivamoggi B.K.利用 Painleve测试法对它作了研究[1]。近年来,该方程引起了更多物理学家和数学家的关注。闫振亚等用拟设法得到了组合的(2+1)维ZK方程的钟状与扭状组合型孤波解和周期孤波解[2];Mou S.S.A.通过相似约化获得了(1)式的一些显式解[3];Abdul-Majid Wazwaz采用 sin-cos法和扩展tanh法得到了2个修正形式周期孤子解和周期解[4-5];石玉仁等用同伦分析法得到修正的方程(1)的一些近似精确解[6];闫志莲等利用改进直接法给出了广义(2+1)维ZK方程的对称和新旧显式解间的关系[7];邓朝方应用新的扩展双曲函数法,得到了方程(1)的若干周期波解[8];杨征等用改进Riccati方程映射法得到了特殊孤子解结构[9]。但方程(1)的可积性内涵丰富[10],其不同的解结构表达了不同的物理意义。
本文应用微分动力系统定性理论对方程(1)进行定性分析,并运用椭圆方程映射法寻求相应解的显式表达。
1 定性分析
取波变换:
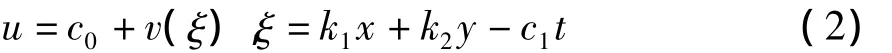
其中k1,k2,c1为待定非零常数,k1,k2分别是行波在x,y方向的波数,c1为波速,c0是式(1)的常数特解。将式(2)代入方程(1)得:
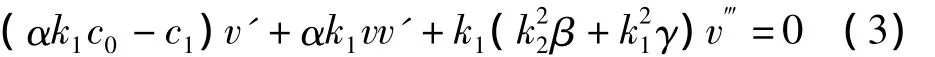
其中v'=dv/dξ,(3)式对ξ积分一次,取积分常数为A得:

记dv/dξ=w(ξ),则非线性常微分方程(4)等价于以下自治动力系统:
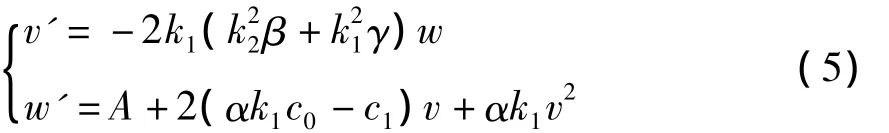
系统(5)有两个平衡点:

在平衡点处(5)式右边的Jacobi矩阵分别为:

其特征根分别为:

当(αk1c0-c1)2-αk1A>0时,λi(i=1,2)或为两不等实数,或为两共轭纯虚根。此时平衡点P1,P2或为鞍点或为中心点,且P1为鞍点时P2必为中心点,P1为中心点时P2必为鞍点。当(αk1c0-c1)2-αk1A<0时,λi(i=1,2)为两共轭复根。这时的平衡点P1,P2或为焦点或为中心点。
由(5)式可知,系统在相平面(w,v)上的相轨线满足:
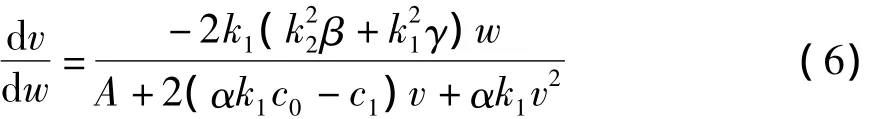
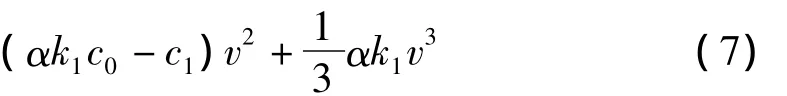
综上分析可得,系统(4)存在鞍-鞍同宿轨和围绕中心的周期闭轨。方程(1)相应地存在孤立波解和周期波解[11]。
2 孤立波解和周期波解
式(4)两边乘以v'后再对ξ积分一次,取积分常数为B得:

这是广义的常系数三次椭圆方程,下面用椭圆方程映射法和Jacobi椭圆函数展开法两个方法寻求式(8)的解。
2.1 椭圆方程映射法

依据文献[12]的相关结果得式(9)的解及式(1)的相应解。
2.1.1 孤立波解
当A=B=0,α,k1∈R- {0},(αk1c0-c1)τ>0时,(9)的解是:

ξ→ ±∞⇒v1→0,因此这是从鞍点P1=(0,0)出发又回到P1的同宿轨。相应获得(1)的孤立波解为:
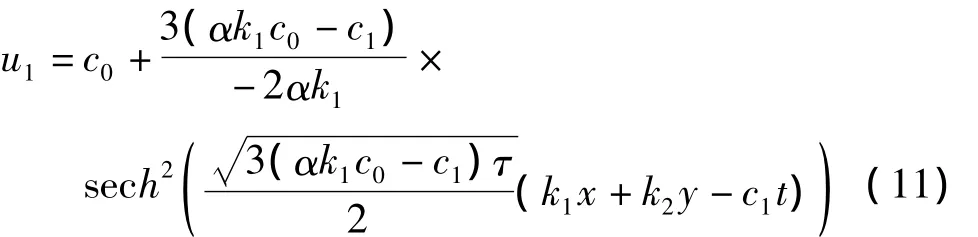
2.1.2 周期波解
(1)Weierstyass椭圆函数周期波解。
当A,B∈R,αk1τ>0,αk1c0-c1∈R时,

相应获得(1)的周期波解为:

有理函数解为:

(2)正割函数周期波解。
当A=B=0,α,k1∈R-{0},(αk1c0-c1)τ<0 时,
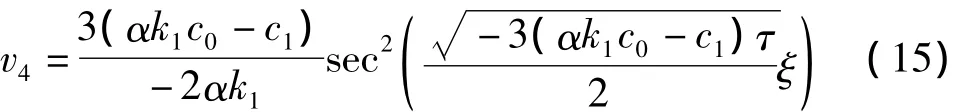
这也是围绕中心点的闭轨。式(1)的相应周期波解为:

2.2 Jacobi椭圆函数展开法

(1)假设(17)的解为:

其中sn=sn(ξ,m)是以m∈[0,1]为模的 Jacobi椭圆正弦函数,将(18)式代入(17)式得关于待定参数a0,a1,a2,A,B的非线性代数方程组如下:


这是围绕中心的闭轨。当m→1时
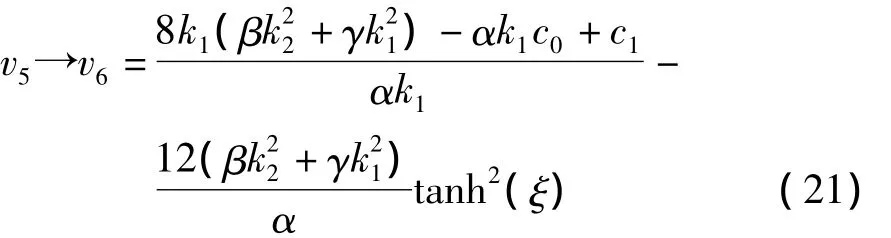
相应获得式(1)的周期波解:

孤子解:

(2)假设(17)的解为:
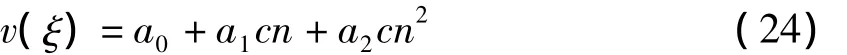
其中cn=cn(ξ,m)是以m∈[0,1]模的 Jacobi椭圆余弦函数,将(24)式代入(17)式得关于待定参数a0,a1,a2,A,B的非线性代数方程组如下(式(25)):

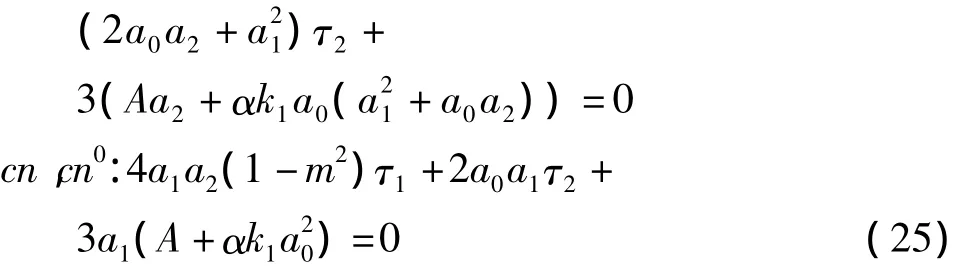
(25)的解是:

因此得式(8)的解:
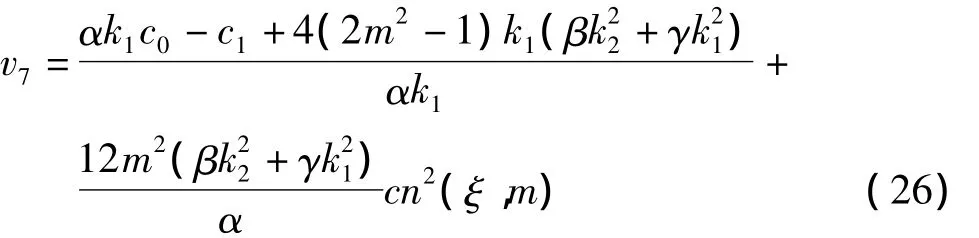
这是围绕中心的闭轨。当m→1时
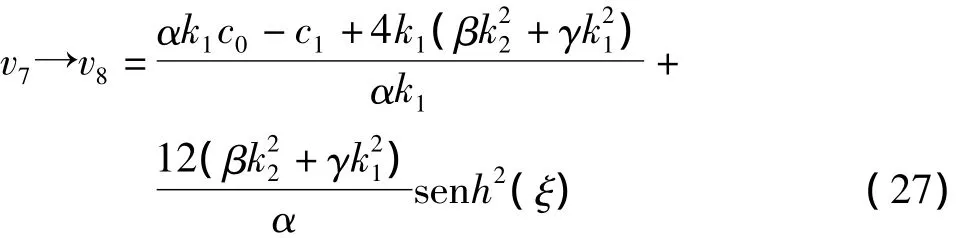
相应获得式(1)的周期波解:
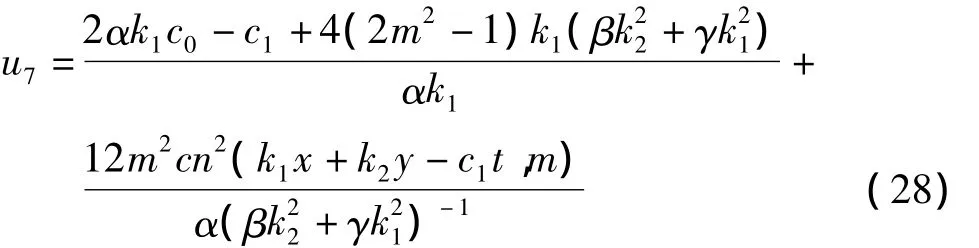
钟状孤立波解:
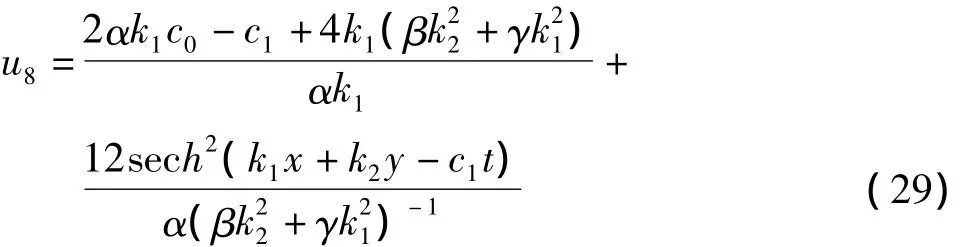
3 结论
本文应用行波变换将(2+1)维ZK方程化成了非线性常微分方程,对其进行了动力学定性分析,并运用椭圆方程映射法和Jacobi椭圆函数展开法获得了方程的孤立波解和周期波解。
[1]SHIVAMOGGI B K.Painleve test for the Zakharov -Kuznetsov equation[J].Phys,Scripta,1996,42:641-648.
[2]闫振亚,张鸿庆.组合Zakharov-Kuznetsov方程的显式孤波解[J].纯粹数学与应用数学,2000,16(2):31-35.
[3]MOUSSAM H M.Similarity solutions to nonlinear partial differential equation of physical phenomena represented by the Z - K equation[J].Int J Eng Sci,2001,39:1565-1571.
[4]WAZWAZ A M.Exact solutions with solutions and periodic structures for the Zakharov-Kuznetsov equation and itsmodified form[J]Communications in Nonlinear Science and Numerical Simulation,2005,10:597-606.
[5]WAZWAZ A M.The extended tanh method for the Z-K equation,themodified Z-K equation,and its generalized forms[J].Communications in Nonlinear Science and Numerical Simulations[In Press]dor 10.1016/j.cnsns.2006,10:007.
[6]石仁玉,许建新,等.同伦分析法在求解非线性演化方程中的应用[J].物理学报,2006,55(4):1556 -1560.
[7]闫志莲,刘希强.广义Zakharov-Kuznetsov方程的对称及精确解[J].原子与分子物理学报,2007,24(1):141-144.
[8]DENG Chao-fang.New Exact Solutions to the Zakharov-Kuznetsov and its generalized form[J].Commun Nonlinear Sci Numer Simulat,2010,15:857 -868.
[9]杨征,马松华,方建平.(2+1)维Zakharov-Kuznetsov方程的精确解和孤子结构[J].物理学报,2011,60(4):040508.
[10]肖光灿,鲜大权,肖潇.New exact solutions to the Dullin-Gottwald-Holm Equations[J].西南科技大学学报,2010,26(1):93 -99.
[11]XIANDa-quan.Saddle-node heteroclinic orbitand exact nontraveling wave solutions for(2+1)D KdV-Burgers Equation[J].Abstract and Applied Analysis,2013,696074:1-7.
[12]ZHANG S.A generalized auxiliary equation method and its application to(2+1)D KdV equations[J].Compu.and Math.with App.,2007,54:1028 -1038.

