具有离散和分布时滞的脉冲神经网络的全局指数稳定性

向泽英

(西南科技大学理学院 四川绵阳 621010)

近年来，细胞神经网络(CNNs)已经广泛应用于信号处理、图像处理、模式识别、联想记忆、信号处理和优化问题等［1－2］。细胞神经网络自提出以来，由于其广大的应用前景，对细胞神经网络系统的理论、方法和应用已经取得了不少的研究成果。如今，其研究已经发展到具有离散和分布时滞的情形［3－4］。另一方面，脉冲现象作为一种瞬时突变现象，普遍存在于现实生活中的各个科技领域，它能更好地描述某些事物的变化规律。为了扩大神经网络的适用范围，在神经网络中引入脉冲扰动是非常有必要的［5－7］。线性矩阵不等式(LMI)方法是一种处理许多控制问题的有效方法，并且它可以利用Matlab工具箱求解［8］。本文的主要目的是给出一类具有离散和分布时滞的脉冲神经网络的全局指数稳定的充分条件，基于李雅普诺夫稳定性理论和线性矩阵不等式处理方法，给出一个系统全局指数稳定性的判断方法。

1 问题描述

考虑如下的脉冲时滞神经网络模型:

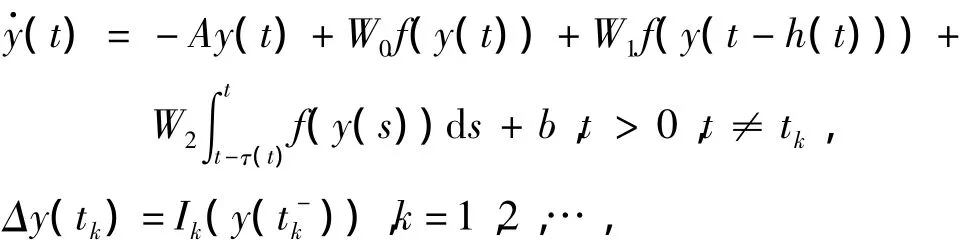
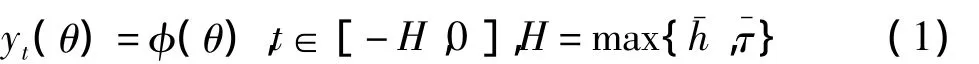
其中，y(t)=［y1(t)，…，yn(t)］T∈Rn是状态向量，f(y(t))=［f1(y1)，f2(y2)，…，fn(yn)］T是神经元激活函数，且fi(0)=0，外部输入b=［b1，…，bn］T是常向量，A=diag(a1，a2，…，an)是正定对角矩阵，表示神经元的自反馈矩阵，是神经元之间的连接权矩阵，时变时滞是h(t)有界非负函数满足0≤h(t)≤，τ(t)＞0 是时变分布时滞满足0≤τ(t)≤，并假定(t)＜hd＜1。Δy(tk)=y(tk)－y()表示在tk时刻的脉冲。

本文中假设激活函数f(y)单调不减，有界并满足Lipschitz条件，即

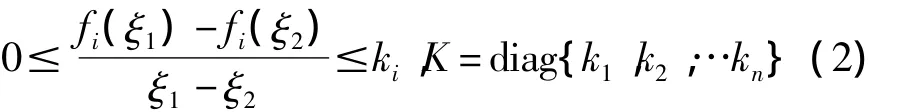
由不动点定理，系统(1)至少存在一个平衡点。将系统(1)的平衡点x*平移到原点，作变换

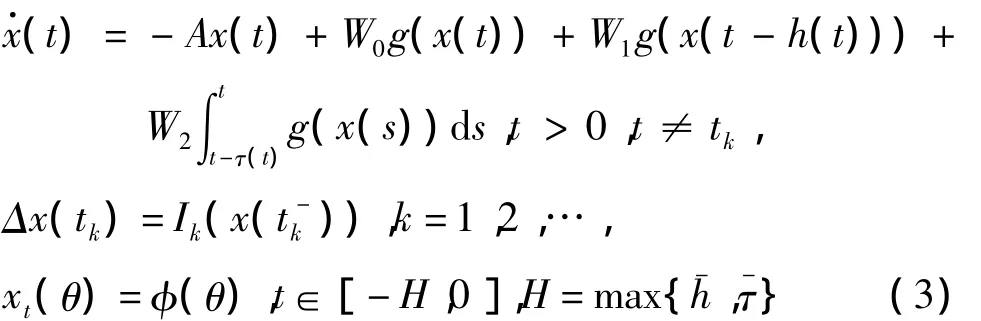
其中x(t)=［x1(t)，…，xn(t)］T∈Rn是系统(3)的状态向量，g(x)=［g1(x1)，g2(x2)，…，gn(xn)］T，，且有

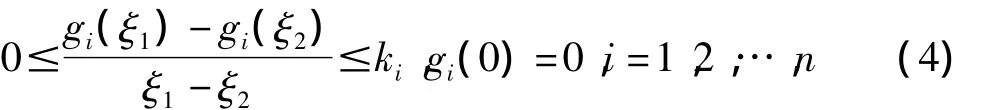
定义1 若存在常数M≥1和λ＞0，使得当t≥t0时，对所有初值都有

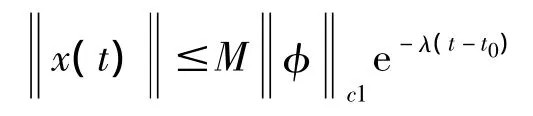
2 主要结果

成立，其中:

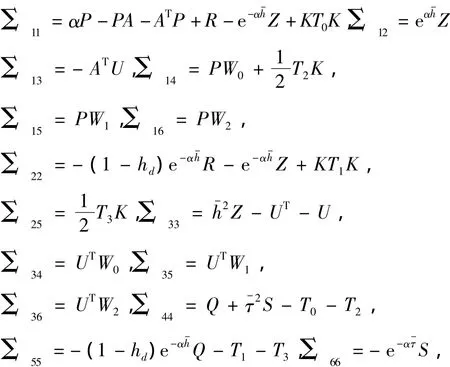
则系统(3)的零解是全局指数稳定的。

证明 考虑如下的分段Lyapunov泛函:

其中:

沿系统(3)的解轨线，计算Vi(i=1，…，5)对时间的导数:

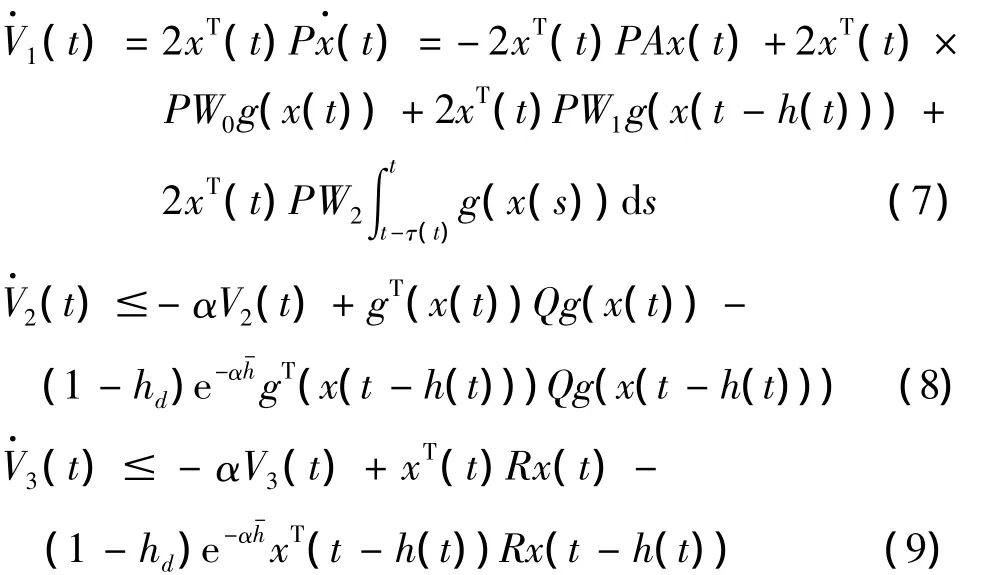
利用李普希兹条件(4)增加非负项，加“0”项等放缩手段将

放缩后可得:

其中:

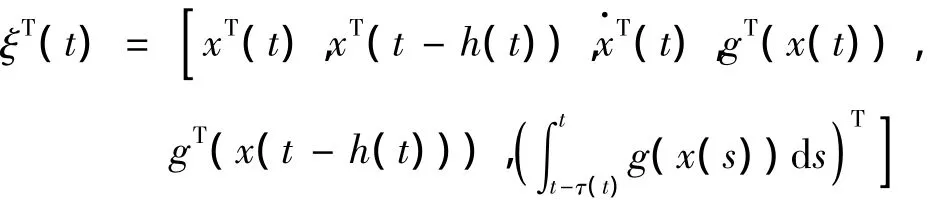
因此得:

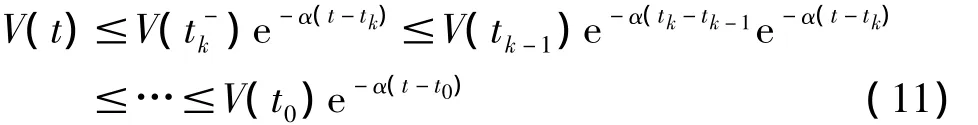
由V(t)的定义，有:

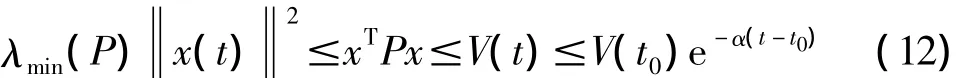
另一方面

因此有:

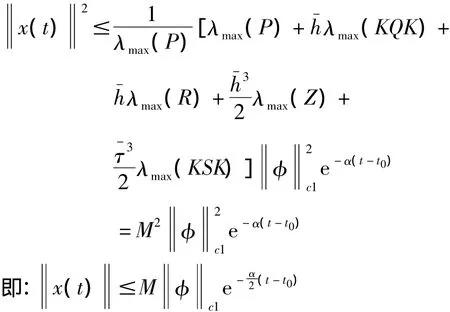
显然M＞1，因此，系统(3)的零解是全局指数稳定的，且指数收敛率为

3 结论

本文研究了一类具有离散和分布时滞的脉冲细胞神经网络的全局指数稳定性问题。通过构造分段Lyapunov泛函，利用微分方程的相关基本理论，不等式分析技巧以及线性矩阵不等式方法(LMI)得到了系统全局指数稳定的充分条件。

［1］CHUA LO，YANG L.Cellular neural networks:theory［J］.IEEE Trans Circ Syst，1988，35:1257 －1272.

［2］CHUA LO，ROSKA T.Cellular neural networks and visual computing［M］.Cambridge，UK:Cambridge University Press，2002.

［3］Kwon OM，Park JH.Delay－dependent stability for uncertain cellular neural networks with discrete and distribute time － varying delays［J］.Journal of the Franklin Institute，2008，345:766－778.

［4］BAO H B，CAO JD.Exponential stability for stochastic BAM networks with discrete and distributed delays［J］.Applied Mathematics and Computation，2012，218:6188－6199.

［5］LONG S，XU D.Delay－dependent stability analysis for impulsive neural networks with time varying delays［Z］.Neurocomputing，2007.

［6］WU B，LIU Y，LU J.New results on global exponential stability for impulsive cellular neural networks with any bounded time － varying delays［J］.Mathematical and Computer Modelling 2012，55:837 －843.

［7］ZHANG Y.Robust exponential stability of uncertain impulsive neural networks with time－varying delays and delayed impulses［J］.Neurocomputing，2011，74:3268－3276.

［8］BOYD S，GHAIUIL E，FERON E，et al.Linear Matrix Inequalities in System and Control Theory［M］.Philadelphia:SIAM，1994.