方钢管-钢骨高强度混凝土组合短柱轴心受压承载力研究
姜嘉龙,雷劲松,张 军,廖周明,廖周先
(1.西南科技大学土木工程与建筑学院 四川绵阳 621010;2.绵阳市华烨建设有限公司 四川绵阳 621000)
新型方钢管-钢骨高强度混凝土组合短柱巧妙 结合了钢骨混凝土柱和钢管混凝土柱二者的优点,它是在方钢管中插入工字型或者十字形的型钢后填充混凝土而形成的。与传统钢-混凝土组合柱相比,具有极限承载力与延性高、空间利用率高、耐火性优异、易于施工、经济效益出众等特点[1]。近年来,国内外学者从不同角度对钢管混凝土结构进行了大量试验与理论研究,提出了不少的承载力理论计算公式,从本质上看,对于钢管混凝土结构理论研究方法的区别在于怎样考虑存在于外包钢管与核心混凝土之间相互作用的紧箍力,而这些理论公式主要是基于钢管混凝土统一理论、拟钢或拟混凝土理论或者叠加理论推导的。本文在前人研究的基础上,根据极限平衡理论推导钢管混凝土结构的分析思路,在方钢管-钢骨高强度混凝土组合短柱中各组成部分变形方式与极限条件已知的情况下,对方钢管-钢骨高强度混凝土组合短柱轴压极限承载力计算公式进行推导验证。
1 组合短柱轴压受力模型及基本假设
在轴压初期,可以认为新型组合截面的承载力是由钢管、核心高强度混凝土和钢骨三部分叠加承担的,因为钢管相较于混凝土而言具有更大的泊松比,所以,方钢管-钢骨高强度混凝土组合短柱承受的轴压荷载按照钢管和混凝土的刚度比分配,且呈现出互相脱离的趋势。荷载持续增大,开始进入弹塑性阶段,这时,混凝土的泊松比也随之增大且超过钢管,由此带来的是混凝土的横向应变超过钢管的横向应变,产生相互作用力即我们所说的套箍作用。然而由于弹塑性阶段组合柱的受力及变形过程复杂,所以本文采用极限平衡法,也称极限分析方法,直接根据组合短柱在极限状态时的平衡条件计算出其截面的极限承载力,该方法直接跳过了复杂的弹塑性阶段,不需给出材料的本构关系,因此极限承载力的计算得到大大简化。本文参考文献[2]-[4],基于极限平衡理论推导在较小长细比条件下的方钢管-钢骨高强度混凝土组合短柱的极限承载力公式。计算模型的基本假设如下:
(1)在组合柱失稳之前,组合柱以及各个部分的形变很小,因此,忽略极限平衡方程中的几何形状的变形。
(2)将钢管、混凝土和钢骨看成是组成组合柱结构的三个单元,极限状态下,忽略钢骨周围区域应力的不均匀性,把整个组合柱截面看做均匀受力,同时忽略钢管壁的径向应力且认为径向和环向应力都是均布的,受力示意图如图1所示。
(3)引入钢管等效约束折减系数ξ[5]以及考虑尺寸效应影响的混凝土强度折减系数γu[6],用来将方钢管对混凝土的约束以及混凝土强度等效替换成相应的圆钢管对混凝土的约束以及混凝土强度。等效示意图如图2所示。
(4)组合短柱钢管服从Von Mises屈服条件;钢骨不考虑混凝土对其的约束作用,因此处于单向受压应力状态,且屈服条件为σs=fys;高强度混凝土的屈服条件分为线性和非线性两种[3,7],本文采用线性条件进行分析,即σc=fc(1+kp/fc)。

图1 钢管、核心混凝土受力示意图Fig.1 The stress diagram of steel tube and core concrete

图2 方钢管等效为圆钢管示意图Fig.2 The diagram of square steel tube equivalent to circular steel tube
2 极限承载力公式推导
由受力示意图图1可知,在极限状态下,由静力平衡可得:

其中:r,t0-钢管的内径及其管壁厚度;σxt,pr-钢管环向应力及核心混凝土所受紧箍力;At,Ac,As-钢管、核心混凝土及型钢截面面积;σyt,σc,σys- 考虑了各元件相互作用的钢管、核心混凝土以及型钢的纵向压应力。
由极限屈服条件可得:
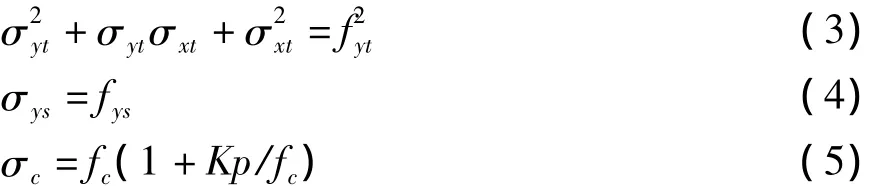
其中:fys-型钢屈服强度;fc-混凝土轴心抗压强度;K- 测压系数,其取值范围为 3,4,5,6,一般情况下取K=4[3],在本文中,将取3和4进行分析。
2.1 方钢管承载力表达式
根据文献[7],将方钢管-钢骨混凝土组合短柱的方钢管截面积、核心混凝土与钢骨截面积之和以等面积的方法等效为圆钢管-钢骨混凝土组合短柱的圆钢管、核心混凝土与钢骨截面积之和,其转化公式为:

其中:B,t-方钢管的外边长、管壁厚度。
由于方钢管对其核心混凝土的约束力大小不及圆钢管对其核心混凝土的约束力,且约束力不像圆钢管中约束力那样均匀分布,因此,在将方钢管-钢骨混凝土组合短柱向圆钢管-钢骨混凝土组合柱等效代换时,引入考虑钢管厚边比υ(υ=t/B)的等效约束折减系数ξ[5],其意义为受约束方钢的一条边上的计算比例长度。ξ的计算公式如下:
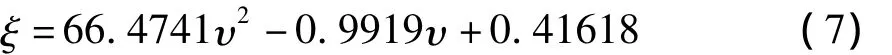
由此可知,方钢管对其核心混凝土的紧箍力为:

其中:pr-等效圆钢管内核心混凝土受到的紧箍力。
由式(1),(3)及(8)可得:
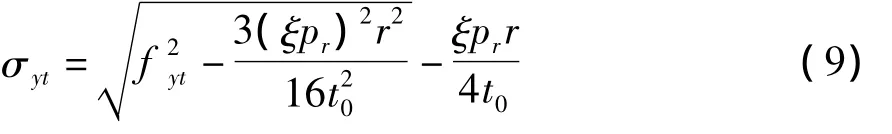
因为钢管外径R=r+2t0,且r≫t0,可近似求得:

将式(10)代入式(9)得

设套箍系数θ=Atfyt/Acfc,将其代入式(11)并整理得:

因此,方钢管承载力表达式为:

2.2 核心混凝土承载力表达式
由于在方钢管-钢骨高强度混凝土组合短柱中方钢管对核心混凝土的约束分为有效约束区和非有效约束区,所以在将方钢管等效为圆钢管时,为了考虑前述非约束区域对核心混凝土约束减弱的影响,本文引入混凝土强度折减系数[6]γu=1.67r-0.112,即方钢管内核心混凝土承载力表达式为:

将式(5)及(8)代入上式可得:
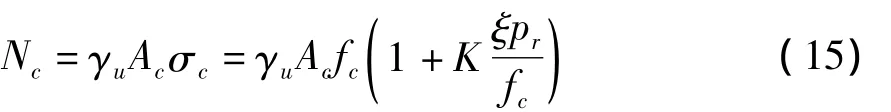
2.3 钢骨承载力表达式
由于不考虑混凝土对钢骨的约束作用,使得钢骨处于单向受压应力状态,且屈服条件为σs=fys,因此可得钢骨的承载力表达式为:

2.4 组合短柱承载力表达式
按极限平衡理论的叠加原则,钢管-钢骨高强度混凝土组合短柱的极限承载力由它的组成部分各自的承载能力决定,即有:

代入公式(13),(15)及(16)可得:

从上式可以看出,组合短柱轴压承载力N0是钢管内核心混凝土受到的紧箍力pr的函数,为求组合短柱轴压极限承载力Nmax0,将式(18)对pr求导,且由极值条件有:

代入式(18)可得:

求解式(20)可得对应Nmax0时的钢管内核心混凝土受到的紧箍力值为:
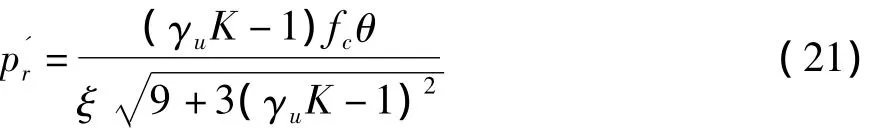
将上式代入式(18)可得:

3 公式计算结果验证分析
在本文中,方钢管-钢骨高强度混凝土组合短柱轴压极限承载力表达式(22)中的K系测压系数,取3和4进行分析。同时,本文选取文献[8]中推荐的钢骨-钢管高性能混凝土组合短柱轴压极限承载力计算公式进行计算,其极限承载力计算公式分别为:

其中:θ,η分别为套箍系数和配骨系数,θ=Atfyt/Acfc,η=Asfys/Acfc;α为考虑钢管对核心混凝土约束作用的系数,在常用含钢量范围内近似取值为 1.2。
如下文所示,表1、表2分别列出了文献[9]中的轴压极限承载力试验结果与本文及文献[8]所推导的组合短柱轴压极限承载力公式(22),(23)计算结果及比较分析。

表1 各公式计算结果Table 1 calculated results by Different formulas

表2 承载力公式分析Table 2 Analysis of bearing capacity formulas
表1、表2的计算结果显示,本文基于极限平衡原理推导的极限承载力公式(22)的计算结果随着K值的变化而变化,当K=4时,极限承载力计算值较试验值偏大,安全性降低,当K=3时,计算值与试验值吻合良好;与此同时,由公式(23)计算的结果与试验值吻合程度也令人满意。
通过进一步比较,文献试验值与本文推导的K值取3时的式(22),式(23)计算的组合短柱极限承载力的比值的平均值分别为1.021及1.047,验证了本文推导的方钢管-钢骨高强度混凝土组合短柱轴压极限承载力公式(22)在K=3时的合理性以及其良好的吻合度。
4 结论
本文结合有关文献中的理论及试验研究,推导了新型方钢管-钢骨高强度混凝土组合短柱在轴心受压条件下的承载力理论计算公式,初步得到以下结论:基于极限平衡理论,跳过弹塑性阶段组合柱的受力及变形过程复杂,直接根据组合短柱在极限状态时的平衡条件推导出方钢管-钢骨高强度混凝土组合短柱轴压极限承载力计算公式;通过文献中的试验分析数据,验算比较了本文及其他学者推导的方钢管-钢骨高强度混凝土组合短柱轴压极限承载力计算公式,结果显示,本文基于极限平衡理论推导的组合短柱轴压极限承载力计算结果具有更好的吻合度,同时具有较为适当的安全储备,对实际工程的初步设计提供了一定的理论依据。
[1]钟善桐.钢管混凝土统一理论——研究与应用[M].北京:清华大学出版社,2006.
[2]肖阿林.钢骨-钢管高性能混凝土轴压组合柱受力性能与设计方法研究[D].湖南:湖南大学博士学位论文,2009.
[3]蔡绍怀.现代钢管混凝土结构(修订版)[M].北京:人民交通出版社,2007.
[4]何益斌,张铁成,肖阿林,等.极限平衡法分析钢骨-钢管混凝土短柱极限承载力的简化方法[J].铁道科学与工程学报,2006,5(3):46 -49.
[5]李小伟,赵均海,朱铁栋,等.方钢管混凝土轴压短柱的力学性能[J].中国公路学报,2006,19(4):77 -81.
[6]KENJIS,HIROYUKIN,SHOSUKE M,et al.Behavior of centrally loaded concrete filled steel tube short columns[J].Journal of Structural Engineering,2004,13(2):180-188.
[7]丁发兴,余志武.钢管混凝土短柱力学性能研究——实用计算方法[J].工程力学,2005,33(5):134-138.
[8]朱美春.钢骨-方钢管自密实高强度混凝土柱力学性能研究[D].辽宁:大连理工大学博士学位论文,2005.
[9]朱美春,王清湘,冯秀峰.轴心受压钢骨-方钢管自密实高强度混凝土短柱的力学性能研究[J].土木工程学报,2006,39(6):35-41.

