中小学生对比例推理的过度使用

李晓东，江荣焕，钱玉娟



中小学生对比例推理的过度使用

李晓东，江荣焕，钱玉娟

（深圳大学 师范学院，广东 深圳 518060）

以370名5~8年级的中小学生为研究对象，考察学生在以缺值形式呈现的比例问题和加法问题上的表现．结果表明，年级与问题类型存在显著的交互作用，除5年级外，其它年级的学生在比例问题上的成绩均优于加法问题．学生在加法问题上存在过度使用比例推理的现象，并且在小学6年级时达到高峰．数字比与小学生过度使用比例推理有关，当同类量比与不同类量比均为整数时，学生更容易在加法问题上犯比例错误．

比例推理；缺值问题；数字比

1 问题提出

比例推理是关于数量关系的思考，要求同时对几个数量或值做出比较．关于比例推理，人们很容易联想到比与比例问题，实际上比例推理的应用非常广泛，不仅是数学领域，其它学科如科学与艺术也需要运用比例推理的知识．日常生活更是离不开比例推理，如选择哪一款电器性价比更高或是选择哪种电信套餐更划算，等等．比例推理虽然重要，但是国外有研究表明中小学生存在过度使用比例推理的现象．例如，Verschaffel等人发现，对于“Ellen和Kim在同一个跑道上跑步，他们跑步的速度相同，但是Ellen比Kim后起跑，当Ellen跑了5圈时，Kim跑了15圈．当Ellen跑到30圈的时候，Kim跑了多少圈？”这种本应使用加法解决的问题，大多数6年级学生错误地给出比例答案“30×3=90”，而不是加法答案30+10=40[1]．对于“Jim的100米短跑的最好成绩是17秒，问Jim跑1000米需要多长时间？”这种根本没有确切答案的问题，超过90%的10~12岁学生会回答170秒[1]．

为什么学生在本该使用加法思维的问题上使用了乘法思维（比例推理）？一种看法是教科书上的比例问题常以缺值形式呈现，即在问题中，依次给出、、三个数，要求求出第四个数，使得/=/，或/=/．在缺值形式的问题中，与、与之间或与、与之间有相同的线性关系，它们之间的比相等．例如，在“2件衬衣卖30元，4件相同的衬衣卖多少钱？”这个问题中，2/4与30/？具有相同的比，而2/30与4/？也具有相同的比，因此利用已知比就可以求出未知数．学生在长期的练习中，错误地将问题的表面结构当成问题解决的线索，而没有对数量之间的真正关系建立表征．

还有研究表明，题目中数字之间的整数比会诱导个体在测试中使用比例方法[2]，例如在上面Ellen和Kim跑步这个题目中，由于15/5=3，因此个体更容易以30×3=90来计算Kim跑的圈数．Karplus等人的研究表明，对于“一种柠檬水由杯柠檬汁兑杯水混合而成，现在有杯柠檬汁，若要调出味道相同的柠檬水需要多少杯水？”这样的题目，如果/或者/为整数的话，被试更容易运用比例策略解决问题从而获得正确答案，而当这些比不为整数时，被试更容易运用加法策略来解决问题，如采用等式=c+(-)解题，从而导致错误的答案．可见，题目中的数字比与被试使用的问题解决策略有关系[3]．Linchevski等人的研究则发现当(5)已知时，学生会倾向于认为(20)=4×(5)，他们指出“也许我们对数字的选择诱发了被试对比例的错误应用……如果不使用20，而是使用17、27或83等数字，学生们就不会错误地使用比例方法了”[4]．Van Dooren等人在2009年的研究进一步证实，题目中的数字比会影响学生对比例推理的误用，他们发现，如果题目中的数字比为整数，那么学生运用比例策略解题的倾向会增加，从而导致其在非比例题上的成绩更差，而当题目中的数字比为非整数时，学生较少运用比例策略解题，从而减少了比例推理的误用[5]．

国内关于比例推理的研究较少，苗丹民于1991年以中国4~14岁儿童为研究对象，率先探讨了儿童比例推理能力的发展，研究表明儿童比例推理能力的发展随着年龄的增长呈现出阶段性，儿童比例推理能力在4~6岁时处于加法推理阶段，仅能认识到多与少的关系，之后逐渐过渡到乘法推理，开始理解整数倍数的概念，最后约在12岁时达到函数关系的推理水平，能够对非整数倍函数关系进行操作和整合[6]．近几年的研究则更多探讨了儿童比例推理策略的发展及其影响因素，陈英和等人的研究表明，随着年级增长，儿童的比例推理策略从加法策略向倍数乘法策略转化，在6年级时出现比例公式策略，其中题目中的整数和分数会影响学生比例策略的使用，当整数出现时，儿童更容易采用比例策略，并且在加入解释题目的图例之后，儿童能够更好地运用正确的策略进行解题，更少出现逻辑错误[7]．可见，儿童比例推理的正确使用不仅受题目中数字的影响，还有赖于他们对题目的正确理解．

有关中国儿童与国外儿童的跨文化研究表明中西方学生的数学能力具有明显的差异．苗丹民的研究对比了中加儿童的比例推理能力，发现11~14岁的中国儿童比例推理能力的发展比同龄加拿大儿童要快．也有研究表明，中国儿童在数学运算领域的能力比国外的儿童要强，在几何空间推理能力方面国内外儿童则没有明显的差异[8]．綦春霞等人采用PISA（国际学生评估项目）对中英学生的数学推理能力进行比较，发现对于两国的8年级学生，英国学生在代数推理和概率推理方面得分更高，而中国学生则在几何推理方面得分更高[9]．夏小刚等人对中美学生数学思维的差异进行比较，发现在问题解决过程中，中国学生偏向于使用抽象的策略和符号表征，而美国学生往往更偏向使用视觉策略和具体表征[10]．

从目前公开发表的文章来看，尚未看到中国学生是否存在过度使用比例推理现象的研究．那么，国外学生普遍存在的过度使用比例推理的现象在中国中小学生中是否也存在呢？数字比的形式即两个数量的比是否为整数是否与过度使用比例推理有关呢？这里拟参考Van Dooren等人的研究架构对上述问题进行探讨．

2 研究方法

2.1 被 试

被试为南方某普通小学和某普通中学的学生，共370人（男193人，女177人）．其中5年级学生72人（男28人，女44人），平均年龄为10.30岁；6年级学生76人（男40人，女36人），平均年龄为11.26岁；7年级学生110人（男62人，女48人），平均年龄为12.24岁；8年级学生112人（男63人，女49人），平均年龄为13.49岁．所有被试智力正常，以前未参加过类似实验．

公安院校思想政治理论课的建设是一项意义深远又极富挑战的工程，思政课教师既拥有广阔发展空间，也承载着伟大时代使命。要始终铭记：不忘初心，牢记使命，用好课堂教学的主渠道，切实将思政课打造成学生一见钟情、念念不忘、真心喜爱、终身受益的课程。

2.2 实验材料

研究中的问题有两种，一是比例问题，一是加法问题，均以缺值形式呈现．数量之间的比称为数字比，分为同类量比和不同类量比．如在“2件衬衣卖30元，4件相同的衬衣卖多少钱？”这个问题中，2代表衣服的数量，30代表衣服的价格，它们之间的比就是不同类量比；而2与4都表示衣服的数量，它们之间的比称为同类量比．

数字比有4种组合类型：（1）同类量比和不同类量比均为整数；（2）同类量比为整数，不同类量比为非整数；（3）同类量比为非整数，不同类量比为整数；（4）同类量比和不同类量比都为非整数．

比例问题与加法问题各8道，每种数字比类型的题目各2道．数字比最小为2，最大为4．所有题目的最终正确答案均为整数．各种类型试题样例见表1．

表1 4种数字比类型的题目样例

注：A代表同类量比与不同类量比均为整数；B代表同类量比为整数，不同类量比为非整数；C代表同类量比为非整数，不同类量比为整数；D代表同类量比与非同类量比均为非整数．

2.3 实验程序

由受过培训的心理学专业研究生担任主试，在教室里进行团体施测．

为控制顺序误差，采用系统ABBA法进行平衡，A为比例问题，B为加法问题，而对每一种问题类型下具有不同数字比的题目进行拉丁方平衡．最终得到两种顺序，实验中同桌被试接受不同的测验顺序．在实验开始前，为了避免学生产生紧张情绪，告知被试主试是研究生正在做毕业论文，需要做一个关于学生学习情况的一个小调查，不是考试不计成绩，请不用紧张．实验过程中，要求被试独立完成，只需列算式和写答案，不需要写下演算步骤，从开始到结束，实验持续时间为25分钟左右．所有数据均采用SPSS16.0统计软件包进行处理与分析．

3 结果与分析

做对1题得1分，比例问题与加法问题的分值范围皆为0~8分．若只列算式，没有写答案，只要列式正确，则认为是正确的；如果只写答案，但未列算式，只要答案是最终的正确答案，也算正确．

3.1 中小学生在比例问题与加法问题上的成绩

5~8年级学生解决比例问题及加法问题成绩的平均数和标准差见表2．

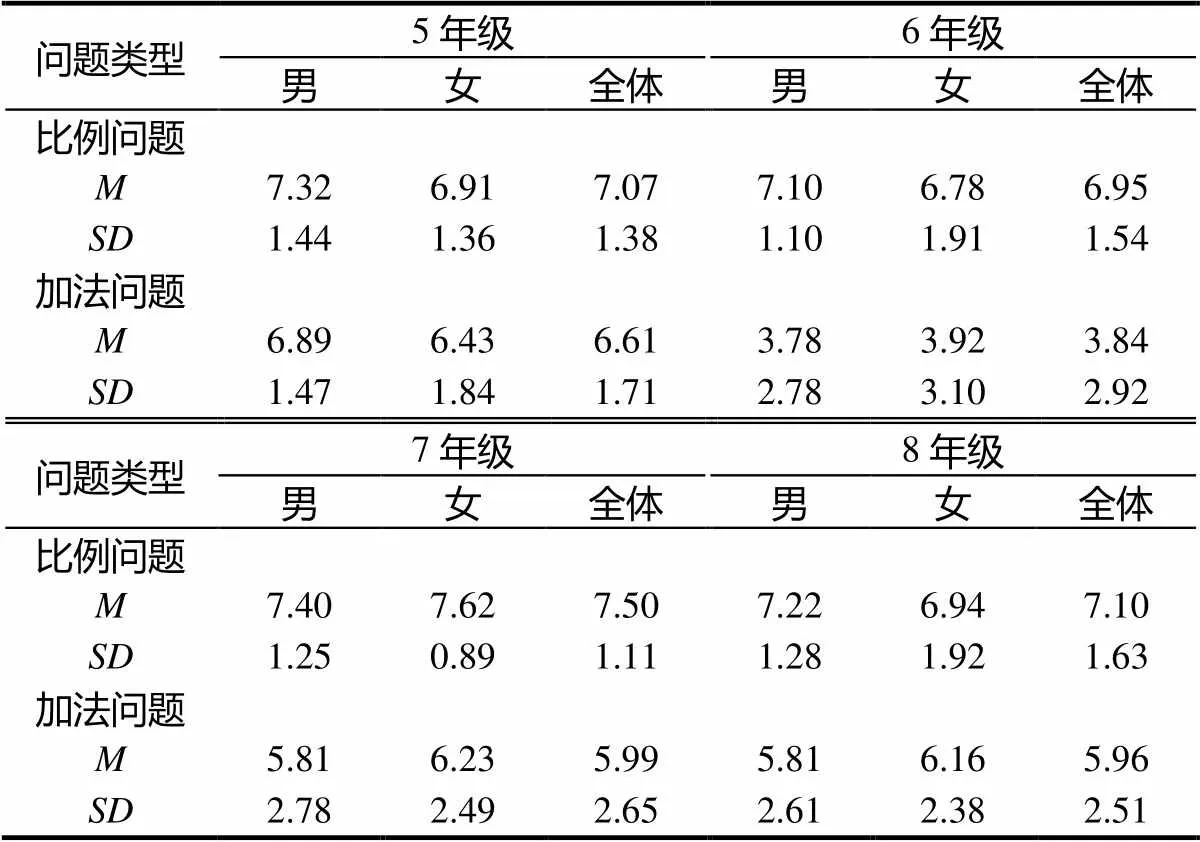
表2 5~8年级学生解决比例问题及加法问题成绩的平均数和标准差

以年级、性别、问题类型作为自变量，各类题目上的成绩为因变量，进行4(年级)×2(性别)×2(问题类型)的重复测量的方差分析．结果表明，问题类型的主效应显著，(1, 362)=98.165，<0.001；年级主效应显著，(1, 362)=17.283，<0.001；性别主效应不显著，(1, 362)=0.074，=0.786；问题类型与年级的交互作用显著（见图1），(3, 362)=11.44，<0.001；问题类型与性别的交互作用不显著，(1, 362)=1.024，=0.312；年级与性别的交互作用不显著，(3, 362)=0.989，=0.398；3者之间也不存在交互作用，(3, 362)=0.234，=0.873．

由于问题类型与年级的交互作用显著，因此作简单主效应分析．首先检验年级一定时，问题类型的简单主效应．配对样本检验的结果表明，除5年级外，其它3个年级在比例问题和加法问题上的成绩差异均显著，被试在比例问题上的成绩均优于加法问题（5年级：(71)=1.767，=0.081；6年级：(75)=8.588，<0.001；7年级：(109)=5.318，<0.001；8年级：(111)=4.053，<0.001）．

其次，考查问题类型一定时，年级的主效应．结果表明,在比例问题上，存在显著的年级差异，(3, 366)=2.798，<0.05．事后比较发现，7年级在比例问题上的成绩显著好于5、6、8年级（7-5=0.431，<0.05；7-6=0.553，<0.05；7-8=0.402，<0.05），而5、6、8年级在比例问题上的成绩无显著差异；在加法问题上，存在显著的年级差异，(3, 366)=17.888，p <0.001．事后比较发现，6年级成绩显著低于5、7、8年级（5-6=2.796，<0.001；7-6=2.149，<0.001；8-6=2.122，<0.001），而5、7、8年级在加法问题上的成绩无显著差异．此外，研究中发现性别对成绩的影响既无主效应又与其它变量无交互作用，因此在后面的分析中均不考虑性别因素的影响．

3.2 中小学生在比例问题与加法问题上的错误类型

从中小学生在比例问题与加法问题的成绩看，学生在比例问题的成绩是显著好于加法问题的．按学生掌握数学知识的顺序来讲，学生是先获得加法思维，然后才学习乘法思维的，其在加法问题上的成绩应该好于比例问题．学生在缺值形式的加法问题上成绩较差是否是因为比例推理的过度使用呢？即在加法问题上使用了比例方法？学生的错误与数字比是否有关系？

图1 年级与问题类型的交互作用

经过分析，发现学生在比例问题的错误可分为两种，一是加法错误，本该用比例方法解决的却运用了加法；另一类是没有规律的错误，干脆不会未给出答案的也归为此类，称为其它错误．学生在比例题上所犯错误的类型及其占答案总数的百分比见表3．

以年级为层变量，采用2(错误类别)×4(数字比)的卡方检验对各年级学生在比例题上所犯的错误进行分析，结果表明各年级的学生所犯错误的类型与数字比均无关（5年级：2(3)=0.555，=0.908；6年级：2(3)=2.056，=0.561；7年级：2(3)=3.560，=0.313；8年级：2(3)=1.323，=0.724），说明各年级学生在比例题上的错误不受数字比的类型的影响．各年级在比例题上的错误占答案总数的百分比均较低，除了6年级之外，其他年级犯两类错误占答案总数的百分比均少于10%．

表3 各年级学生在比例问题上所犯的错误个数（%）

注：A代表同类量比与不同类量比均为整数；B代表同类量比为整数，不同类量比为非整数；C代表同类量比为非整数，不同类量比为整数；D代表同类量比与非同类量比均为非整数．

学生在加法问题上的错误也可分为两种，一是比例错误，即应该用加法却错误地运用了比例方法，属于比例推理的过度使用；另一类是没有规律的错误及未给出答案，称为其他错误．学生在加法问题上所犯错误的类型及其占答案总数的百分比见表4．

表4 各年级学生在加法问题上所犯的错误个数（%）

注：A代表同类量比与不同类量比均为整数；B代表同类量比为整数，不同类量比为非整数；C代表同类量比为非整数，不同类量比为整数；D代表同类量比与非同类量比均为非整数．

以年级为层变量，采用2(错误类别)×4(数字比)的卡方检验对学生在加法问题上所犯错误进行分析，结果表明5年级的错误类别与数字比有关，2(3)=12.763，＜0.01，学生在加法问题上出现的比例错误（68个，占全部错误的68%）明显多于其他错误，其比例错误按照A，D，C，B依次递减，当数字比类型为A即数字比均为整数时，出现的比例错误最多（31个）；6年级的错误类别与数字比有关，2(3)=10.476，＜0.01，学生在加法问题上出现的比例错误（261个，占全部错误的82.59%）明显多于其他错误，而其比例错误按A，C，B，D的顺序依次递减，当数字比类型为A时，错误个数最多（84个）；7年级的错误类别与数字比无关，2(3)=6.408，=0.09，但学生在加法问题上出现的比例错误（187个，占全部错误的84.62%）明显多于其他错误；8年级的错误类别与数字比无关，2(3)=4.633，=2.01，但学生在非比例问题上出现的比例错误（185个，占全部错误的81.14%）明显多于其它错误．

综上，各个年级均表现出在加法问题上犯比例错误的倾向，且5年级和6年级的学生过度使用比例推理的倾向受数字比的影响，当数字比为整数时过度使用比例推理的现象更为明显．

4 讨 论

比较了中小学生在以缺形式呈现的比例问题和加法问题上的表现，结果发现5~8年级的学生在比例问题上成绩较好，在满分为8分的题目中，各年级平均得分均达到7分以上，说明中小学生很好地掌握了比例问题的解决方法，具备了利用乘法思维解决问题的能力．但是，在本来应更为简单的加法问题上，中小学生的表现却不尽人意，成绩均低于比例问题．为什么会出现这种成绩逆转的情况呢？可能是由问题的呈现形式造成的．数学是一种基于相似性的探索活动[12]．学生在学习解决比例问题时，问题往往以缺值形式呈现，已知3个数量，求第四个量，数量之间存在比例关系．学生在学习这类问题时，将问题的呈现形式作为一种提示题型的线索储存在大脑中，遇到同类问题时就会激活比例问题的解决策略，因而会促进比例问题的解决．但是，但学生遇到表面相似而实则不同的加法问题时，激活的比例问题策略反而会导致错误的解答．

从学生在加法问题上所犯的错误来看，支持上述分析．各年级学生所犯的比例错误显著多于其它错误，尤其是6年级的错误最多．如何解释这种年级差异呢？可能与学生所受的数学教育有关．在我国，比与比例的知识要到6年级才学习，也就是说6年级的学生正式接受用比例推理解决问题的数学训练．用比例方法解决问题对6年级学生来说是一种新知识，他们对其掌握得还不够深入与扎实，对比例推理的适用范围与边界缺少清晰的认识，易受题型的误导．而7、8年级的中学生在认知和元认知能力上都优于小学生，他们已具备较高水平的比例推理能力以及对不同问题进行分析和诊断的能力，因而成绩较为理想．5年级学生在比例问题的成绩上反而好于6年级学生，可能是由于我国学生在学习乘除法时，老师会强调运用单位量的方法解决问题，因此，他们虽然没学习比与比例的问题，但他们利用单位量的方法同样可以正确解决比例问题；而在加法问题上，因为没有比与比例问题的经验干扰，反而可以用以往的加法思维正确解决问题．

研究发现数字比对学生过度使用比例推理的影响仅限于5、6年级，当同类量比与非同类量比均为整数时，小学生更倾向于在加法问题上使用比例方法，这个结果与Van Dooren等人的结果一致[5]，他们发现，对于小学4、5、6年级的学生来说，非整数比会降低学生在加法问题上使用比例方法的错误．研究发现虽然整数比增加了比例方法的应用，但非整数比却没有增加加法方法的应用，在比例问题上，各年级所犯的错误与数字比无关，这一点与国外的研究不一致[11]，这可能与两个研究使用的题目不一样有关，也可能是由于不同国家学生数学能力或教学差异造成的，未来还需要进一步探讨．

5 结 论

中国中小学生在解决比例问题时有较好的表现，但在解决以缺值形式呈现的加法问题存在过度使用比例推理的现象，6年级学生最为明显．对于5、6年级的小学生来说，整数比会增加学生在加法问题上的比例错误．

[1] Verschaffel L, De Corte E, Lasure S. Realistic Considerations in Mathematical Modeling of School Arithmetic Word Problems [J]., 1994, (4): 273–294.

[2] De Bock D, Van Dooren W, Verschaffel L. Students’ Overuse of Linearity: An Exploration in Physics [J]., 2011, 41(3): 389-412.

[3] Karplus R, Pulos S, Stage E.[M]. New York: Academic Press, 1983.

[4] Linchevski L, Olivier A, Sasman M, et al. Moments of Conflict and Moments of Conviction in Generalizing [A]. In: Olivier A, Newstead K.[C]. South Africa: International Group for the Psychology of Mathematics Education, 1983.

[5] Van Dooren W, De Bock D, Evers M, et al. Students’ Overuse of Proportionality on Missing-Value Problems: How Numbers May Change Solutions [J]., 2009, (3): 187-211.

[6] 苗丹民．4—14岁儿童比例推理及认知结构的发展研究[J]．心理学报，1991，（2）：167-177．

[7] 陈英和，赖颖慧，尹称心．数学学科领域内儿童比例推理策略的发展特点及影响因素[A]．见：中国心理学会.第十五届全国心理学学术会议论文摘要集[C]．中国心理学会，2012．

[8] 吴汉荣，李丽，约翰·哈夫勒．中德学龄儿童数学能力发展水平跨文化研究[J]．中国临床心理学杂志，2006，（3）：321-323．

[9] 綦春霞，王瑞霖．中英学生数学推理能力的差异分析——八年级学生的比较研究[J]．上海教育科研，2012，（6）：93-96．

[10] 夏小刚，吕传汉．跨文化视野下中美学生数学思维差异的比较[J]．比较教育研究，2006，（8）：63-67．

[11] Fernández C, Llinares S, Van Dooren W, et al. The Development of Students’ Use of Additive and Proportional Methods Along Primary and Secondary School [J]., 2012, 27(3): 421-438.

[12] 宁连华．数学推理的本质和功能及其能力培养[J]．数学教育学报，2003，12（3）：42-45．

5~8 Graders’ Overuse of Proportionality on Missing-Value Problems

LI Xiao-dong, JIANG Rong-huan, QIAN Yu-juan

(Normal College, Shenzhen University, Guangdong Shenzhen 518060, China)

This study examined the performance of 5~8 graders on proportional and additive missing-value problems. Results showed that there was a significant interaction between grade and problem type. Students performed better on proportional problems than additive problem except 5 graders. Students especially 6 graders turned to overuse of proportionality on additive problems. Primary school students’ overuse of proportionality was related to ratios between numbers in the problems. When both the external ratio and the internal ratio are integer, they used more proportional methods on additive problems.

proportional reasoning; miss-value word problem; ratios between numbers

2014–08–06

深圳市教育规划“十二五”重点课题——学习质量的评估与促进

李晓东（1965—），女，辽宁沈阳人，教授，博士生导师，主要从事学习与认知、数学问题解决等研究．

G420

A

1004–9894（2014）06–0073–05

[责任编校：周学智]