初中数学实验的理论研究与实践探索

董林伟，孙朝仁



初中数学实验的理论研究与实践探索

董林伟1，孙朝仁2

（1．江苏省中小学教学研究室，江苏 南京 210013；2．江苏省连云港市教育科学研究所，江苏 连云港 222006）

数学实验是通过动手动脑“做”数学的一种数学学习活动，是学生运用有关工具（如纸张、剪刀、模型、测量工具、作图工具以及计算机等），在数学思维活动的参与下进行的一种以人人参与的实际操作为特征的数学验证或探究活动．国外研究较早，进入21世纪后，中国中学开始探索、实施数学实验．以江苏省教育科学规划课题为依托，历时五年多，对初中数学实验进行了系统的研究与实践，内容涉及数学实验的价值及目标、概念界定、可行性调查、基本类型、设计原则及其元素、实施模式及评价等．

数学实验；理论研究；实践探索

1 研究背景

在中国传统教育观念中，数学一直被认为仅仅是训练人脑理性思维、抽象逻辑思维的学科，因而在中学数学教育中形象思维、直觉思维、合情思维等非逻辑思维以及动手操作能力、创造能力的价值一直没能得到应有的重视，数学课堂很少引导学生进行数学实验和动手操作．一项问卷调查表明[1]：平均每个教师在数学教育中每年仅引导学生作1.12次动手实验，最多的是平均每年5次，最少平均每年0.09次．这种状况，难以达成基础教育课程改革的目标，因而越来越受到教育研究者的重视．

义务教育数学课程标准（2011年版）提出实验也是学生数学学习的一种方式，提倡有条件的学校可以建立数学实验室．虽然大多数教师认为开展数学实验是非常有必要的，但在实践中，数学实验却做得很少．已有研究表明[1~10]：主要原因有3个，一是应试教育压力过重；二是对数学实验的认识不足，怕上数学实验课而影响了教学进度；三是缺乏数学实验的教学经验．正因为有相当一部分教师感到数学教学中很有必要让数学实验进入课堂而又缺乏数学实验的教学经验．基于此，课题组于2009年申报立项江苏省教育科学规划“十一五”重点资助课题“动手‘做’数学——初中数学实验的设计与开发研究”，2012年又申报立项江苏省教育科学规划“十二五”重点资助课题“初中数学实验的理论与实践研究”．历时五年多，对初中数学实验教学的理论与实践进行了系统的探索与研究，旨在为初中数学教师开展数学实验教学提供第一手的实践经验和理论基础．

2 价值及目标定位

通过课题研究，力争在新课程的理念与教师的教学行为之间驾起一座桥梁，体现如下几方面的价值：

（1）转变对数学性质与数学教育价值的认识：数学教育不仅培养学生的理性逻辑思维，它在学生动手实践和创新能力的培养中也发挥着不可或缺的作用．

（2）通过编制《初中数学实验手册》（学生用书）为学生积累“基本数学活动经验”提供载体、建设初中数学实验教学资源库和实验室为学生开展数学实验提供素材与环境，从而实现数学课程标准的目标：积累学生的基本活动经验、为学生提供丰富多彩的学习素材等．

（3）努力转变初中数学教师教的方式与学生学的方式，有效设计和组织数学实验，在理论和实践层面提供可资借鉴的、可供推广的、有价值的研究成果．

课题研究的总体目标定位于：研究梳理数学实验的内容和类型，设计和开发初中数学实验课程，在实践层面提供可借鉴推广的、可操作的研究成果，有效转变初中数学教与学的方式，进一步深化初中数学课程改革．

3 研究过程与方法

过程一：文献研究及现状研究（2009年12月—2010年12月），主要运用文献研究法和问卷调查法，通过文献分析和问卷调查，重在梳理数学实验研究有关文献，把握数学实验的研究现状，研究初中开展数学实验的可行性．

过程二：数学实验课程内容开发（2011年1月—2011年12月），运用文献分析法研读初中数学教材，遴选数学实验素材，并通过实验法，最终确定课程内容，构建初中数学实验课程框架体系，并着手编写《初中数学实验手册》．

过程三：教学实施及效果分析（2012年1月—2013年12月），通过行动研究法，重在研究数学实验在数学教材以及课堂教学中的内容设计开发、表现形态与实施策略，并通过比较法，验证数学实验的教育成效及其优势．

过程四：总结提升及推广辐射（2014年1月—至今），运用经验总结法，发现问题、总结完善、提升理论，编撰实验案例集，出版专著．

4 核心概念界定

由于“数学实验”最先是从大学开始研究的，其定义也大多带有“成人化”的特点．随着数学实验走进了中学，很多教师开始着手研究，并试着结合中学生的特点给数学实验进行了具体化的描述．有的是侧重于问题情境的描述[11]，有的则侧重于操作层面进行描述[12]，也有的从数学建模的视角给出定义[13]，有的综合上面的各个角度进行描述[14]．

另外，类似的定义还有许多，概括起来可以分为两大类，即认识论观点和方法论观点．从认识论角度看，数学实验是人们为获得某种数学理论，检验某个数学猜想，解决某类数学问题，实验者运用一定的物质手段，在数学思维活动的参与下，在典型的实验环境中或特定的实验条件下所进行的一种数学探索活动．从方法论角度看，数学实验是指在一定的数学思想、数学理论的指导下，经过某种预先的组织、设计，借助于一定的（物质）仪器和技术手段，进行数学化（而不是物理化学的）实际操作，包括对客观事物的数量化特性进行观察、抽样、测试、逼近、仿真等，进而解决数学和科学问题的一类科学研究方法．

基于上述两方面的认识，结合初中生认知发展及数学教育的基本特点，课题组将“数学实验”界定为：数学实验是通过动手动脑“做”数学的一种数学学习活动，是学生运用有关工具（如纸张、剪刀、模型、测量工具、作图工具以及计算机等），在数学思维活动的参与下进行的一种以人人参与的实际操作为特征的数学验证或探究活动．它主要着力于学生的学，鼓励学生以类似科学实验的模式进行主动探索．它强调“从做实验中学”，力图通过学生“做实验”的主动探究过程来培养他们的动手实践能力、解决问题的能力和创新精神，积累基本活动经验，进而有效转变初中数学教与学方式．

显然，这里所说的数学实验是数学学习的一种方式，这种学习方式，不是让学生被动地接受教科书上或教师讲授的现成结论，而是让学生从自己已有的“数学经验”出发，变“听数学”为“做数学”，变“看演示”为“动手操作”，变“机械接受”为“主动探究”．

5 开展数学实验可行性调查

在课题研究过程中就初中开展数学实验教学的可行性进行了一次问卷调查．

调查中，课题组研制了“中学数学实验调查问卷”教师卷和学生卷，每个问卷均设置17个问题，包含被调查者的基本信息、对数学教与学的热爱程度和看法、教材中数学实验室栏目的处理情况、对数学实验的了解程度、平时教与学的潜意识中渗透数学实验的做法、通过几个有关数学实验的问题看领悟能力以及是否愿意尝试数学实验教与学等．对问卷调查进行统计分析，得到的初步结论有[15]：

5.1 师生愿意通过动手操作或借助计算机进行探索并解决问题

学生问卷的第9题是“如果现在给你一个尚未解决的问题，可通过动手操作或借助于计算机，让你自己探索，你愿意尝试吗？A．愿意；B．不愿意”，教师问卷的第9题是从教师角度进行设置类似的问题．数据统计图如图1：

图1 学生愿意尝试通过动手操作或借助计算机来解决问题

从统计数据来看，总体上有近90%的学生、96%的教师都非常愿意．女生与男生相比来说更愿意、中等生比其他学生更愿意、高年级学生比低年级更愿意、年轻与年老教师比中青年教师更愿意、县城师生比农村更愿意、教师比学生更愿意式．

5.2 师生愿意尝试数学实验这种教与学的方式

问卷最后一题设置的是是否愿意通过数学实验来进行教与学，其数据统计图如图2、图3：

图2 学生愿意的比例

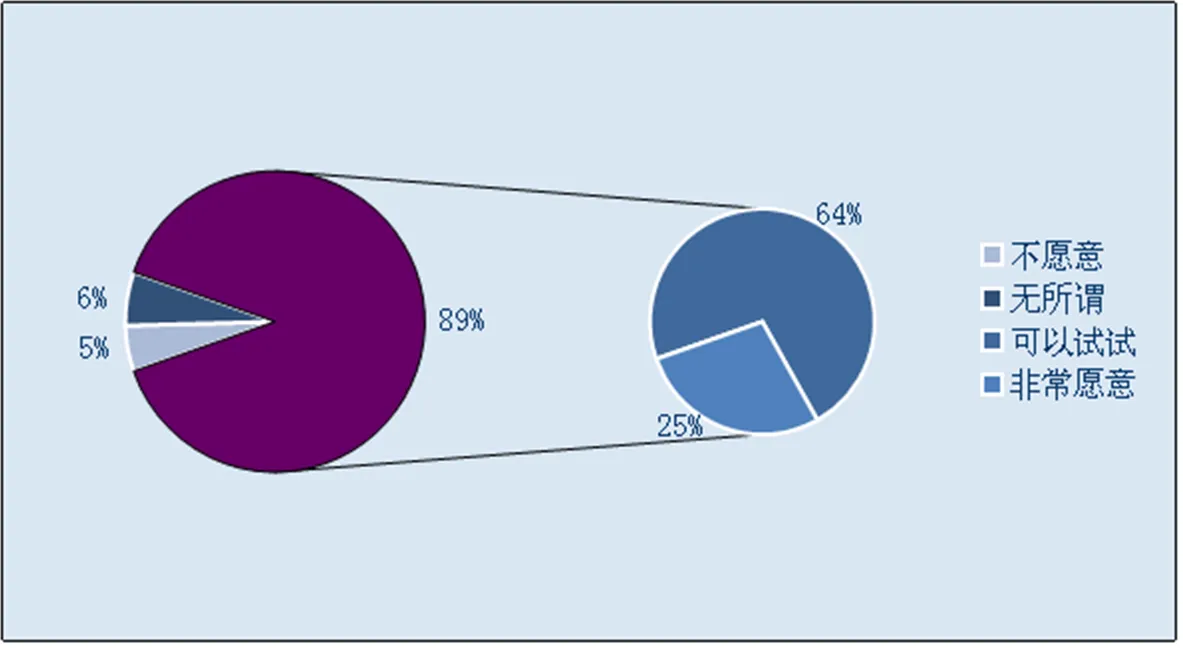
图3 教师愿意的比例

从统计图来看，有89%的学生、94%的教师在了解了数学实验之后，都愿意或非常愿意通过数学实验来学与教．

5.3 师生对数学实验的领悟能力非常高

数学实验对大部分师生来说是比较陌生的，但通过问卷调查显示，他们对数学实验的领悟和理解能力都比较高，这为初中开展数学实验教学奠定了可能性的基础．

问卷中第13、14、15、16题是有关数学实验的领悟和理解的问题．其统计图如图4：

图4 师生对数学实验理解与把握现状的比例

从图4中可以看出，师生对由动手操作揭示数学定理（三角形内角和定理）的准确性还是可以的，教师能正确把握的占69.3%，学生能正确把握的占52.1%；经过引导之后，有13.9%的学生对数学实验“还是不了解”，只有1.4%的教师对数学实验“还是不了解”．

5.4 数学实验教学在初中开展的现状不容乐观

调查统计结果来看，教师在平常教学中渗透数学实验的方式还是偏少的，有34.1%的教师能“借助文具盒模拟两车运动来引导学生思考”；有4.8%的教师能“让学生在计算机上利用《几何画板》画一个三角形进行拖动来发现等腰三角形的性质”；教师上课时对于“数学实验室”的处理“基本没有引导学生动手操作或偶尔让学生通过动手操作来学习”的占83.3%；对于“数学实验课”的开设情况教师回答“从来没开过”或“偶尔进行过片断教学”则高达89.2%．

综上所述，在初中开展数学实验普遍受到师生的欢迎和认可，使得在初中开展数学实验教学有了人力资源保障．同时，数学实验教学要在初中课堂教学中常态化实施还有待时日，需要数学教育专家的引领，需要数学教研工作者的助推，需要广大一线数学教师的自身实践．

6 结论及分析

6.1 数学实验的6种基本类型

初中数学实验，由于其实验的内容、目的以及实验所采取的工具等因素不尽相同，分类的方法与标准也呈现各自的特点．

通过研究，研究者从实验目的和实验所采用的工具两个维度进行考虑，来划分初中数学实验的类型，共可分为6种基本类型[16]．

6.1.1 实物验证型

实物验证型实验，顾名思义是建立在实物直观上的验证型实验．该类数学实验，可以帮助学生通过实验检测、验证已得结论或猜想的正确性，从而在实物直观的基础上获得数学知识的理解．实物验证型实验的显著特点是：直观、思维起点低，操作简单．

6.1.2 实物理解型

实物理解型实验，是借助实物直观，以学生理解数学概念、定理等数学知识为目的的数学实验．此类数学实验通常是在人为干预实验对象的条件下进行的，借助对实物直观的操作，深刻理解数学概念、原理等．实物理解型实验的特点是：实验情境贴近生活，实验过程操作简单，便于学生理解．

6.1.3 实物探索型

实物探索型实验是借助实物直观，以探索未知结论为目的的数学实验．教师创造、模拟、再现问题情境，引导学生自主探究数学知识、发现数学结论（或假设）的学习活动．实物探索型实验的特点是：具有开放性、探索型、生成性，对学生的数学素养、教师的引导方法要求高．

6.1.4 计算机验证型

计算机验证型实验是指，在讲授新课后或问题解决以后，通过计算机操作来进一步验证所原理和结论的正确性的实验．计算机验证型实验的特点是：实验准备省时省力、实验过程简单高效，但要求学生有计算机或数学软件的相关知识做支撑．

6.1.5 计算机理解型

计算机理解型实验往往是基于计算机平台，借助于专门的数学软件，来使学生深刻理解某些不易掌握的数学概念、数学定理，同时增加学生的情感体验，提高学生的学习兴趣，让学生比较快的掌握这些概念和其中的数学思想、数学方法和几何背景．计算机理解型实验的特点是：操作简单、生动高效、需要学生有计算机和数学软件的知识背景．

6.1.6 计算机探索型

计算机探索型实验是借助于计算机（包括图形计算器）的快速运算功能和图形处理功能，模拟再现问题情境，引导学生自主探究数学知识、检验数学结论（或假设）的学习活动．计算机探索型实验的特点是：开放性强、探究性强、对学生的数学素养和计算机技能要求高、对教师的课堂掌控力要求高．

6.2 数学实验设计的基本原则及其要素

任何话语都由基本话语和元话语构成，基本话语侧重于表达概念意义，元话语侧重于表达语篇的意义和人际意义．教学设计也不例外，数学实验课的教学设计既要遵循“目标性、整体性、多样性和简约性”[17]等中观原则外，还要融入微观的经验元素、直观元素、普适元素以及创造元素，方能释放数学实验的内在力量．如果说中观的设计原则是数学实验的基本话语，那么微观的“四个元素”就是其元话语．

6.2.1 数学实验设计的基本原则

一是目标性原则．遵循目标性原则，就是设计者必须事先有目的地设计数学实验的目标、内容、形式、方法、评价等方面的内容，要充分考虑实验内容应达到的目的以及应发挥的作用．遵循初中数学实验的目标性原则，能让实验设计合理，走向正确，形散神聚，符合学生的认知规律和实验潜质．

二是整体性原则．遵循整体性原则，即在实验设计时不能只局限于“一节课”，应以单元甚至章节为基本单位，将目标的设定与操作过程加以分段或分解，在单元甚至更大的整体范围内对某个实验片断的实验目标、内容、方法、策略以及实验方式进行具体的规划、设计与选择．

三是多样性原则．遵循多样性原则，要求所设计的数学实验应呈现出各种不同的类型，以满足不同学生的需要．如有的学生动手能力和观察能力较强，他可能选择动手操作的方式进行实验；有的学生擅长于思考推理，他可能选择演绎推理的方式进行实验；也有的学生计算机水平较高，他可能会借助计算机来进行实验．

四是简约性原则．遵循简约性原则，即指实验设计尽可能采用简单的实验工具或方法，用较少的实验步骤及材料，在较短的时间内完成实验，且效果明显．要求教师在进行数学实验设计时，要尽可能减少实验步骤，秉持“删繁就简”的思想，对实验问题进行分、合、增、删以及适度调整使其简明直白清亮，从而简化操作流程、精简教学环节、减少插话式指令，提高实验载体的高效性、启发性、趣味性、审美性，让实验活动贴近学生思维潜在发展区，经过努力便可操作、易操作、好操作．

6.2.2 数学实验设计的基本元素

一是经验元素．这里的“经验元素”绝非仅指学生已经具备的能力经验，还包括实验背后的预期经验．因此，设计数学实验时必须融入“经验”元素，方能让实验接地气，连人脉．现代课程论指出，有效教学应该以学生的认知发展水平和已有的经验为基础，直面学生主体，因材施教且因材施教．这就从课程意识层面，强调数学实验设计融入经验元素的必要性．

二是直观元素．徐利治先生认为，“只有做到了直观上的懂才算真懂”，裴光亚先生也一再强调“抽象思维的缺位必须借助直观思维来补位”，足见“直观元素”在数学实验设计中的地位不可或缺．由此可见，“直观元素”对理解数学的作用是不容忽视的，这就要求设计实验时必须重视融入直观元素，方显数学实验的教育价值．

三是普适元素．数学实验设计只有从“普适元素”出发，找寻能体现通性、通法以及可以普遍化的实验载体，设计选材精当、方法精准的实验，方能体现数学实验应有的价值．这里的“普适元素”不仅指具有通性、通法的特例，也指具有共性的个例，还指结论的可推广性、延伸性和一以贯之的整体性．

四是创造元素．信念系统（情意要素）对每个人而言是独特的，积极的信念、价值和规条（BVR）是一个人学好数学的情绪地基，而认知信念的状态又取决于教学设计中创造元素的诱发力．这就要求我们设计数学实验时，要渗透创造元素，以此激活信念系统．可以通过精心设计变式问题，引导学生运用合情推理的方法，开展形式多样的探索与猜想活动，揭示数学内在的思想内涵和兴趣因素，建构数学认知背景，激发学生的实验智慧和创造才能．

6.3 数学实验教学的一般模式

从实验前期准备工作量的大与小、实验操作的复杂与简单的程度、实验时间的长与短等方面来说，研究者将数学实验教学分为片段式和专题性两种实验教学形式．

6.3.1 片段式

片段式实验指的是穿插在数学课堂教学中的实验，如根据教学的需要，在数学课程中某一数学主题学习内容前，设置一个与引入主题内容有关的实验情境，在课堂上通过教师的演示或学生的操作，在较短时间内完成的实验．片段式实验可以直接为随后的数学主题服务，通过观察可获得猜想，一般具有启发性、归纳性、直观性，从实验规模上来讲，可以理解为“小实验”．片段式实验又可分为教师演示实验和学生操作实验两种．

教师演示实验，主要针对具体内容，教师通过动手操作教具或软件，用形象、直观的演示（教具或软件的操作），配以清晰的讲解，以实验的方式，将教学的重点、难点用直观的方式表现出来，变抽象的内容为形象、直观的知识，有效地让学生通过观察、分析、思考，理解数学知识．教师演示实验的基本模式是：提出实验主题——教师操作演示——学生观察猜想——验证归纳结论．

学生操作实验，主要指针对具体内容，可由教师事先设计好操作程序，学生再动手操作进行实验．学生在亲自动手操作、经历实验的过程中，能够通过清晰的、直观的看到各种情况的演变，真实地体验、感受到知识的产生、形成过程，这比教师的直接讲解更有说服力，便于理解、记忆和掌握数学知识．当然，实验的最后还可由教师或在实验中获得成功的学生再进行实验的演示．学生操作实验的基本模式是：提出实验内容——学生操作实验——学生观察猜想——验证归纳结论．

6.3.2 专题式

专题性实验指的是围绕一个数学主题组织的专项实验，内容比较丰富、内涵比较深刻．专题性实验需要制定实验计划，要求学生观察现象或记录数据，分组讨论实验中所出现的现象或进行数据分析处理，得出结论，并给出合理的数学解释，最后写出完整的实验报告，就实验中发现的问题尽量做出严格的证明，一般具有探索性、过程性，从实验规模上来讲，可以理解为“大实验”．其模式的操作流程主要包括两个过程：实验过程和验证过程．具体来说，专题实验教学的基本模式可以是：

6.4 数学实验的评价

评价是数学实验开发的关键环节和重要依据，它既是实验活动的相对终结，也是实验活动的持续起点，更是实验活动的循环过程．通过一个阶段的实施情况表明，要提升数学实验的水平，建构数学实验的评价方式、建构学习结果与学习过程并重的评价机制至关重要．

6.4.1 数学实验的评价原则

数学实验评价应遵循整体性原则、发展性原则、适切性原则、过程性原则、多元性原则．

遵循整体性原则，要求在评价中把实验活动、教学和评价进行整合，使它们融合为一个有机整体，贯彻到实验过程中去，将学生在数学实验中的各种表现和活动成果（如活动记录、实验成果、研究报告等）作为评价他们参与活动情况的依据．

遵循发展性原则，要求评价既要考虑学生的过去，重视学生的现在，更着眼于学生的未来，所追求的不是给学生下一个精确的结论，更不是给学生一个等级分数并与他人比较，要通过评价（包括通过分数）促进学生在原有水平上的提高与进步，达到基础教育培养目标的要求．

遵循适切性原则，要求评价必须切合学生实际、切合课程标准．切合学生实际，指确定实验目标从学生的实际出发，能满足大多数学生的需要，也能满足少数水平较高和水平较低学生的需求，而切合课程标准是指实验设计的内容必须切合数学课程标准要求．

遵循过程性原则，要求评价应该揭示学生在活动过程中的表现以及他们是如何解决问题的，而不仅是针对他们是否得出结论．即使数学实验的结果是“失败”的，或者没有得出所谓的“科学”结论，只要学生经历了活动过程，形成了一定的认识，获得了数学活动经验和能力，就应给予学生积极的评价．

遵循多元性原则，要求评价主体、评价方式、评价途径、评价角度以及评价结果的呈现方式的多元化．一方面可以将那些主要的、必不可少的测试结果经过科学处理，转化为标准分数或等级分数，使不同学生经历数学实验的过程具有可比性；另一个方面，教师可视具体的情况和不同任务的性质，采用作品展示、写作数学日记或论文、制作档案资料等多元的表现来展示学生的数学实验活动过程和实验结果．

6.4.2 数学实验的评价内容

数学实验的评价内容有：数学实验内容的评价、学生参与数学实验活动程度的评价合作交流的意识与能力的评价、数学思考与发展水平的评价、发现问题及提出问题和解决问题过程的评价、数学创新能力的评价等．

评价内容要以问题变式的选择性为逻辑起点．乔纳森（D. Jonassen, 1999）等教学论专家强调课堂教学要以问题驱动来组织学习过程，要运用有趣的、真实的问题，帮助学习者形成问题意识．实验教学也不例外，从评价角度来说，要看实验设计是否从问题出发，其问题变式的角度是否广、内涵是否深，能否为学生发现问题、提出问题和分析、解决问题提供行之有效的实验载体和平台．例如，在“搭三角形”实验活动过程中，首先利用准备的学具（长度分别是20 cm、3 cm、4 cm、5 cm、6 cm、7 cm、9 cm的细木棒各1根）让学生任意搭三角形．在操作过程中，势必造成学生的认知冲突，产生追根溯源的迫切感（为什么不能搭？）在这样的迫切解除困惑的心理状态下，一个崭新的概念系渐次明朗（三角形三边的制约关系）．要使既得概念结构化而稳定，必须借助选择性问题变式．为此，实验进入另一流程，要求学生任意将20 cm细棒截为3段，并尝试搭三角形．截棒的过程就是变式理性选择的过程，这就是实验教学的逻辑起点，只有有了这样的逻辑起点，下面的实验才显得有的放矢．

评价内容要以思维落差的突变性为逻辑主线．罗杰斯（C. Rogers, 1983）认为，学习是弥散性（pervasive）的，可以使学生的行为、态度，乃至个性都会发生变化，这里的“弥散性”指思维落差的指数．为此，数学实验教学要以思维落差的高低来评价，以思维落差的突变性水平为评价教学的逻辑主线．低幅度思维落差不能引发思维品质的变化，只有思维落差大的实验教学才能培养高品质的思想．例如，在“折三角形三线”实验活动过程中，依据实验目的，以下3个活动流程思维落差就较为显著：（1）任意取学具箱中的纸片，请折出三角形的3条高，你有什么发现？（2）给一张三角形纸片，过一个顶点，折出面积相等的两部分，你能折出来吗？（3）你能折出过三角形顶点的一条线，满足夹这个角两边之比等于分对边两条线段之比吗？不难发现，第一个活动，存留于操作技术层面，由“画”的技术转化为“折”的技艺，感性思维水平维度持平；第二个活动，融入算法化思想，理性思维水平渐次抬升，判断三角形中线的过程就是数理思维增值的过程；第三个活动，涉及逻辑思维辩证的过程，知性思维水平显著攀升，判断角平分线的过程就是理性精神和人文价值融合释放的过程．

6.4.3 数学实验的评价方法及评价要素

具体的评价方法一般可分为“他评”和“自评”两种．其中“他评”又可分为“教师评”、“学生评”和“家长评”3种．也可以把数学实验分为前期准备、实验过程、总结提炼3个阶段进行评价．前期准备评价要素包括——选择实验主题，查找相关文献资料，制定实验步骤细则并准备实验工具等3个方面．实验过程评价要素包括——小组分工合作的情况，探究思考解决问题的过程，个人的创新之处，运用工具的恰当与否等4个方面．总结提炼评价要素包括——实验报告；数学方法的总结，总结收获、体会，并分析不足；报告的整体感受等4个方面．

历时5年多的实践与探索，除上述的一些问题之外，我们还探索了数学实验的基本特征[18]、数学实验工具的开发问题、数学实验手册的编制与使用问题、数学实验室的标准与建设问题等，另文阐述．当然，数学实验教学还存在诸多的困惑，比如师资培训和教学推广、数学实验教学的模式能否相对定型、数学实验教学的教材如何更加系统化、科学化等．无论对教材、教学还是教师，让数学实验教学从观念变成有助于培养学生创新意识的现实，还需要深入进行研究和探讨．

[1] 孙国良．应开展对数学实验的课题研究[J]．中学数学教学参考，2004，（3）：23-26．

[2] 张晓磊，郭华光．试论数学实验的数学教育功能[J]．数学教育学报，2003，12（2）：38-40．

[3] 彭拯，禹辉煌．论数学实验的数学方法论价值[J]．数学教育学报，2005，14（3）：27-29．

[4] 周玮．融数学实验于高职数学教学的实践与研究[J]．数学教育学报，2010，19（6）：79-81．

[5] 马玉斌．TI图形计算器让数学实验进入课堂教学[J]．数学教育学报，2004，13（3）：85-87．

[6] 常丽艳．中学数学实验课设计范式及其主体认识分析[J]．数学教育学报，2005，14（2）：47-49．

[7] 项昭，贾其锋．基于LOGO技术的中学数学实验及其课程开发[J]．数学教育学报，2005，14（3）：98-100．

[8] 侯立伟．信息技术利于数学实验的开展[J]．数学教育学报，2006，15（1）：99-100．

[9] 尚春虹．数学实验教学的探索与实践[J]．数学教育学报，2002，11（3）：66-68．

[10] 隋鸣，许敏慧．数学实验活动与数学教学[J]．数学教育学报，2004，13（2）：93-95．

[11] 李树臣．论数学实验的教学价值[J]．中学数学（湖北），2009，（11）：1-4．

[12] 张明琴．初中数学实验教学初探[J]．新课程学习（下），2011，（3）：66．

[13] 吴井高．中学开设数学实验课浅论[J]．东西南北：教育，2010，（11）：21-22．

[14] 郑元进．摭谈初中数学实验[J]．中学数学教学参考，2009，（6）：69-71．

[15] 孙朝仁，马敏．开展数学实验的可行性调查与分析[J]．中国数学教育（初中版），2013，（4）：8-12．

[16] 董林伟，魏玉华．浅析初中数学实验的基本类型[J]．中学数学教学参考，2013，（6）：4-7．

[17] 孙朝仁．初中数学实验的基本原则[J]．中学数学教学参考，2013，（8）：15-18．

[18] 董林伟，魏玉华．浅析初中数学实验的基本特征[J]．中国数学教育（初中版），2013，（9）：2-4．

Research on the Theory and Practice of Mathematics Experiment Teaching of Junior Middle School

DONG lin-wei1, SUN Chao-ren2

(1. Teaching Research in Primary and Middle Schools in Jiangsu Province, Jiangsu Nanjing 210013, China; 2. Jiangsu Province Lianyungang City Education Scientific Research Institute, Jiangsu Lianyungang 222006, China)

Mathematical experiment is through a kind of mathematics learning activity to begin to move the brain "doing" mathematics, students use tools (such as paper, scissors, model, measuring tools, drawing tools and computer), a practical operation of everyone involved in the characteristics of the mathematics tests in mathematical thinking activity in the presence of or inquiry activities. Studied early abroad, after entering in twenty-first Century, China began to explore the implementation of middle school, mathematics experiment. In this study, based on the subject of education scientific planning, which lasted 3 years, to the junior middle school mathematics experiment was carried out to study and practice system, content involves mathematics experimental values and goals, concept definition, feasibility study, the basic types, design principles and elements, implement- tation model and evaluation.

mathematical experiment; research; practice

2014–06–04

江苏省教育科学“十一五”规划重点资助课题——动手“做”数学：初中数学实验的设计与开发研究（B-a/2009/01/014）；江苏省教育科学“十二五”规划重点资助课题——初中数学实验的理论与实践研究（B-a/2013/02/083）

董林伟（1965—），男，江苏宜兴人，特级教师，教授级高级教师，主要从事数学教育研究．

G633.6

A

1004–9894（2014）06–0020–06

[责任编校：周学智]