高中生数学焦虑问卷的初步编制

李顺雨，田 澜



高中生数学焦虑问卷的初步编制

李顺雨1，田 澜2

（1．郑州升达经贸管理学院 建筑工程系，河南 郑州 451191；2．湖北师范学院 教育科学学院，湖北 黄石 435002）

在文献回顾、专家访谈及理论构建的基础上，编制了“高中生数学焦虑问卷”，并对湖北省430名高中生进行施测．结果表明：高中数学焦虑归并为课堂学习过程焦虑、课外解题自我监控焦虑和应考情景焦虑3个维度；全问卷的内部一致性系数为0.90，各分问卷的信度均在0.82以上．“高中生数学焦虑问卷”是一个有效地测量高中生数学焦虑的工具．

高中生；数学焦虑；问卷

1 引 言

近半个世纪以来，数学焦虑研究成为了心理学和教育学研究者关注的重要领域之一．众多研究表明数学焦虑是影响数学成就（mathematics achievement）的关键因子，例如：Abu-Hilal[1]报告，中学生的数学焦虑与数学成就之间呈-0.93的显著性负相关．Birgin等人[2]研究发现，中学生各年级的数学焦虑与数学成就之间的负相关显著，相关系数为-0.75~-0.69．此外，数学焦虑还影响着中学生的自我管理（self-regulation）、自我效能感（self-efficacy）及生涯效能感（career efficacy）等．例如：Jain和Dowson[3]调查显示，中学生数学焦虑与其自我管理能力、自我效能感之间呈现显著性负相关．Lavasani等人[4]研究得出，高一男生的数学焦虑与自我管理、自我效能感之间负相关显著．Scarpello[5]分析表明，数学焦虑和生涯效能感之间成负相关，高数学焦虑的学生将来可能避开与数学相关的课程和职业．毋庸置疑，缓解学生的数学高焦虑自当成为促进他们的数学成就，提高其自我管理能力、自我效能感及职业效能感的重要举措．然而通过文献检索发现，国内新近才出现关于数学焦虑方面的研究，且已有研究多集中在文献综述上，关于数学焦虑的实证调查相对较少，考察高中生数学焦虑的研究更为鲜见．众所周知，与初中相比，高中的数学学习内容、数学学习方法、数学学习环境等都发生了巨大变化，这极易诱发高中生消极的数学学习心理，比如害怕数学、逃避数学、对数学的学习产生焦虑等．已有调查发现，当前中国高中生的数学焦虑普遍存在．例如，彭乃霞等人[6]报告，有26%的高中生存在低度和高度焦虑．熊建华[7]研究发现具有严重和轻度数学焦虑水平的中学生总和竟达48%．但由于所用工具的不同，目前尚未建立中国高中生数学焦虑的流行率．

在西方，数学焦虑测量工具的开发最初是基于一线数学教师对数字焦虑的观察．Dreger和Aiken[8]在1957年开发出了第一份测量数学焦虑的问卷即“数字焦虑问卷”，但是该问卷缺少实证的信效度证据．随后Richardson和Suinn[9]扩大了数字焦虑的内涵，在1972年提出了数学焦虑的定义并编制了包含98个题目的数学焦虑等级量表（The Mathematics Anxiety Rating Scale，简称MARS）．该问卷因具有较高的信、效度[10~11]而成为数学焦虑研究中运用最多的问卷之一．后来，MARS被拓展成几种不同的版本，比如：不仅有青少年数学焦虑等级量表（Mathematcs Anxiety Rating Scale for Adolescents，简称MARS-A）[12]和小学生数学焦虑等级量表（The Mathematics Anxiety Rating Scale for Elementary School Students，简称MARS-E）[13]等，而且针对题目过多，测试起来费时费力等不足，学者们还开发有简化版的MARS[10~11，14~15]．除MARS之外，西方比较常用的数学焦虑量表还有Fennema和Sherman编制的数学态度量表（Fennema-Sherman Mathematics Attitudes Scales，简称MAS）[16]以及Wigfield和Meece编制的数学焦虑问卷（The Math Anxiety Questionnaire，简称MAQ）[17]等．

值得注意的是，由于两方面的主要原因，西方已有数学焦虑量表的推广受到了限制：一是各国学生的数学课程学习均具有本土的教育制度和地域文化特点[18~21]，因而国家不同其数学学习结果也不尽相同．如：2009年经济合作与发展组织进行的第四次国际中学生评估项目测试得出中国学生的数学平均成绩（600分）远高于美国学生（487分）．用专门针对美国学生而编制的数学焦虑问卷未必能准确地测查出中国学生数学焦虑的实际水平，简单照搬自然会改变问卷的性能．黄大庆等人在编制“高中数学焦虑量表”[22]时，直译测查大学生的MARS问卷调查中国高中生，探索性因素分析析取的因子内容远远偏离了原理论，因素分析所显示该问卷的性能指数也大为降低．针对MARS存在的文化适应性问题，一些国家的学者开发了本土的数学焦虑问卷，例如：韩国Ko和Yi研制的学生数学焦虑量表（Mathematics Anxiety Scale for Students，简称MASS）[23]．遗憾的是，目前尚未检索到中国本土化的数学焦虑量表．其二，已有数学焦虑量表大都是针对大学生研制的（比如；MARS、中文版MAS[24]），专门针对高中生的版本较少．鉴于此，有必要编制一份既具有较好信效度，又符合中国高中生数学学习实情的数学焦虑问卷．

2 方 法

2.1 高中生数学焦虑的界定及理论维度的构建

数学焦虑的实质为何？目前主流的看法比较倾向于“状态焦虑”，即在特定情境下所产生的专门反应状态．但在界定数学焦虑的性质和范畴时，学者们又各有侧重．比如：Richardson和Suinn将数学焦虑界定为“在各种类型的一般生活和学业情境中，阻碍数字控制和数学问题解决的紧张和焦虑感觉”[9]．Cemen认为数学焦虑是那些威胁自尊的数学情境做出反应的焦虑状态．陈英和和耿柳娜[25]则把数学焦虑理解为个体在处理数字、使用数学概念、学习数学知识或参加数学考试时所产生的不安、紧张、畏惧等焦虑状态．基于“状态焦虑”取向，这里将高中生数学焦虑界定为：高中生是一般学习焦虑在数学学习情境中的具体表现，尤指高中生在数学课堂听讲、数学课外解题与复习、数学应试等主要学习环节中所体验到的担忧、紧张或不安等焦虑状态．

由于在数学焦虑内涵的理解上存在分歧，对于数学焦虑究竟应该包含哪些成分，学者们的看法不太一致．表1呈现的是已有问卷所包含的数学焦虑的结构成分．鉴于尚无公认的数学焦虑的理论结构模型，这里拟从3个方面来考虑数学焦虑的模型建构：一是高中生数学焦虑的操作性定义，问卷主要测查高中生在主要学习情景中的状态焦虑．二是吸收已有量表在维度建构中的合理成分，从表1可以看出，已有数学焦虑量表均涉及了考试方面的焦虑内容，更有研究者拿考试焦虑来直接评估学生的数学焦虑水平，因而把考试焦虑纳入到理论维度之中．三是考虑到高中数学教学实践上的针对性和可操作性．高中生数学焦虑主要是高中生在数学学习过程中所产生的，具有很强的针对性和情景性，那些偏离学校数学学习情景的因子，针对性就较差（如：MASS的生活焦虑维度），在测查中难免会遇到麻烦．例如：RMARS量表中的数学过程焦虑维度和数学考试焦虑维度有交叉，而高中生数学焦虑量表中的观察焦虑也可以在生活焦虑中体现．因此，高中生数学焦虑应该测查高中主要学习情景中的焦虑反应，而高中生主要的学习情景包括3部分：知识的习得过程（数学课堂听讲）、知识保持过程（数学课外解题与复习）、知识应用过程（数学应试）．基于上述考虑，提出高中生数学焦虑的“3因素模型”，即高中生数学焦虑包括课堂学习过程焦虑、课外解题自我监控焦虑和应考情景焦虑．

表1 已有的数学焦虑问卷的结构成分一览表

2.2 问卷题目的初步确定

首先就问卷的操作性定义和3维度结构，咨询8名教育专家（博士或教授），总体赞同率达到87.5%．接着使用教师访谈调查，采集问卷题项．抽取湖北省黄石市35名高中数学教师（其中重点高中教师20人，普通高中教师15人），请他们在研究者提供的开放式问卷上，罗列高中生在“课堂学习过程焦虑”、“课外解题自我监控焦虑”和“应考情景焦虑”3个维度上的数学焦虑体验表现．研究者对教师的访谈结果加以整理和分析，选择有代表性和普遍性的条目，构成初始问卷的主要项目，再经过5名黄石市高中数学教研员逐条讨论，经适当补充、删减、修改和归并．继之，请两位教育心理学博士逐题项审查了问卷的表面效度，从而编制了22个项目的高中生数学焦虑问卷．问卷各项目用5点记分法，即感到没有焦虑记1分、感到有点焦虑记2分、一般焦虑记3分、感到比较焦虑记4分、感到非常焦虑记5分．被试在问卷上的得分越高，则说明其数学焦虑水平越高．

2.3 对 象

采用整群分层取样的方法，选取黄石市第七高级中学的高一、高二各4个班级的460名学生为研究对象．以班级为单位进行调查，回收有效问卷430份（按奇偶编号分为样本一和样本二，分别用于探索性因素分析和验证性因素分析）．其中男生233名（占54.2%），女生197名（占45.8%）；高一164名（占38.1%）、高二266名（占61.9%）；农村和城镇来源学生分别为307名（占71.4%）和123名（占28.6%）．

2.4 施 测

采用统一的指导语进行整班施测，施测时间约为20分钟，问卷当场回收．共发放问卷460份，回收460份，回收率为100%．

2.5 统计分析

对有效问卷按照随机编码的奇偶性分成两半，对奇数号数据（样本一，=215），运用SPSS 16.0做探索性因素分析，析取高中生数学焦虑的主要成分，对偶数号数据（样本二，=215），用Amos17.0做验证性因素分析．

3 结 果

3.1 探索性因素分析

首先，计算22个题项与总分的相关，结果所有题目与总分的相关都大于0.4．其次，对22道题目进行第一次探索性因素分析，KMO系数0.914，Bartlett球形检验统计量为2.61（=231，<0.001），可提取特征根大于1的4个因子，共解释63.270%．删除在多个因素上均有较高负荷的V3、V6、V14、V21及不符合主观因素构想的题项V1、V7、V9、V10、V17，最后剩下13个题目．

对剩下的13道题目进行第二探索性因素分析，KMO系数0.903，Bartlett球形检验统计量为1.30（=78，<0.001）．可提取特征根大于1的3因子，共解释66.70%．第二次探索性因素分析结果显示13个项目的负荷都大于0.40．对这13个题项进行正交旋转，得出旋转因素负荷矩阵，并根据以下标准确定因子数目：（1）因素的特征值大于等于1；（2）因素必须符合陡阶检验；（3）抽出的因素在旋转前至少能解释2%的总变异；（4）每个因素至少包含3个题项；（5）因素比较好命名．根据以上原则，最终选择3个因素，每个因素的特征值、贡献率及累计解释率见表2．

表2 各个因素的“特征值”“贡献率”“累积解释率”

根据各个因素所包含题目的含义，将所提取的因素命名为：课外解题自我监控焦虑、应考情景焦虑和课堂学习过程焦虑．第一因素包含5个题项，且题目涉及“在数学复习中，当你无法集中注意力时”、“在做数学课外作业的过程中，当你看不懂题目意思时”、“在数学复习中，当你发现有同学干扰你时”等有关课外解题自我监控的焦虑，因此命名为“课外解题自我监控焦虑”；第二个因素包含4个题项，项目涉及“当你想到一小时之后即将到来的数学考试时”、“当你想到五分钟之后即将到来的数学考试时”、“当你即将参加数学月考时”等内容，命名为“应考情景焦虑”；第三个因素4个题项涉及的是“在数学课堂上，当老师在讲解教材上的例题时所感受到的焦虑”、“在数学课堂上，当老师在讲解数学试卷时所感受到的焦虑”等有关数学课堂学习过程的焦虑，因此命名为“课堂学习过程焦虑”．

3.2 问卷的结构验证

采用AMOS17.0软件进行验证性因素分析，通过模型确定对实际数据的拟合程度，拟合指数见表3，因子结构模型及标准化路径系数如图1所示．

表3 高中生数学焦虑3个因子模型拟合指标

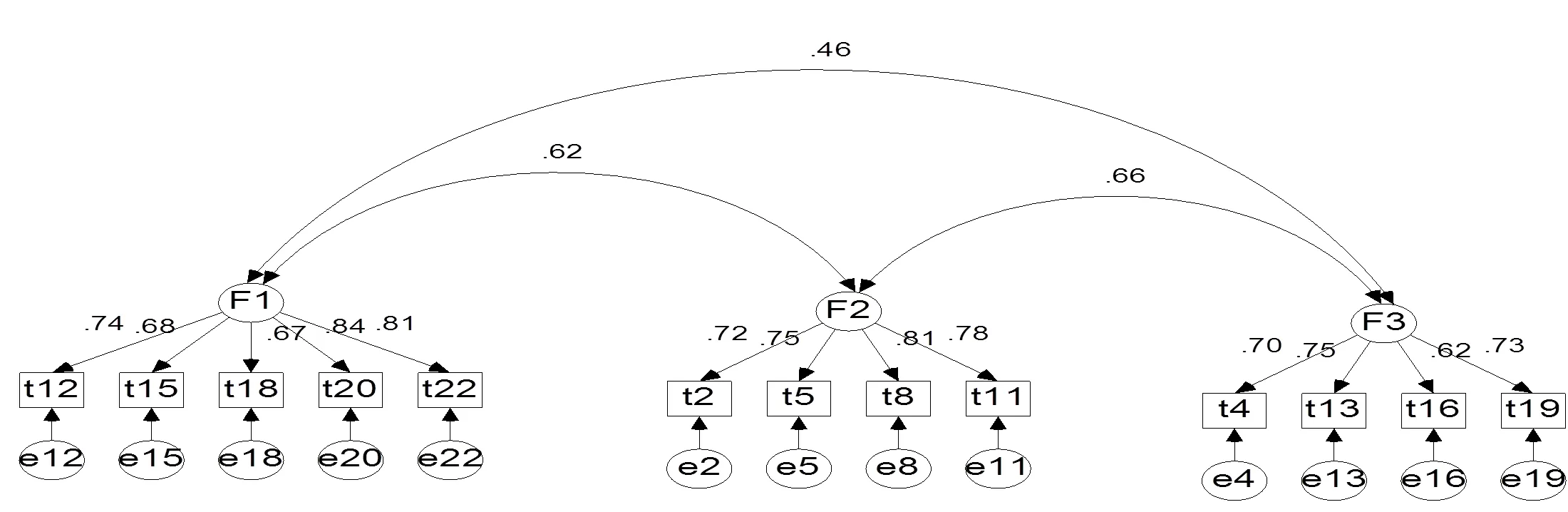
图1 高中生数学焦虑三因素的标准化路径图

由表3可知，在高中生数学焦虑模型中2/小于3，IFI、CFI、TLI、NFI都大于0.90，而RMSEA小于0.08，各项指标均达到可接受的水平，说明该模型拟合度较好．

3.3 问卷的信度检验

分析自编高中生数学焦虑问卷的同质性信度，表4显示，总问卷的内部一致性系数为0.90．3个分问卷的内部一致性信度系数和分半信度系数分别为0.82~0.86和0.80~0.82，总问卷及各分问卷的信度系数均较好地满足了心理测量学的要求．

表4 高中生数学焦虑的信度

3.4 问卷的效度检验

3.4.1 结构效度

表5显示，问卷各因素得分与总分的相关为0.79~0.85，各因素得分之间的相关系数为0.46~0.56．另外，探索性因素分析的结果表明，抽取的3个因素可以解释项目总变异的66.70%，因素分析的结果基本符合最初对量表结构的理论构想．

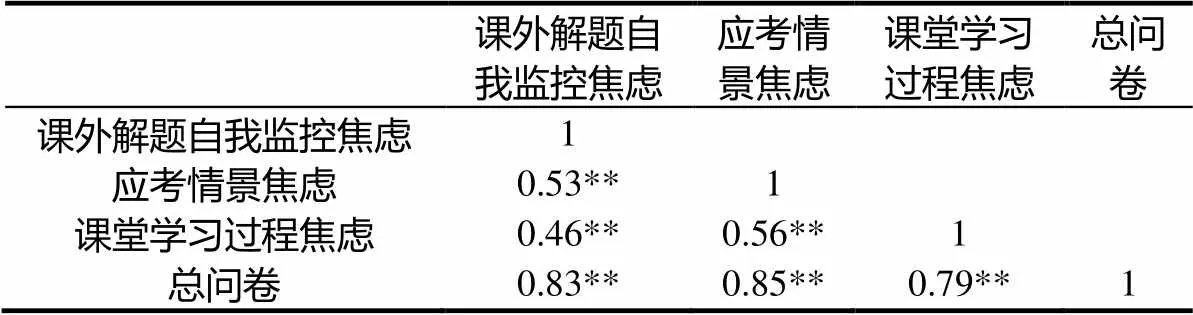
表5 各因素及其与总分的相关矩阵

注：**＜0.01

3.4.2 预测效度

“高中生数学焦虑问卷”的施测是在期末考试的前两周进行的，抽取了该样本在期末考试中的数学成绩，删除未填写姓名的问卷（问卷姓名填写采用自愿原则）和未参加数学考试的学生218人，最终剩下212名学生（高一76人，高二136人；男生136人，女生76人）．计算高中生数学焦虑总分对学习成绩的预测效度．结果表明高中生数学焦虑总分与数学成绩呈显著性负相关，相关系数为-0.311（<0.01）．

4 讨 论

在编制高中生数学焦虑问卷过程中，充分考虑高中生的数学焦虑实情，选取高中生对数学焦虑的典型行为表现，构成初试问卷的基本条目．分析表明，问卷具有较好的信度和效度．首先，经筛选后的13个项目构成的问卷内部一致性系数为0.90，分问卷的信度均在0.82以上，显示该问卷有较好的可靠性．其次，该问卷也有较好的结构效度和预测效度．问卷各因素与总问卷呈现偏高的相关（0.79~0.85），说明高中生在数学焦虑各维度上的反应具有一致性；各因素间呈中等相关（0.46~0.56），则表明各因素之间又具有一定的独立性，验证性因子分析的结果显示“高中生数学焦虑问卷”的IFI、CFI、TLI、NFI、RMSEA等拟合指数较好，而且被试数学焦虑总分与数学成绩之间呈现-0.311的显著性负相关．因此，自编的“高中生数学焦虑问卷”具有较为理想的结构效度和预测效度．

在建构问卷的理论框架时，在参照问卷的操作性定义及国内外相关理论和同类研究结构的同时，还结合中国高中生数学焦虑方面的有关内容，从课外解题自我监控焦虑、应考情景焦虑与课堂学习过程焦虑3个维度建构高中生数学焦虑的结构模型．最终，探索性因素分析结果显示，析取了课外解题自我监控焦虑、应考情景焦虑与课堂学习过程焦虑3个因子．

5 结 论

（1）高中生数学焦虑的结构包括课外解题自我监控焦虑、应考情景焦虑和课堂学习过程焦虑3个维度．

（2）自编的“高中生数学焦虑问卷”具有良好的信、效度，说明问卷适合作为测评高中生数学焦虑的工具．

[1] Abu-Hilal M M. A Structural Model for Predicting Mathematics Achievement: Its Relation with Anxiety and Self-Concept in Mathematics [J]., 2000, 86(3): 835-847.

[2] Birgin O, Baloğlu M, Çatlıoğlu H, et al. An Investigation of Mathematics Anxiety among Sixth Through Eighth Grade Students in Turkey [J]., 2010, 20(6): 654-658.

[3] Jain S, Dowson M. Mathematics Anxiety as Function of Multidimensional Self-Regulation and Self-Efficacy [J]., 2009, 34(3): 240-249.

[4] Lavasani M G, Hejazi E, Varzaneh J Y. The Predicating Model of Math Anxiety: the Role of Classroom Goal Structure, Self-Regulation and Math Self-Efficacy [J]., 2011, (15): 557-562.

[5] Scarpello G V. The Effect of Mathematics Anxiety on the Course and Career Choice of High School Vocational- Technical Education Students [D]. Drexel University, 2005.

[6] 彭乃霞，廖爽，吴现荣．贵州民族地区高中生数学焦虑成因调查分析与研究[J]．数学通报，2010，（5）：14-17．

[7] 熊建华．中学生数学焦虑及相关因素的调查研究[J]．数学教育学报，2008，17（3）：52-54．

[8] Dreger R M, Aiken L R. The Identification of Number Anxiety in a College Population [J]., 1957, 48(6): 344-351.

[9] Richardson F C, Suinn R M. The Mathematics Anxiety Rating Scale: Psychometric Data [J]., 1972, 19(6): 551-554.

[10] Suinn R M, Winston E H. The Mathematics Anxiety Rating Scales, a Brief Version: Psychometric Data [J]., 2003, 92(1): 167-173.

[11] Hopko D R, Mahadevan R, Bare R L, et al. The Abbreviated Math Anxiety Scale (AMAS) Construction, Validity, and Reliability [J]., 2003, 10(2): 178-182.

[12] Suinn R M, Edwards R. The Measurement of Mathematics Anxiety: The Mathematics Anxiety Rating Scale for Adolescents—MARS-A [J]., 1982, 38(3): 576-580.

[13] Suinn R M, Taylor S, Edwards R W. Suinn Mathematics Anxiety Rating Scale for Elementary School Students (MARS-E): Psychometric and Normative Dada [J]., 1988, 48(4): 979-986.

[14] Plake B S, Parker C S. The Development and Validation of a Revised Version of the Mathematics Anxiety Rating Scale [J]., 1982, 42(2): 551-557.

[15] Alexander L, Martray C R. The Development of an Abbreviated Version of the Mathematics Anxiety Rating Scale [J]., 1989, 22(3): 143-150.

[16] Fennema E, Sherman J A. Fennema-Sherman Mathematics Attitudes Scales: Instruments Designed to Measure Attitudes toward the Learning of Mathematics by Females and Males [J]., 1976, 7(5): 324-326.

[17] Wigfield A, Meece J L. Math Anxiety in Elementary and Secondary School Students [J]., 1988, 80(2): 210-216.

[18] 曹一鸣，王立东，Paul Cobb．美国统一州核心课程标准高中数学部分述评[J]．数学教育学报，2010，19（5）：8-11．

[19] 曾宪林．加拿大高中数学课程标准和教学评价的启示[J]．数学教育学报，2011，20（3）：87-89．

[20] 王奋平．中英高中数学教材比较研究——以英国AQA考试委员会与北师大版高中数学教材平面向量为例[J]．数学教育学报，2011，20（6）：51-55．

[21] 叶立军，王晓楠．中美高中数学教材比较研究——以“几何概型”为例[J]．数学教育学报，2012，21（2）：49-52．

[22] 黄大庆，张日昇，陈英和．高中生数学焦虑的结构和量表编制[J]．中国临床心理学杂志，2008，（2）：144-145．

[23] Ko H K, Yi H S. Development and Validation of a Mathematics Anxiety Scale for Students [J]., 2011, 12(4): 509-521.

[24] 张帆，祝振兵．中文版数学焦虑量表的信度和效度研究[J]．数学教育学报，2011，20（4）：59-62．

[25] 陈英和，耿柳娜．数学焦虑研究的认知取向[J]．心理科学，2002，（6）：653-655．

[26] Rounds J B, Hendel D D. Measurement and Dimensionality of Mathematics Anxiety [J]., 1980, 27(2): 134-149.

附录——“高中生数学焦虑问卷”维度及项目组成

维度一：课外解题自我监控焦虑维度（包含5个题项）

12. 在做数学课外作业的过程中，当你看不懂题目意思时．

15. 在数学复习中，当你发现有同学干扰到你时．

18. 当你不能在规定的时间内完成数学课外作业时．

20. 在数学复习中，当你无法集中注意力时．

22. 在数学复习中，当你感到毫无头绪时．

维度二：应考情景焦虑维度（包含4个题项）

2. 当你想到一小时之后即将到来的数学考试时．

5. 当你想到五分钟之后即将到来的数学考试时．

8. 当你即将参加数学月考时．

11. 当你即将参加数学期中考试时．

维度三：课堂学习过程焦虑维度（包含4个题项）

4. 在数学课堂上，当老师在讲解教材上的例题时所感到的焦虑．

13. 在数学课堂上，当老师在讲解数学试卷时所感到的焦虑．

16. 在数学课堂上，当老师在讲解数学课外作业中的错题时所感到的焦虑．

19. 在数学课堂上，当老师要求分小组讨论问题时所感到的焦虑．

Development of Mathematics Anxiety Questionnaire for High School Students

LI Shun-yu1, TIAN Lan2

(1. Department of Architectural Engineering, Shengda Trade Economics & Management College of Zhengzhou University, Henan Zhengzhou 451191, China; 2. College of Education Science, Hubei Normal University, Hubei Huangshi, 435002, China)

Upon literature review, in-deep interview with experts and theoretical construction, a new mathematics anxiety questionnaire for high school students (MAQ-HSS) was developed and used for 460 high school students. Results: The MAQ-HSS consists of three dimensionalities, which can be nominated learning-process anxiety in class, self-monitoring anxiety of solving extracurricular problems, situational anxiety of coping with examination; The internal consistency coefficient of total scale was 0.90. The reliability of each scale was above 0.82. The MAQ-HSS can be used to assess high school students’ mathematics anxiety.

high school students; mathematics anxiety; questionnaire

G620

A

1004–9894（2014）06–0063–05

2014–07–07

李顺雨（1987—），男，河南睢县人，主要从事发展与教育心理学研究．本文通讯作者田澜．

[责任编校：周学智]