有阻尼智能弹簧减振系统参数的一种设计方法

倪 德，朱如鹏，陆凤霞，付秋菊，鲍和云

（南京航空航天大学机电学院江苏省精密与微细制造技术重点实验室，南京 210016）

有阻尼智能弹簧减振系统参数的一种设计方法

倪 德，朱如鹏，陆凤霞，付秋菊，鲍和云

（南京航空航天大学机电学院江苏省精密与微细制造技术重点实验室，南京 210016）

研究简谐激励下有阻尼智能弹簧减振系统参数的一种设计方法，使系统能同时实现阻尼与刚度控制。首先，利用等效线性化方法得到系统频响特性的的解析解。然后，分析了系统参数对幅频特性的影响，得到如下结论：系统无粘性阻尼时，幅频特性曲线簇有一个公共点，有阻尼时公共点消失；影响系统幅频特性的主要参数为质量比、刚度比、阻尼比和控制参数；阻尼比和相对阻尼比影响系统实现完全耦合时所需作动力的大小。最后，根据参数分析的结论，确定系统参数的选用范围，并给出系统参数设计的方法和步骤。

参数设计；减振；智能弹簧；压电陶瓷；干摩擦；刚度；阻尼

主动减振技术依靠外部能量可调节系统参数，不仅对中高频段有效，而且对被动减振技术无能为力的低频段也有效［1－2］，从而受到人们的广泛关注。由于适应系统变化的能力强，近几十年来，基于压电陶瓷等智能材料的主动减振技术倍受学者们的青睐［3－5］。然而绝大多数基于压电陶瓷的主动减振技术是通过直接抑制激励力的方式进行减振的，对压电陶瓷作动器（PZTA）的驱动电压和输出位移要求较高。智能弹簧减振系统由两个弹簧－质量系统并联而成，通过PZTA动作产生的微位移将二者联系在一起，以改变系统结构参数这样一种间接的方式来减小系统振动的传递。与直接抑制激振力的方式相比，它不需要复杂的位移放大装置和很高的驱动电压，更易于实现［6－7］。因此，此类型的减振装置具有很好的研究意义。

Wickramasinghe等［6－10］以直升机旋翼转子的扭转振动为应用对象，对智能弹簧减振技术的减振性能、控制策略与算法、台架试验和风洞试验等方面做了较深入的研究。Afagh等［11］研究了装有智能弹簧的直升机旋翼转子的建模与稳定性分析方法。Coppotelli等［12］通过试验研究了智能弹簧作动器的模态特性，通过模态参数的分析展示了智能弹簧改变直升机桨叶动态行为的能力。Cavalini等［13］提出使旋转机械能安全跨越临界转速的智能弹簧半主动减振技术。范天宇等［14］提出的弹性支承干摩擦阻尼器利用动静摩擦片之间的摩擦为转子系统提供阻尼，降低通过临界转速时的转子振动。王四季等［15－16］在此基础上发展了主动式弹支干摩擦阻尼器，利用电磁铁控制动、静摩片之间的接触、分离和压力，主动控制阻尼器附加到转子系统的阻尼和支承刚度，减振效果良好，原理与智能弹簧概念有些相似。

智能弹簧减振系统采用PZTA作为控制元件，应用时PZTA的尺寸受到限制，控制电压施加范围有限，只有对系统参数进行合理设计和选用后，才能达到较好的减振效果，而目前鲜见相关文献报道。所以，本文针对简谐激励下的单级有阻尼智能弹簧减振系统，在充分分析系统参数与响应之间关系的基础上，提出了一种智能弹簧系统参数的设计方法。研究结果为智能弹簧减振系统的分析与设计提供了理论参考。

1 智能弹簧减振系统的频响特性

图1 智能弹簧减振系统模型Fig．1 Model of Smart Spring vibration suppression system

1.1 系统的模型与运动方程

智能弹簧减振系统由基本弹簧k1、主动弹簧k2和PZTA等组成，其物理模型如图1所示，结构下端固定于基础之上，上端承受外部激励F（t）。基本弹簧与主动弹簧平行布置，其内部阻尼系数分别为c1和c2。m1为与基本弹簧相联的振动结构的等效质量，m2为与主动弹簧相联的PZTA的集中质量。基本弹簧－质量系统为主系统，主动弹簧－质量系统为辅助系统。PZTA与主系统之间有一初始间隙δ，PZTA不工作时，辅助系统与主系统分离，不参与振动。给PZTA施加控制电压后，PZTA产生微位移s，当s＞δ时，PZTA将在主系统上产生作动力N（t），随主、辅系统之间的相对运动形成滑动摩擦力Fd，辅助系统为主系统提供振动阻尼，称为阻尼控制。由于干摩擦的粘滞效应，主、辅系统随控制电压的增大而逐步耦合到一起。当控制电压足够大时，二者完全耦合，若耦合系统的固有频率远大于主系统固有频率称为刚度控制；若耦合系统的固有频率远小于主系统固有频率称为质量控制［6］。

智能弹簧减振系统的振动微分方程可表示为

rds质量控制方式在实际系统中难以实现，因此智能弹簧减振系统采用阻尼和刚度控制方式。当vr≠0时为阻尼控制，当vr＝0时为刚度控制。

由式（1）可知，智能弹簧减振系统中含有表征为分段函数的干摩擦环节，为强非线性系统，很难直接获得系统响应的解析解［17］。已有很多学者对干摩擦系统的计算与分析问题作了研究［18－19］。然而本文的目的不在于研究系统精确的动力学行为，所以采用线性模型对其进行逼近，以便于解析研究，即采用等效粘性阻尼表征干摩擦的非粘性阻尼效应［20］。

假设系统受简谐激励F（t）＝f0sinωt，则

等效粘性阻尼系数Ceq为

1.2 阻尼控制时系统的频响特性

对式（5）进行求解，得到系统的的频响特性为

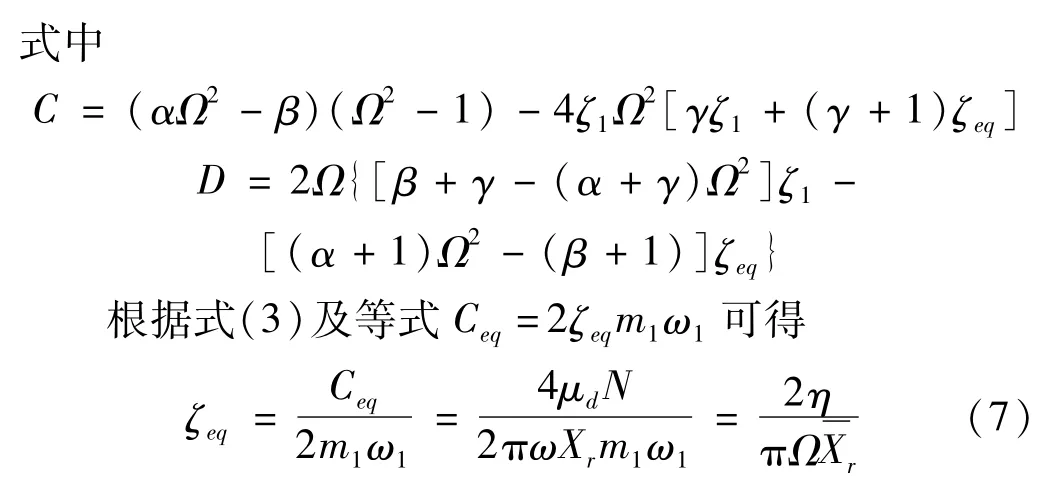
由式（2）可知，辅助系统的稳态响应为

1.3 刚度控制时系统的频响特性

当ζeq为虚数时，表示辅助系统的反作用力不能克服静摩擦力，辅助系统随主系统一起运动，成为单自由度系统，即刚度控制方式下系统的运动微分方程为

2 系统参数对幅频特性的影响

由上节的分析可知，影响智能弹簧系统幅频特性的量纲一系统参数如下（具体定义参见1．1节）：

首先，取系统参数为：α＝0．1，β＝1．5，ζ1，γ＝0，得到不同控制参数η下系统的幅频特性曲线如图2（文中所有图形直接用X1表示）。图2中，幅频特性曲线组成的曲线簇通过一个公共点p，对应的频率比为Ωp＝1．291；存在一最优控制参数ηopt＝1．084，使系统幅频特性曲线取得最小峰值（X1，max＝1．5），且峰值点对应频率比恰好在公共点p位置；在达到ηopt之前，系统幅频特性曲线峰值随控制参数η的增大而减小，体现为等效阻尼比ζeq在增大；而达到ηopt之后，系统幅频特性曲线峰值反而随着控制参数η的增大而增大，体现为等效阻尼比ζeq在减小。若η＜π／4，在共振频率Ω＝1位置，幅频特性曲线峰值趋向于无穷大，原因是干摩擦阻尼消耗的能量远小于系统输入的能量。所以，为使智能弹簧装置能有效控制系统共振峰值，需保证η＞π／4。图2表明，随控制参数η的增大，系统出现粘滞的频率区间变大（即主、辅系统逐渐耦合在一起）；虚线部分表示控制参数η大到足以使辅助系统与主系统间不存在相对滑动而完全耦合成一单自由度系统。可见，刚度控制方式可以避开主系统共振频率，使主系统的共振幅值急剧下降，但同时会出现新的共振点。

表1 影响智能弹簧系统频响特性的系统参数Tab.1 System parameters which affect the frequency response characteristics of smart spring system

图2 控制参数η对系统幅频特性的影响Fig．2 Influence of control parameter η on the amplitude frequency characteristics of system

增大质量比α为0．4，其他参数不变，其幅频特性曲线如图3。图3表明，增大质量比α，幅频特性曲线簇的公共点向左移（Ωp＝1．208）；系统的最佳η值减小（ηopt＝1．01），而最小峰值增大（X1，max＝2．181 9）；刚度控制下的耦合系统与主系统的固有频率更加靠近，耦合系统的共振区变窄，共振峰陡峭，且当η＞π／4后，幅频特性曲线的峰值都有所增大。取质量比α为横坐标，对应的幅频特性曲线峰值为纵坐标，可得图4。图4表明，质量比α与刚度比β的取值相差越大，幅频特性曲线峰值越小，而当α＝β时，辅助系统的固有频率与主系统相等，使得幅频特性曲线峰值趋向于无穷大。可见，为获得较好的减振效果，质量比α的取值要求比刚度比β的取值大得多或小得多。然而质量比α取值大于刚度比β时，会使得耦合系统的固有频率小于主系统的固有频率，不符合实际需求，所以未给出α＞β的情况的图形（关于直线α＝β对称）。

图5表明，系统无粘性阻尼时（ζ1＝0，γ＝0），增大刚度比β，幅频特性曲线簇的公共点向右移（Ωp＝1．35）；通过大量数值计算发现，刚度比β的变化不会改变ηopt值的大小，但会减小最小峰值（X1，max＝1．235 3）；刚度控制下耦合系统与主系统的固有频率变得远离，耦合系统的共振区变宽，共振峰平坦，且当η ＞π／4后，幅频特性曲线峰值降低。如图6，刚度比β与质量比α相差越大，系统幅频特性曲线峰值越小，且当二者的差距达到一定程度时，峰值基本保持不变，与图4类似。

图3 质量比α＝0．4时系统的幅频特性曲线Fig．3 Amplitude frequency characteristic curves of system while mass ratio α＝0．4

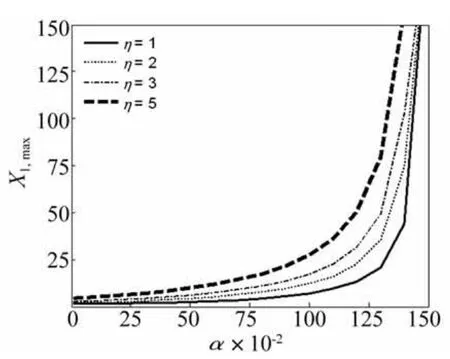
图4 质量比α对系统幅频特性峰值的影响（β＝1．5）Fig．4 Influence of mass ratio α on the peak value of amplitude frequency characteristics of system when β＝1．5

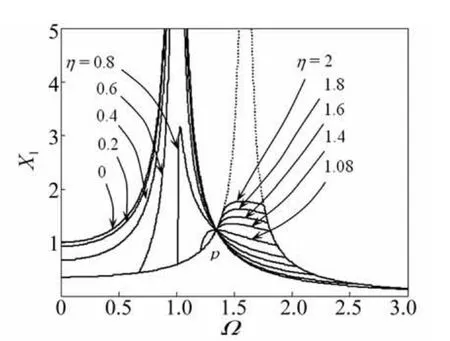
图5 刚度比β＝1．8时系统的幅频特性曲线（α＝0．1）Fig．5 Amplitude frequency characteristic curves of system when stiffness ratio β＝1．8 and α＝0．1

图6 刚度比β对系统幅频特性峰值的影响（α＝0．1）Fig．6 Influence of stiffness ratio β on the peak value of amplitude frequency characteristics of system when α＝0．1

图8 相对阻尼比γ对系统幅频特性的影响Fig．8 Influence of relative damping ratio γ on the amplitude frequency characteristics of system

如图7，增大阻尼比ζ1，ηopt值减小，图7（a）为ηopt＝0．93，图7（b）为ηopt＝0．81，同时系统实现完全耦合时所需的η值减小；当主系统含有粘性阻尼时，幅频特性曲线组成的曲线簇不再存在公共点，主系统的共振峰值得到有效控制，共振区变宽，且对最佳η值之前的幅频曲线影响较大，峰值下降明显，对最佳η值之后的幅频曲线影响微弱；随阻尼比ζ1的增大，控制参数η对系统减振过程的影响变弱。

图8表明，增大相对阻尼比γ，可以减小系统实现完全耦合时所需的η值，但是基本不影响系统未完全耦合前的幅频特性曲线，对最佳η值的影响也非常小，图8（a）为ηopt＝1．05，图8（b）为ηopt＝1．06。

3 智能弹簧减振系统参数的设计方法

根据上节的参数分析可知，无粘性阻尼的智能弹簧减振系统的幅频特性曲线汇交于公共点p，可根据公共点的性质，求得公共点p所对应的频率比Ωp为

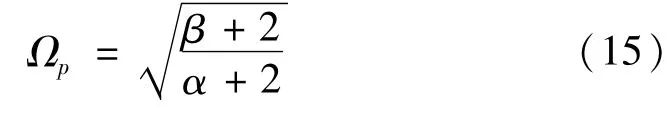
利用可导函数取极值的必要条件，再用式（15）确定的频率比Ωp替代其中的Ω，即可求出使幅频特性曲线的峰值正好位于p点时的最佳控制参数ηopt为

式（16）说明当α＞2时，会出现ηopt＜π／4的情况，使系统不能抑制主系统的共振。当Ω＝Ωp且η＝ηopt时，幅频特性曲线X1取得最小峰值，称其为最优峰值，即

式（15）～（17）的解析结果与上节通过数值分析计算出来的结果十分吻合，微小的误差来源于数值分析的计算精度和截断误差。因此，本节关于公共点的分析方法和结果是正确可靠的。

结合上节数值分析的结论与式（17）可知，当刚度比β的取值较大，且质量比α的取值偏离刚度比β越远时（要求α＜β）减振效果越好。根据上节的分析与式（15）可知，质量比α取小值时，耦合系统与主系统的固有频率相隔较远，公共频率比Ωp与二者之间的间隔较远，安全裕度高；但由式（16）可知，质量比α取大值时，最佳控制参数ηopt较小，说明所需压电陶瓷作动力较小，更易于实现。综合考虑，本文取0＜α＜1且β＞1，在满足系统要求和实际情况下，质量比α尽可能取大值。

对于无粘性阻尼的智能弹簧减振系统，由于0＜α ＜1，则0．91＜ηopt＜1．111。Ωp的取值要大于主系统的固有频率，同时要小于耦合系统的固有频率，所以有1当α＜1且β＞1时能满足此要求，说明本文取值的正确性。

进行智能弹簧减振系统参数设计时，应考虑PZTA控制电压的施加范围，一般应保证在PZTA产生最大作动力Nmax前，可实现智能弹簧装置的完全耦合［6］，即阻尼控制和刚度控制均可实现。式（15）～（17）中三个与公共点相关的信息是系统参数设计的重要依据。系统加入粘性阻尼后，虽然公共点不再存在，但幅频特性曲线仍在此点位置交错在一起，且阻尼的存在使系统完全耦合时所需的作动力N减小，阻尼比ζ1还能限制η ＜π／4时主系统的共振振幅。因此，可以先根据公共点的相关信息确定系统的质量比α和刚度比β，然后根据系统完全耦合的条件确定系统的阻尼比。根据常用的实际系统［20］，本文取阻尼比0．2。

图1所示智能弹簧减振系统中，振动结构的等效质量m1和允许的最大振幅X1，max为已知参数，外部激励F（t）的幅值f0和频率ω均可通过试验测定。智能弹簧减振系统参数设计可按照如下步骤进行：

（1）根据PZTA控制电压的施加范围，求出其产生的作动力范围，结合系统要求确定合适的η值作为最佳控制参数ηopt值，利用式（16）求得质量比α。

（2）根据系统工作转速区的安全裕度要求（一般偏离主系统固有频率20%以上），选择一个合适的最小频率比Ω（Ω＞1．2）值作为Ωp的初始值。

（3）利用式（15）可求出刚度比β的初始值。由定义Ω＝ω／ω1，求得ω1以及基本弹簧刚度k1的初始值，则有＝X1，maxk1／f0。若基本弹簧刚度k1（设定最小值）和刚度比β（设定最大值）在允许的取值范围内，进入第（4）步，否则取二者的最值，直接进入第（5）步。

（5）若从第（3）步进入此步，说明最大振幅要求可能尚未满足，首先取γ＝0，若能求出使系统满足最大振幅要求的阻尼比ζ1，进入下一步；若在ζ1的取值范围内无法找到合适的值，则取ζ1的最大值，并加入相对阻尼比γ，假定满足条件的相对阻尼比为γtest。若从第（4）步进入此步，说明满足最大振幅要求，在不考虑辅助系统的情况下，根据系统对自由振动的衰减速度要求选择合适的阻尼比ζ1。

（6）根据η＝μdN／f0，计算出PZTA控制电压最大时的控制参数ηmax值。在式（14）中，令η＝ηmax，并代入前面求得的α、β与ζ1值，即可确定相对阻尼比γ的取值范围。若γ在许可值范围内，根据实际情况选取（γ＞γtest），并进入下一步，否则返回第（1）步并增大ηopt值。

（7）系统加入阻尼后，ηopt及对应的最小振幅可能会减小，可通过计算确定其最终大小。利用质量比α的定义m2＝αm1，可求得主动弹簧质量m2。根据定义k2＝βk1，可求得主动弹簧刚度k2。根据定义c1＝2ζ1m1ω1，可求得c1。然后按照定义c2＝γc1，可求得c2。

本课题组与哈尔滨溶智纳芯科技有限公司合作开发的双向输出型压电陶瓷作动器，其控制电压范围为－20～150 V，单向最大输出力为500 N，双向输出力为1 000 N。根据文献［21］，将偏心量e减小一半，取如下已知设计参数：m1＝3．5 kg，ω＝471．24 rad／s，f0＝33．31 N，Nmax＝1 000 N，μd＝0．1，μs＝0．15。设计要求为：系统的最大振幅X1，max≤0．8×10－4m，k1＞1．5× 105N／m，β＜4。根据前面的分析可求得：α＝0．16，β＝2．66，ζ1＝0．11，γ≥1．12，Ωp＝1．47。图9为所设计系统的幅频特性曲线图（γ＝1．13），工作频率位置，系统量纲一最大振幅为0．829 8，对应原始坐标的振幅为0．77×10－4m；最佳控制参数为ηopt＝0．88，对应作动力为N＝293．13 N；当作动力N≥732．82 N时（η≥2．2），系统可实现完全耦合。因此，所选系统参数满足设计要求，从而确定系统的最终参数为：m2＝0．56 kg，k1＝3．6×105N／m，c1＝246．84 Ns／m，k2＝9．57×105N／m，c2＝278．93 Ns／m。

图9 系统幅频特性曲线图Fig．9 The amplitude frequency characteristics of system

4 结 论

本文研究了阻尼与刚度控制下智能弹簧减振系统的频响特性，分析了系统参数对系统幅频特性的影响。根据分析结论发现进行智能弹簧减振系统参数设计时，可以先利用无阻尼系统幅频特性曲线簇的公共点求得系统的刚度和质量，然后根据系统要求选择合适的基本弹簧阻尼，最后利用系统实现完全耦合的条件确定主动弹簧的阻尼大小，从而使系统能实现阻尼和刚度两种控制方式。

［1］Zou L H，Dai S L，John B W，et al．Grey forecasting model for active vibration control systems［J］．Journal of Sound and Vibration，2009，322（4－5）：690－706．

［2］张涛，黄宏彪，王斌，等．主动隔振作动器刚度放大与控制误差分析［J］．振动与冲击，2010，29（5）：50－53．

ZHANG Tao，HUANG Hong-biao，WANG Bin，et al．Stiffness amplification of actuator and governing error analysis in active vibration isolation［J］．Journal of Vibration and Shock，2010，29（5）：50－53．

［3］Gu H C，Song G B．Active vibration suppression of a flexible beam with piezoceramic patches using robust model reference control［J］．Smart Materials and Structures，2007，16（4）：1453－1459．

［4］Qiu Z C，Han J D，Zhang X M，et al．Active vibration control of a flexible beam using a non-collocated acceleration sensor and piezoelectric patch actuator［J］．Journal of Sound and Vibration，2009，326（3－5）：438－455．

［5］Shin C，Hong C，Jeong W B．Active vibration control of beam structuresusingaccelerationfeedbackcontrolwith piezoceramic actuators［J］．Journal of Sound and Vibration，2012，331（6）：1257－1269．

［6］Wickramasinghe V K，Chen Y，Zimcik D G，et al．Smart spring：a novel adaptive impedance control approach for active vibration suppression applications［J］．Proceedings of the SPIE-The International Society for Optical Engineering，2004，5390（1）：359－369．

［7］Chen Y，Zimcik D G，Wickramasinghe V K，et al．Research of an active tunable vibration absorber for helicopter vibration control［J］．Chinese Journal of Aeronautics，2003，16（4）：203－211．

［8］Chen Y，Wickramasinghe V K，Zimcik D G．Smart spring impedance control algorithm for helicopter blade harmonic vibration suppression［J］．Journal of Vibration and Control，2005，11（4）：543－560．

［9］Wickramasinghe V K，Chen Y，Zimzik D G．Experimental evaluation of the smart spring impedance control approach for adaptive vibration suppression［J］．Journal of Intelligent Material Systems and Structures，2008，19（2）：171－179．

［10］Nitzsche F，HaroldT，WickramasingheVK，etal．Development of a maximum energy extraction control for the Smart Spring［J］．Journal of Intelligent Material Systems and Structures，2005，16（11－12）：1057－1066．

［11］Afagh F F，Nitzsche F，Morozova N．Dynamic modelling and stability of hingeless helicopter blades with a smart spring ［J］．Aeronautical Journal，2004，108（1085）：369－378．

［12］Coppotelli G，Marzocca P，Ulker F D，et al．Experimental investigation on modal signature of smart spring／helicopter blade system［J］．Journal of Aircraft，2008，45（4）：1373－1380．

［13］Cavalini A A，Galavotti T V，Morais T S，et al．Vibration attenuation in rotating machines using smart spring mechanism ［J］．Mathematical Problems in Engineering，2011，2011：1 －14．［14］范天宇．弹性支承干摩擦阻尼器减振研究［D］．西安：西北工业大学，2006．

［15］王四季，廖明夫．主动式弹支干摩擦阻尼器控制转子振动的实验［J］．航空动力学报，2007，22（11）：1893 －1897．

WANG Si-ji，LIAO Ming-fu．Experimental investigation on rotor vibration control by elastic support／dry friction damper ［J］．Journal of Aerospace Power，2007，22（11）：1893 －1897．

［16］王四季，廖明夫．带弹支干摩擦阻尼器的转子振动控制策略和方法［J］．航空动力学报，2011，26（10）：2214 －2219．

WANG Si-ji，LIAO Min-fu．Control strategy and methods of rotor systems by an elastic support／dry friction damper［J］．Journal of Aerospace Power，2011，26（10）：2214－2219．

［17］Ni D，Zhu R P，Bao H Y，et al．Influence of damping ratios on the dynamical characteristics of vibration isolation system based on smart spring mechanism［A］．2012 3rd International Conference on System Science，Engineering Design and Manufacturing Informatization［C］．Chengdu：IEEE，2013：208－212．

［18］Di Bernardo M，Kowalczyk P，Nordmark A．Bifurcations of dynamical systems with sliding：derivation of normal form mapping［J］．Phys D，2002，170（3－4）：175－205．

［19］杨绍普，郭树起．一类摩擦振子的纯滑动运动分析［J］．振动与冲击，2009，28（10）：44－48．

YANG Shao-pu，GUO Shu-qi．Analysis of pure slip motions of a class of friction oscillator［J］．Journal of Vibration and Shock，2009，28（10）：44－48．

［20］Rao S S．Mechanical Vibrations［M］．Fourth Edition．New Jersey：Pearson Education Inc，2004：249－253．

［21］倪德，朱如鹏．智能弹簧装置减振性能的影响因素分析［J］．振动与冲击，2012，31（23）：87－91．

NI De，ZHU Ru-peng．Influencing factors of vibration suppression performance for a smart spring device［J］．Journal of Vibration and Shock，2012，31（23）：87－91．

A parametric design method for a smart damped spring vibration reduction system

NI De，ZHU Ru-peng，LU Feng-xia，FU Qiu-ju，BAO He-yun
（Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology，College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

A design method for system parameters of a smart spring system with linear viscous damping under harmonic excitation was presented，it could make the smart spring system implement both stiffness and damping control．Firstly，the analytical solutions to the frequency response characteristics of the smart spring system were deduced with the equivalent linearization method．Then，the influence of the system parameters on the amplitude frequency characteristics of the system was analyzed．The results showed that the amplitude frequency characteristic curve cluster has a common point for the smart spring system without viscous damping，but the common point disappears for the system with damping；the main parameters affecting the amplitude frequency characteristics of the system are mass ratio，stiffness ratio，damping ratio and control parameter；the system parameters affecting the magnitude of required actuator force to make two massspring systems become fully coupled are damping ratio and relative damping ratio．Based on the conclusions of the above parametric analysis，the selection scopes of the system parameters of the smart spring system were determined and the steps of parametric design were proposed．

parametric design；vibration suppression；smart spring；piezoceramics；dry friction；stiffness；damping

TH113．2；TH113．1

A

10．13465／j．cnki．jvs．2014．23．021

国家自然科学基金（51375226）；高等学校博士学科点专项科研基金资助课题（20113218110017）；江苏省高校优势学科建设工程资助；江苏省普通高校研究生科研创新计划资助项目（CXZZ11＿0199）；中央高校基本科研业务费专项资金资助

2013－07－02 修改稿收到日期：2013－12－04

倪德男，博士生，1986年11月生

朱如鹏男，博士，教授，1959年9月生