基于小波阈值的高速道岔振动信号降噪

周祥鑫，王小敏，杨 扬，郭 进，王 平

（1．西南交通大学信息科学与技术学院交通信息工程及控制省重点实验室，成都 610031；2．西南交通大学土木工程学院高速铁路线路工程教育部重点实验室，成都 610031）

基于小波阈值的高速道岔振动信号降噪

周祥鑫1，王小敏1，杨 扬1，郭 进1，王 平2

（1．西南交通大学信息科学与技术学院交通信息工程及控制省重点实验室，成都 610031；2．西南交通大学土木工程学院高速铁路线路工程教育部重点实验室，成都 610031）

在高速道岔伤损监测中，道岔振动信号是道岔伤损监测的重要信息来源，鉴于该信号在采集和传输过程中噪声干扰严重，影响伤损识别的准确性，研究了一种基于小波阈值的高速道岔振动信号降噪方法。详细讨论了道岔振动信号降噪过程中小波基、分解层数、阈值准则、阈值函数等参数的选择，并利用频响函数、主元分析和平均马氏距离分析降噪处理对伤损识别的影响。实验结果表明，该方法能有效降低噪声对伤损识别的干扰，为进一步对道岔进行伤损分析创造了良好的条件。

高速道岔；振动信号；小波阈值；降噪；伤损识别

高速道岔是高速铁路的基础设备，属于铁路线路中的活动部件和脆弱环节。在轮轨相互作用、外部载荷、环境和灾害等因素作用下，道岔易产生水平弯曲、拱腰、剥落掉块、裂纹甚至断裂等损伤，结构性能下降，严重影响道岔的使用安全。因此，实时掌握道岔的工作状态，是保障高速铁路行车安全和行车效率的关键。

基于结构频响函数（FRF）指标的伤损监测是研究高速道岔结构状态的主要手段之一［1］并在故障诊断领域得到广泛应用［2－4］，主要因为：①频响函数反映结构固有特性，与外界载荷无关，比时域信号稳定；②结构模态信息丰富，可完备表征结构的动力特性，既可反映结构整体特性，又可反映结构局部信息。环境随机激振下频响函数的估计［5］：

式中，Gyf（ω）表示输出信号与输入信号的互功率谱，Gff（ω）表示输入信号的自功率谱。由式（1）可知，道岔结构频响函数估计的准确性主要取决于对自谱和互谱的估计精度，很大程度上取决于实测信号的信噪比。而实测信号由不同动量的列车过岔激励产生，且受道岔活动部件相互作用影响，其激励和外部环境干扰复杂，导致道岔振动信号信噪比低，严重影响对频响函数的准确估计，最终影响伤损识别的准确率。因此，在伤损识别之前，对道岔振动信号进行降噪处理具有重要意义。

目前，针对机械设备振动信号，根据噪声产生机理和类型，常用的信号降噪方法有EMD降噪［6－7］、盲源分离［8］、小波阈值降噪［9－12］等。EMD方法对信号分解时无需进行参数设置，是一种自适应信号分解方法，但存在端点效应、模态混叠和实时性较差等不足，虽然Wu等［13］提出的集总平均经验模态分解（EEMD）算法有效解决了模态混叠问题，却导致计算量增加了1～2个数量级，不利于实时处理；盲源分离技术从混合信号中恢复源信号具有明显的效果，所需先验知识较少，但考虑道岔监测系统的成本因素，传感器安装数量有严格限制，而在欠定条件下准确提取源信号具有一定的困难。小波分析相对于Fourier分析，具有更好的时域分辨率和频域分辨率，被广泛应用于各类结构振动信号处理领域。文献［9］针对铁路机车振动信号，采用小波变换对其进行降噪处理，并取得明显的效果；文献［10－12］分别提出针对齿轮、发动机、轴承等旋转机械振动信号的小波阈值降噪方法。但对不同振动对象、不同激励和不同环境干扰下的实测信号进行小波降噪时，在小波参数的选取上缺乏理论指导，表现在小波基、分解层数、阈值等参数选取上存在很大的不确定性，甚至不同小波参数可能产生相反的去噪效果。

针对高速道岔伤损监测对信号降噪的有效性和实时性要求，本文提出一种基于小波参数优选的振动信号阈值降噪算法。通过构建与实测振动信号匹配的仿真信号，完成对小波基、分解层数、阈值等参数的优选，然后基于小波阈值去噪理论，确定优选降噪方案。在此基础上，结合实测列车激励道岔振动信号和试验平台道岔振动信号，分析了优选降噪方案对道岔伤损识别的影响。实验表明，本文方法对噪声的抑制有显著效果，并且满足在线监测的实时性要求；经降噪后的道岔振动信号有利于提高道岔伤损识别的准确性。

1 道岔振动信号的小波阈值降噪方案

1.1 小波阈值降噪的基本原理

由Donoho等［14］提出小波阈值降噪理论，其主要理论依据是：信号经小波分解后，有用成分的小波系数绝对值较大，而噪声成分的小波系数绝对值较小，通过设定阈值，将小于阈值的小波系数置零来达到滤除噪声的目的。

利用小于阈值降噪理论对一维信号降噪的具体步骤为：

（1）信号的小波分解：确定一个小波基和适当的分解层数，将信号分解得到相应的小波系数；

（2）小波系数阈值量化：对分解各层设定一个合适的阈值，将绝对值小于该阈值的小波系数置零，将绝对值大于该阈值的小波系数保留或作收缩处理；

（3）信号重建：将量化后的小波系数通过小波逆变换重建信号。

1.2 构建道岔振动仿真信号

在工程应用中，实测信号所含噪声未知，不利于对降噪参数的选择和降噪效果做出客观评价。因此，本文首先通过构建与实测振动信号匹配的仿真信号来确定优选降噪方案。图1（a）为实测列车激励的道岔振动信号，虚线域①所示信号为车轮刚好经过测点时的振动信号，将此类信号称为有效振动信号，将虚线域②所示信号称为间隙信号。

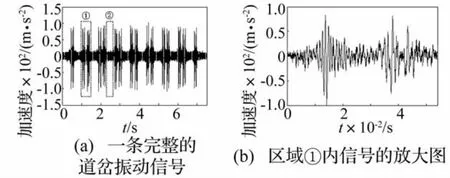
图1 实测列车激励的道岔振动信号Fig．1 Turnout vibration signal impelled by train

部分区域①信号放大如图1（b）所示，图示信号具有一定正弦特性，近似图2所示的拍波信号［15］，其产生函数为：

式中，A为信号的最大幅值，w1为共振频率，w2为包络的正弦波频率。w1与w2满足关系w2＝w1／2n，n为一个拍波的共振次数，将w2＝w1／2n代入（2）式得：

对式（3）乘以一个包络调节因子cos（kw1／2n）得到仿真信号：

式中，k为调节波形包络形状的系数，取k＝1．2。从图1（b）知实测道岔振动信号最大幅值A约为90，n约为24，经计算w1＝2 048 π，产生的道岔振动仿真信号如图3所示。由图可知，仿真信号与实测振动信号具有较好地相似性。

图2 拍波信号Fig．2 Beat wave signal

图3 仿真信号Fig．3 Simulation signal

1.3 选取小波阈值降噪参数

小波基类型的选取是影响降噪效果的重要因素，同一类型的小波基，其消失矩的选取也至关重要。通常在选取小波基时，小波形状与信号形状的相似度越高降噪效果越好［16］。经实验得到Daubechies小波、Symmlet小波和Coiflet小波通过调整消失矩能够与实测信号达到较高的相似度。

阈值的选取是影响降噪效果的另一个重要因素，如果阈值选择过大，信号中的部分有用信号将会被视为噪声滤除，导致重构信号存在严重失真；相反，如果阈值选择过小，信号的降噪效果不理想。其中阈值的确定与阈值准则息息相关，通常有四种小波阈值准则［17－19］：固定阈值（sqtwolog）、自适应阈值（rigrsure）、启发式阈值（heursure）、极大极小阈值（minimaxi）。最后，对小波系数的量化方法有软阈值法和硬阈值法［9］。

表1为小波阈值降噪各项参数，本文对22种小波，4种阈值准则和2种阈值函数进行对比分析，对信号分别进行2～10层分解，因此，上述小波参数的组合方式共有22×4×2×9＝1 584种。

表1 小波阈值降噪各项参数Tab.1 Parameters of wavelet threshold denoising.

1.4 确定降噪的优选方案

工程应用中，由于道岔安装环境、传感器安装位置、激励条件等因素的差异，导致实测道岔振动信号所含噪声强度不同，故降噪优选方案应具备较好的抗噪干扰能力。因此，本文对仿真信号分别添加－10 dB、0 dB、10 dB的高斯白噪声，分别进行降噪，并对降噪结果进行综合分析来确定优选方案。具体实验步骤为：

（1）确定阈值估计准则：对信号分别采用上述三类小波基进行10层分解，对分解的小波系数分别采用上述四类阈值准则计算阈值，并用软阈值函数对小波系数进行量化；

（2）确定阈值函数：对信号分别采用上述三类小波基进行10层分解，对分解的小波系数采用步骤（1）确定的阈值准则计算阈值，分别采用软阈值函数和硬阈值函数对小波系数进行量化；

（3）确定小波基和分解层数：根据步骤（1）和步骤（2），选取降噪效果较好且相当的几种小波基，并用这几种小波基分别对信号进行2～10层分解，对分解的小波系数采用步骤（1）、（2）确定的阈值准则和阈值量化方法进行阈值估计和系数量化。

对上述各步骤量化后的小波系数进行重构得降噪信号，并计算降噪信号的信噪比。由于加入的白噪声具有随机性，上述三个步骤的信噪比计算均采用100次降噪的信噪比统计平均值，分别对应图4～6。由图4可知，在不同噪声强度下，启发式阈值准则降噪效果均优于另外三种阈值准则。由图5可知，在不同噪声强度下，经软阈值函数量化后重构信号的信噪比均高于硬阈值函数的处理，且当携噪信号信噪比较低时，软阈值函数相对于硬阈值的优势表现得更为明显。

图4 不同阈值准则对应的信噪比（横坐标：＃1—db2，＃11—sym4，＃18—coif1）Fig．4 SNR of different threshold criteria

图5 软硬阈值对应的信噪比（横坐标：＃1—db2，＃11—sym4，＃18—coif1）Fig．5 SNR of soft threshold and hard threshold

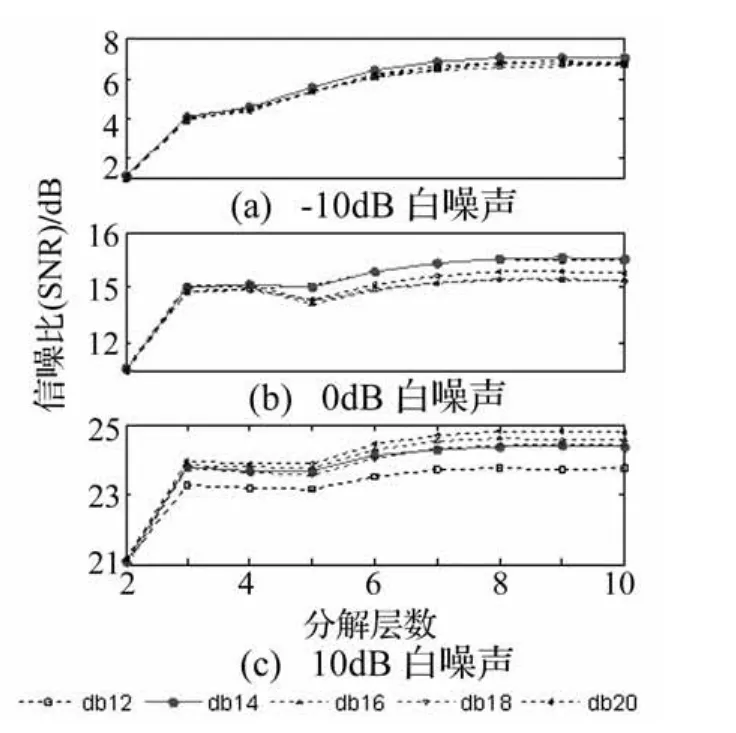
图6 不同分解层数对应的信噪比Fig．6 SNR of different decomposition scale

对比分析图4和图5可知，上述三类小波随着消失矩的增加，信噪比均呈上升趋势，但经db12、db14、db16、db18、db20处理后的信号信噪比相对更优，且信噪比非常接近。于是，图6在不同噪声强度下对这五种较优的小波作了进一步对比，即采用这五种小波基对信号均进行2～10层分解，并计算软阈值量化后重构信号的信噪比。由图可知，当信号信噪比较低时db14小波的降噪效果相对较优，当信号信噪比较高时，db20小波相对略优，但在工程应用中，实测道岔振动信号的信噪比通常较低，因此综合考虑宜选用db14小波。

据图6还可看出，信噪比随分解层数的增加而增大，但当分解层数达到7层时继续增加分解层数对信噪比的改善较小，因此宜对信号进行7层分解。

综上所述，针对道岔振动信号的降噪，本文确定优选降噪方案：采用db14小波，对信号进行7层分解，采用启发式阈值准则计算阈值，并用软阈值函数对各层小波系数进行量化。图7为优选方案对含0 dB白噪声的仿真信号的降噪效果，据图可知，在低信噪比的情况下，优选降噪方案仍能较准确重建原始干净信号，降噪后的信号失真较小。

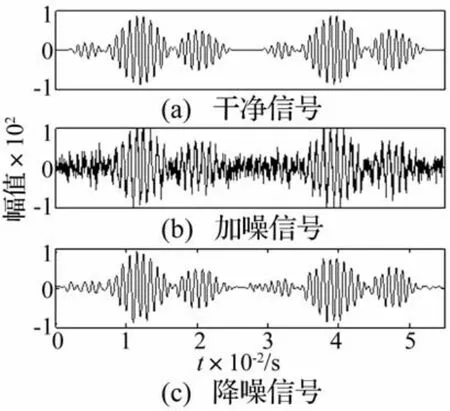
图7 仿真信号的降噪Fig．7 De-noising of simulation signal

2 实测信号降噪效果分析

分析两类实测道岔振动信号的降噪效果：

（1）实测列车激励道岔振动信号。该信号采集于成灌线犀浦站18号高速道岔，传感器在道岔上的安装位置如图8所示，每条曲尖轨安装14个传感器，传感器为MEAS传感器公司生产的8021－01加速度传感器。

图8 传感器的分布示意图Fig．8 The distribution diagram of the transducer

（2）高速道岔伤损监测试验平台的道岔振动信号。试验平台如图9（a）所示，道岔型号为18号道岔，激励源为一台安装在钢架小车上的离心振动机，其中一条曲尖轨无伤损，另一条曲尖轨尖端存在剥落掉块和裂纹伤损，如图9（b）所示。

图9 高速道岔伤损监测试验平台与伤损位置Fig．9 High-speed rail damage monitoring test platform and the position of damage

图10为对上述两类信号降噪的效果，由图10（a）可以看出，对于实测列车激励道岔振动信号的有效振动信号，降噪前信号的时域波形含有丰富的噪声毛刺，经降噪后能较好地消除噪声毛刺，信号的时域波形变得较为光滑，且降噪处理未对有用信号的能量造成衰减，同时从频谱也可以看出，对消除2．5 kHz以上的高频白噪声有明显的效果；对于间隙信号的降噪，如图10 （b），有用信号被强噪声淹没，通过降噪能有效提取出有用信号，高频噪声得到抑制；对图10（c）所示的试验平台有效振动信号，本文降噪方法对抑制其中的噪声同样具有明显效果。

3 优选降噪方案对伤损识别的影响

3.1 道岔的伤损识别策略

道岔振动信号的降噪，最终目的是为伤损识别提供高质量的数据，降噪效果的好坏直接影响伤损识别的结果。因此，本文将经优选方案降噪后的道岔振动信号和未经降噪的道岔振动信号分别进行伤损识别，并进行对比分析。根据文献［2－4］提出的基于频响函数伤损识别方法，高速道岔的伤损识别可以总结为如下步骤：

（1）构造频响矩阵：从采集的道岔振动信号中确定其中一个测点的信号作为虚拟激励，分别计算其他各测点处的频响函数，构成频响矩阵；

（2）数据降维：对频响矩阵进行主元分析，提取前m阶主元形成主元矩阵；

（3）计算伤损距离：计算道岔在无伤损状态下的参考主元矩阵与待伤损识别主元矩阵间的平均马氏距离：

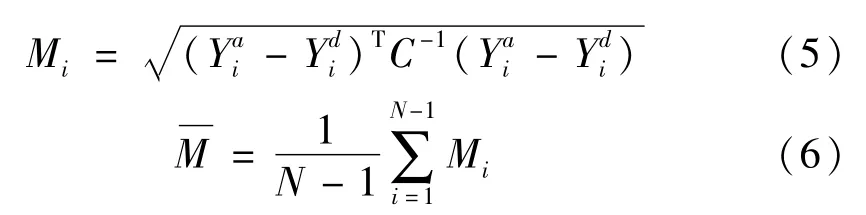
式中，Mi为对应测点间的马氏距离，i＝1，2，…，N－1， N为测点个数，Ya和Yd分别为参考主元矩阵和待识别的主元矩阵，C－1为矩阵Ya的协差阵，为平均马氏距离。

3.2 结果分析

降噪对频响函数的影响：如图11为成灌线犀浦站第13号测点频响函数的幅频曲线，由图可知，由未经降噪的振动信号计算所得频响函数，在高频段易形成虚假谱峰，主因对频响函数进行估计时，自谱和互谱的计算会因高频白噪声的干扰而受到影响。因此，通过降噪处理消除高频虚假谱峰的干扰，有利于获得更加准确的频响函数。

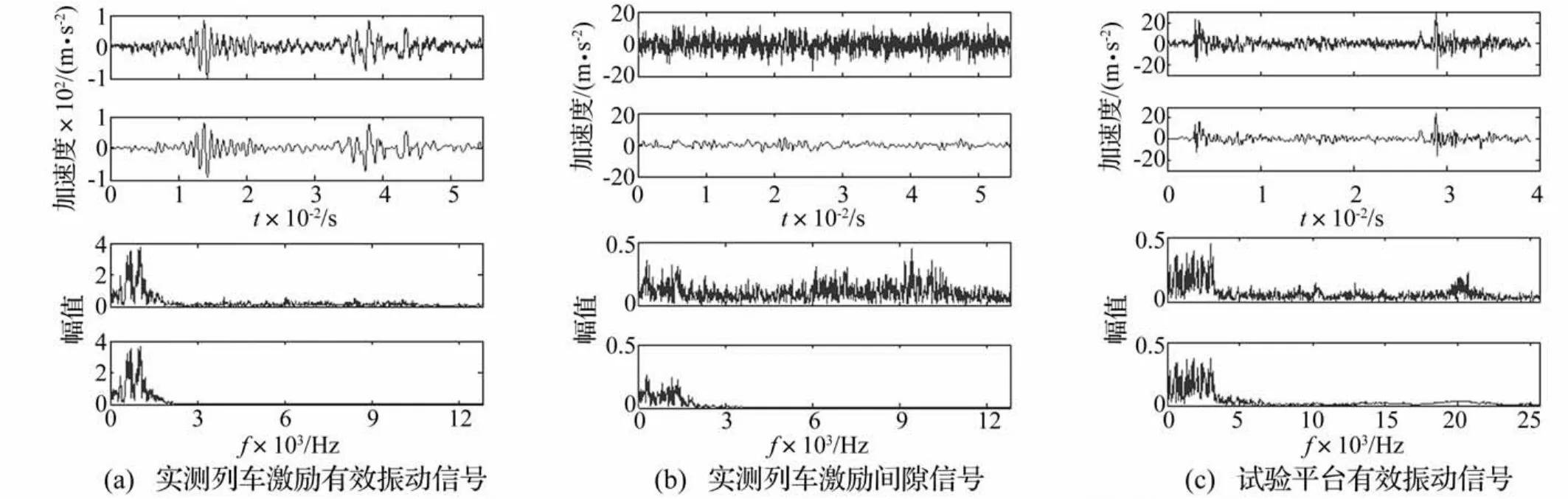
图10 本文优选方案的降噪效果Fig．10 De-noising effects of optimal scheme in this paper

表2 降噪前后前10阶特征值和累计贡献率Tab.2 The fisrt 10 eigenvalue and cumulative contribution rate

图11 第13号测点频响函数Fig．11 The FRF of 13thmeasure point

图12 实测列车激励道岔振动信号的平均马氏距离Fig．12 Average Mahalanobis distance of turnout vibration signal impelled by train

图13 试验平台道岔振动信号的平均马氏距离Fig．13 Average Mahalanobis distance of turnout vibration signal from test platform

降噪对数据降维的影响：利用主元分析对频响矩阵降维时，用前m阶主元矩阵取代高维频响矩阵，通常采用主元分析所得特征值的累计贡献率作为控制限。设控制限为95%，由表2可以看出，降噪前要达到95%的控制限，需前10阶主元，而降噪后前8阶主元即可达到要求，表明降噪处理使主元分析降维效果更好，降维后的主元矩阵所携带频响函数的主要信息更集中，即提高了数据压缩比。

降噪对伤损判别的影响：对降维后的主元矩阵采用（5）式和（6）式计算伤损前后的平均马氏距离。因为当道岔受到一定程度的损伤时，道岔的频响函数会发生一定变化，降维后的主元矩阵也会发生相应的变化，这种变化最终通过伤损前后主元矩阵的平均马氏距离量化，平均马氏距离越大，表明道岔整体伤损程度越大，反之则伤损程度越小。

文中选取15个批次的成灌线犀浦站无损伤道岔振动信号，任选其中一个批次的数据作为参考数据，对其他14批次数据进行伤损识别。如图12为成灌线犀浦站高速道岔伤损识别的平均马氏距离，由图可以看出，降噪之前第3和第10批次数据的平均马氏距离波动较大，如果伤损判决阈值设置不当，容易造成误判；通过降噪之后再进行伤损识别，使无伤损状态时平均马氏距离的值更集中，在一定程度上抑制噪声对伤损识别的干扰。

对高速道岔监测试验平台的振动信号，采集有伤损和无伤损两种工况下的数据各29个批次，将无伤损工况的一个批次数据作为参考数据。图13为降噪前后两种工况下的平均马氏距离，由图可知，降噪前两种工况的平均马氏距离的平均差值较小，某些批次数据的平均马氏距离存在重叠，不利于判决阈值的设置；经过降噪之后，两种工况的平均马氏距离间隔扩大，从而提高了两种工况的辨识度，可在一定程度上减小误判的概率。

4 结 论

本文针对道岔振动信号研究了一种基于小波阈值的降噪方法，对三类小波基、阈值准则、阈值函数、分解层数进行比较分析，确定一种参数优选降噪方案，并结合基于频响函数的伤损识别分析优选降噪方案对伤损识别的影响，结论如下：

（1）对道岔振动信号的小波阈值降噪，采用db14小波对信号进行7层分解、启发式阈值估计准则、软阈值量化函数的降噪方案，在滤除噪声的同时能较好地保留有用信号。与其他参数组合的降噪方案相比，优选方案具有更好的抗噪适应性。

（2）在伤损识别之前采用优选降噪方案对实测信号进行降噪，能更准确地估计频响函数、降低主元分析阶次与伤损识别计算量。道岔伤损识别结果表明：优选降噪方案能有效提高有损和无损工况间的辨识度，减小误判的概率，为进一步伤损位置定位、工况分类和定量分析提供了数据保障。

［1］王平．高速铁路道岔监测技术研究报告［R］．西南交通大学，2013．1．

［2］杨彦芳，宋玉普，纪卫红．基于实测频响函数主成分的在役网架损伤识别方法［J］．振动与冲击，2007，29（9）：55 －59．

YANGYan-fang，SONGYu-pu，JIWei-hong．An identification method of existing truss structural damage based on principal component analysis measured frequency response functions［J］．Journal of Vibration and Shock，2007，29 （9）：55－59．

［3］杨杰，李爱群，缪长青．大跨斜拉桥动力特性的主元特征提取［J］．东南大学学报：自然科学版，2006，36（4）：613 －616．

YANGJie，LIAi-qun，MIAOChang-qing．Principal component feature extraction of dynamic characters in long spancable-stayedbridge［J］．JournalofSoutheast University：Natural science，2006，36（4）：613－616．

［4］Lee U，ShinJ．Afrequencyresponsefunction-based structural damage identification method［J］．Computers and Structures，2002，80：117－132．

［5］李国强，李杰．工程结构动力检测理论与应用［M］．北京：科学出版社，2002，11－15．

［6］Meignen S，Oberlin T．A new algorithm for multicompon-ent signalsanalysisbasedonSsynchroSqueezing：withan application to signal sampling and denoising［J］．IEEE Transactions on Signal Processing，2012，60（11）：5787 －5798．

［7］Omitaomu O A，Protopopescu V A，Ganguly A R．Empirical modedecompositiontechniquewithconditionalmutual information for denoising operational sensor data［J］．IEEE Sensors Journal，2011，11（10）：2565－2575．

［8］Gelle G，Colas M，Serviere C．Blind source separation：A new pre-processing tool for rotating machines monitoring？［J］．IEEE Transactions on Instrumentation and Measurement，2003，52（3）：790－795．

［9］廖凯，张家栋．小波变换在机车振动信号分析中的应用研究［J］．铁道学报，2003，25（4）：115－118．

LIAO Kai，ZHANG Jia-dong．Application of wavelet transform in the vibrating signal analysis of locomotive bogie［J］．Journal of the China Railway Society，2003，25（4）：115 －118．

［10］Mohanty A R，Kar C．Fault detection in a multistage gearbox by demodulation of motor current waveform［J］．IEEE Transactions on Industrial Electronics，2006，53（4）：1258 －1296．

［11］臧玉萍，张德江．小波分层阈值降噪法及其在发动机振动信号分析中的应用［J］．振动与冲击，2009，28（8）：57 －60．

ZANG Yu-ping，ZHANG De-jiang．Per-level threshold denoising method using wavelet and its application in engine vi-bration analysis［J］．Journal of Vibration and Shock，2009，28（8）：57－60．

［12］Li Zhen，He Zheng-jia．Customized wavelet denoising using intra-and inter-scale dependency for bearing fault detection ［J］．Journal of Sound and Vibration，2008，313（1－2）：342－359．

［13］Wu Z，Huang N E．Ensemble empirical mode decomposition：a noise assisted data analysis method［J］．Advances in Adaptive Data Analysis，2009，1（1）：1－41．

［14］Donoho D L．De-noising by soft-thresholding［J］．IEEE Transactions on Information Theory，1995，41（3）：613 －627．

［15］王济，胡晓．MATLAB在振动信号处理中的应用［M］．北京：中国水利水电出版社，2006，147－149．

［16］Ma X，Zhou C，Kemp I J．Automated wavelet selection and thresholding for PD detection［J］．IEEE Electrical Insulation Magazine，2002，18（2）：37－45．

［17］Donoho D L，Johnstone I M，Adapting to unknown smoothness via wavelet shrinkage［J］．Journal of the American Statistical Association，1995，90（432）：1200－1224．

［18］Donoho D L，Johnstone I M，Minimax estimation via wavelet shrinkage［J］．Annals of Statistic，1998，26（3）：879－921．

［19］Donoho D L，Johnstone I M．Ideal spatial adaptation by avelet shrinkage［J］．Biometrika，1994，81（3）：425－455．

De-noising of high-speed turnout vibration signals based on wavelet threshold

ZHOU Xiang-xin1，WANG Xiao-min1，YANG Yang1，GUO Jin1，WANG Ping2
（1．Key Lab of Traffic Information Engineering and Control，Southwest Jiaotong University，Chengdu 610031，China；2．School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China）

Turnout vibration signals are an important information in high-speed turnout damage monitoring．As the signals are interfered by strong noise during the process of field acquisition and transmission，the accuracy of turnout damage identification based on its noisy vibration signals is declined seriously．To solve this problem，a denoising method is generally employed before turnout damage identification．The complex and noisy vibration samples from a site，however，raise the hurdle of denoising．Here，an effective denoising method based on wavelet threshold for turnout vibration signals was proposed．The selection of parameters，such as，wavelet basis，decomposition scale，threshold criteria and threshold function was empirically discussed for wavelet threshold denoising．Then，turnout damage identification analysis was conducted with the principal component analysis（PCA）of frequency response functions（FRF）and average Mahalanobis distance（MD）．The experimental results showed that the proposed method can be used to reduce the noise interference effectively for turnout damage identification，and create better conditions for further damage analysis．

high-speed turnout；vibration signal；wavelet threshold；de-noising；damage identification

TP274

A

10．13465／j．cnki．jvs．2014．23．036

铁道部科技研究开发计划重大项目（2011G009，2012X004－A，2013X012－A－1，2013X012－A－2）；四川省杰出青年培育基金（2011JQ0027）；中央高校基本科研业务费专项资金（SWJTU11CX041，SWJTU12CX099）

2013－08－01 修改稿收到日期：2013－12－19

周祥鑫男，硕士生，1988年生

王小敏男，博士，教授，1974年生