双重非对称转子支承系统实体有限元动力分析

马威猛，王建军

（北京航空航天大学能源与动力工程学院，北京 100191）

双重非对称转子支承系统实体有限元动力分析

马威猛，王建军

（北京航空航天大学能源与动力工程学院，北京 100191）

研究了同时考虑转子和支承非对称特征的转子支承系统3D有限元建模和振动特性分析方法。首先用ANSYS得到转子在旋转坐标系下的整体质量、刚度和科氏力矩阵；其次利用动静坐标变换关系得到旋转坐标系下的时变支承刚度；最后利用节点编号与矩阵行号的对应关系在整体矩阵中施加约束和时变支承刚度，得到系统的时变系数运动微分方程。基于弗洛凯理论和赫尔无穷行列式方法对方程求解得到系统的频率特性和稳定性。利用文献算例模型对该方法的有效性进行了验证，并对实际工程转子在考虑双重非对称特征时的振动特性进行了分析。

非对称；转子支承系统；3D有限元；时变系统；稳定性

转子支承系统是旋转机械的核心部件，其振动特性对旋转机械的工作性能和可靠性具有重要的影响。转子支承系统振动特性研究对旋转机械的结构设计、维修保养、振动控制、故障诊断等方面工作都具有重要的意义。

根据转子与支承的轴对称特征，转子支承系统可以分为：轴对称（axisymmetric）、支承非对称（anisotropic）、转子非对称（asymmetric）和双重非对称（anisotropic asymmetric）转子支承系统，其中双重非对称系统又称为一般（general）转子支承系统［1］。人们对轴对称转子支承系统开展了充分的研究工作，基于3D实体有限元的分析模型可以精确描述复杂截面转子的振动特性［2－4］。而在工程实际中，因加工、设计或故障破坏等原因，转子或支承部件通常会包含一些非对称特征，典型的如发电机转子、裂纹转子等。转静子上存在的非对称特征使得转子表现出独特的振动特性，需要进行专门的研究，如参数振动特性是双重非对称转子支承系统的主要特征［5］。

20世纪60年代以来，国外学者针对双重非对称转子支承系统的振动特性开展了广泛的定性［6－8］、定量研究［9－12］。在建模分析方法方面，Nandi［12－14］在不同的框架下提出并开展了基于3D实体有限元的非对称转子系统动力特性分析工作，Kim［15］仍在1D有限元的框架下考虑非对称转子支承系统的部件耦合问题。沈松等［16－19］在非对称转子系统的振动分析方面也做了出色的工作，但主要集中在非线性分析领域，对线性领域内双重非对称转子支承系统的建模和振动特性分析方法没有加以关注。

3D实体单元建模不需对转静子结构进行过多简化，可以真实反映转静子的结构特征，并且能够准确考虑转静子各部件之间的耦合效应，是转子动力学建模方法的发展趋势。目前，多数商用有限元分析软件已支持基于3D实体单元建模的转子动力学分析，但其分析功能仅能考虑轴对称或单一非对称转子支承系统，而不能进行双重非对称转子支承系统的振动特性计算。

本文利用商用有限元软件ANSYS的前处理功能，得到转子3D有限元模型的质量、刚度和科氏力矩阵，通过矩阵处理加入支承结构在旋转坐标描述下的时变刚度，得到转子支承系统的时变运动微分方程，然后基于时变系统分析的弗洛凯理论和无穷行列式方法将时变方程转化为一定截断阶次的时不变线性方程组，求解得到系统的频率特性和稳定性，实现双重非对称转子支承系统的3D有限元振动特性分析功能。文中首先介绍相关的分析理论，包括坐标系的选择，运动微分方程的建立以及基于弗洛凯理论的时变参数系统的求解方法；然后以两个算例对文中双重非对称转子振动特性分析方法的有效性和工程应用价值进行验证和说明。

1 坐标系选择

工程实际中，裂纹、键槽、非圆截面等非对称转子特征及各种形式的支承非对称特征可以抽象为图1所示的典型双重非对称转子支承系统［20］。图1中的非圆截面轴代表前述多种因素引起的转子刚度非对称特征，非圆截面盘代表转子的非对称转动惯量特征，正交方向上不同的支承刚度和阻尼则表示支承系统的非对称特征。

图1 双重非对称转子支承系统示意图Fig．1 Simple analysis model of anisotropic asymmetric rotor bearing system

对双重非对称转子支承系统而言，采用旋转或者固定坐标系描述系统运动不像单一非对称转子支承系统那样具有特殊的意义－选用合适的坐标系可以把时变微分方程转化为时不变微分方程的求解问题。双重非对称转子系统在固定或转动坐标系下描述均不能得到具有固定系数的运动微分方程。双重非对称转子支承系统在选取分析坐标系时，考虑到：①目前ANSYS等商用有限元分析软件仅支持非对称转子在旋转坐标系下的3D实体有限元分析；②若将静子系统的支承刚度以参数形式给出，在旋转坐标系下表达的时变刚度系数仅涉及支承点附近的几个相关自由度，表达形式简单。因此，一般选用随转子同速旋转的旋转坐标系对双重非对称转子支承系统的运动进行描述。

2 旋转坐标系下的运动微分方程

在旋转坐标系下，采用3D实体单元对非对称转子进行建模能够准确反映非对称几何特征或材料特征对转子截面弯曲刚度或转动惯量的影响。实体非对称转子在边界节点附近由刚度单元支承，刚度单元在各个支承方向的刚度差异反映支承系统的非对称特征。为方便描述，以下标nb标示转子的支承节点。在固定坐标系下，这些支点的刚度可以表示为［13］

转子支点在旋转坐标系下的支承刚度可由式（1）经坐标变换得到

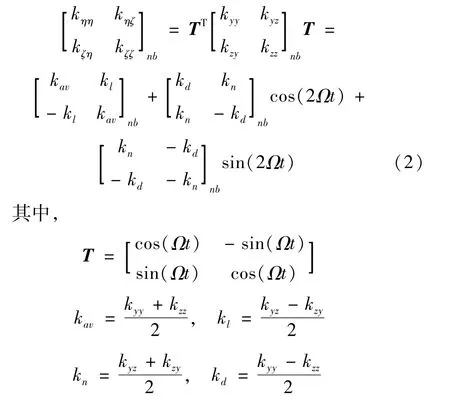
旋转坐标系下，无阻尼转子支承系统在外力作用下的运动微分方程可以写为

式中［Kr］是转子支承系统的刚度矩阵，由转子自身刚度和支承刚度组成，［Mr］是转子系统在旋转坐标系下的质量矩阵，［Cr］被称为科氏力矩阵，是反对称矩阵，｛U｝是转子系统在旋转坐标系下的位移向量，｛f｝则是在旋转坐标系下表示的外部载荷向量。

在ANSYS前处理模块中完成转子结构建模后，若不考虑支承的非对称特征，利用ANSYS的转子动力学分析模块可以直接得到方程（3）中各矩阵的元素数值；而考虑支承非对称时，刚度矩阵是时变的，需要进一步编程处理才能得到相应的矩阵。

考虑到支承刚度在旋转坐标系下的时变特征，方程（3）可以改写为

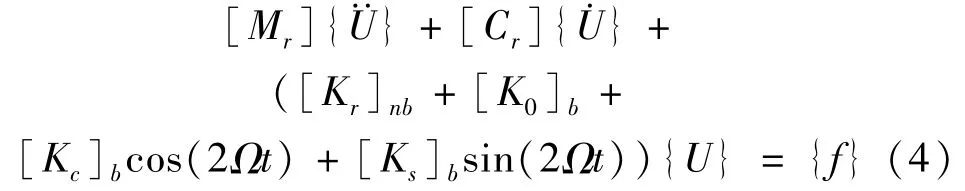
式中［Kr］nb是不考虑支承刚度时，转子系统在旋转坐标系下的刚度矩阵，可由ANSYS前处理模块直接得到；［K0］b是支承刚度的非时变项，而［Kc］b和［Ks］b则是支承刚度时变项中的余弦和正弦分量，支承刚度各矩阵由式（2）经坐标变换得到。

考虑到三角函数与复数的变换关系，方程（4）可写成复数形式，

3 时变参数系统的求解方法

时变参数系统的求解方法与一般时不变系统不同。弗洛凯理论和赫尔无穷行列式方法是分析时变参数系统常用的分析理论。

基于方程（5）的齐次方程，可对转子支承系统的自由振动特性进行分析。根据弗洛凯理论，假设方程解的形式为

其中，Λ是系统的基础特征频率，Φ是与Λ相对应的类模态矩阵。之所以称Φ为类模态，是因为其形式虽然与时不变系统的模态矩阵相似，但Φ具有时变的性质，其时变周期与运动微分方程中时变系统的周期一致。

其中，lj为Φ的第j阶阶次展开模态。

将式（6）和式（7）代入方程（5）的齐次方程中，并整理可以得到

方程（8）中，令指数项对应各阶次系数等于零可以得到

式（9）在截断阶次j＝∞时，与原时变微分方程是等价的，但在实际的计算中，需要进行适当阶次的截断，得到原时变微分方程解的近似值。求解得到各展开阶次的频率及特征向量后，根据式（7）可得到原时变微分运动方程的近似特征值Λ和类模态Φ。

式（9）可写成特征值求解问题的一般形式

上述特征值问题一般转换到状态空间进行求解。式（10）在状态空间中可以写为

在状态空间中求解式（11）的特征值问题，可得到相应的特征频率λ和特征向量Ψ，进而得到转子支承系统的近似特征频率Λ和特征向量Φ。

根据式（7）的阶次展开形式，可知每阶类模态Φp对应（2j＋1）个模态频率，考虑到双重非对称转子支承系统时变刚度的变化圆频率是2Ω，类模态Φp对应的模态频率中各阶次频率与基础频率的关系为

式中，ωj为第j阶阶次频率，ω0为基础频率，等于j＝0时的阶次频率。

根据式（12）对计算得到的特征频率按照基础频率分簇，并计算得到该基础频率簇对应的类模态。类模态各阶次频率的实部作为判断该阶类模态稳定性的依据。

4 算 例

这里用两个算例对文中分析方法的有效性及工程实际应用进行说明。

算例一中的分析模型来源于一篇参考文献［22］，文献作者基于1D有限元方法对模型的振动特性进行了分析。通过将本文基于3D有限元方法得到的结果与参考文献结果进行对比，对文中分析方法的有效性进行验证。

算例二的分析模型是某型航空发动机的低压转子。该转子由三级风扇、两级涡轮及连接轴组成，由三个支点进行支撑，支点刚度包含机匣刚度和轴承刚度。分析模型中考虑了中间支点机匣支承刚度在水平和竖直方向上的差异以及转子连接轴因装配误差引起的弯曲刚度差异。基于文中的分析方法，对上述非对称特征对转子振动特性的影响进行分析。

4.1 算例一

根据参考文献中提供的结构数据，建立的转子分析模型如图2所示。

图2 非对称转子的有限元模型Fig．2 Finite element model of asymmetric rotor

实体单元模型在支承结构处存在多个节点，不便于施加支承刚度约束，通常的做法是将支承位置的整圈实体单元节点刚化到圆心节点上，对圆心节点施加相应的约束［23］，文中沿用这种“刚化”处理方法。

利用商用有限元软件ANSYS的矩阵生成及组集功能，可以得到转子结构模型的质量、刚度和科氏力矩阵以及反映节点编号与矩阵行号对应关系的mapping文件。利用这些矩阵及对应关系，在MATLAB中对支承节点所对应的矩阵位置添加时变支承刚度，形成整个系统的时变运动微分方程。需要注意的是，在ANSYS中生成矩阵时，需要施加除径向支承刚度之外的其它约束条件，如轴向约束，转速等。

4．1．1 刚性支承下的结构验证

是基于1D框架给出的转子模型描述数据，如盘的极转动惯量、直径转动惯量等，而没有转子结构的3D几何信息。因此需对本文模型的结构特征进行验证。在转子两端支点处施加刚化约束，计算零转速下该非对称转子的模态频率，与文献算例模型在相同边界条件下的计算结果比较，可验证转子结构模型的正确性。本文模型与文献模型的零转速一阶弯曲模态频率列于表1中，两者误差较小，说明本文模型与文献模型具有一致的结构特征。

表1 本文与文献模型在零转速下的一阶弯曲频率Tab.1 First bending frequencies of the model for zero speed

4．1．2 弹性支承下的计算结果

在模型结构一致的基础上，考虑非对称支承刚度对转子振动特性的影响，分析该转子在旋转坐标系下的固有频率随转速变化的情况。

图3和图4分别给出了解的傅里叶展开指数为p＝0和p＝1时，转子在旋转坐标系下的频率转速变化曲线。

图3中，截断阶次p＝0，系统运动微分方程的等效线性方程组（9）仅包含A0项，不包含因支承刚度非对称引起的时变系数Δ项，此时求解得到的结果是转子在平均支承刚度下的基础振动频率w0。a0表示的是转子的一阶弯曲基础频率的正进动曲线。在转速范围820～950 r／min内，a0频率等于零，相应的特征根实部大于零，与参考文献中给出的转速不稳定区范围829～976 r／min一致。

图4中，截断阶次p＝1，计算得到的特征频率除包含基础振动频率w0外，还包含第一阶阶次振动频率w－1和w＋1。理论上，阶次频率与基础频率的相互关系由式（12）给出。图4中，a0，a＋1和a－1分别是实际计算得到的基础振动频率和＋1、－1阶阶次振动频率随转速的变化曲线。从图4中可以看出，a0曲线始终位于a＋1和a－1中间，并与它们的频率相差2Ω，与式（12）中给出的关系完全一致，并且，阶次频率变化曲线a＋1和a－1随着转速的变化发生耦合，产生新的转速不稳定区。上述结论与参考文献一致，通过对简单转子振动特性的分析，文中分析方法的有效性得到验证。

图3 p＝0时旋转坐标系下的频率转速图Fig．3 Evolution of frequencies in the rotating coordinate system for p＝0

图4 p＝1时旋转坐标系下的频率转速图Fig．4 Evolution of frequencies in the rotating coordinate system for p＝1

4.2 算例二

图5所示为某型航空发动机低压转子的三维有限元模型。模型通过改变连接轴的部分单元材料参数模拟转子在装配过程中可能产生的在正交方向上的弯曲刚度差异，材料参数改变区域在图5的局部放大图中以紫色标示。

图5 某型航空发动机转子有限元模型Fig．5 Finite element rotor model of an aero-engine

该转子采用1－1－1型支承方案，各支点位置如图5中标号1、2、3所示，其中2号支点在水平和竖直方向上具有不同的支承刚度，各支点的支承刚度列于表2中。

表2 某型发动机低压转子各支点支承刚度Tab.2 Bearing stiffnesses of the low pressure rotor of the aero-engine

采用文中的双重非对称转子支承系统振动特性分析方法，对该低压转子实体有限元模型在旋转坐标系下进行模态特性分析，得到转子模态频率随转速的变化曲线。

图6和图7分别是考虑方程解的傅里叶展开阶次p＝0和p＝1时的模态频率随转速的变化曲线。

图6中，截断阶次p＝0，得到非对称转子在对称支承刚度下的频率转速变化曲线。当各阶振型的正进动频率（图中a0，c0和e0）为0时，转子进入不稳定区。需要说明的是，在转速为0时，转子仅在第四阶振型上表现出明显的频率分离，前三阶振型在该转速下对转子连接轴段的局部弯曲刚度变化不敏感。

图6 p＝0时低压转子的频率转速变化曲线Fig．6 Evolution of nature frequencies of the low pressure rotor for p＝0

图7 p＝1时低压转子的频率转速变化曲线Fig．7 Evolution of nature frequencies of the low pressure rotor for p＝1

图7中，截断阶次p＝1，除得到转子的基础频率外，还得到转子振动类模态的一阶阶次频率。从图7中可以看出，考虑转子的一阶阶次频率后，转子的频率转速变换曲线变得更加复杂。图6中的每条基础频率w0，n曲线均扩展为w－1，n，w0，n，w＋1，n三条曲线，并且不是简单的扩展，从图7中可以看到，阶次频率与基础频率以及阶次频率之间出现多处的耦合和频率转向现象。阶次频率的耦合增加了转子的不稳定区范围。因此，与仅考虑单一非对称的转子不同，考虑转子的双重非对称特征时，转子的不稳定区区间增多，转子的安全工作转速范围变小。

另外需要说明的是，由于频率转向与阶次频率耦合，各阶频率与振型的对应关系非常复杂，并且分析人员更加关注的是不稳定区的范围，进行详细的振型区分也没有重要的意义，因此在图7中用相同的符号标示各阶频率变化曲线。

5 结 论

本文提出了基于3D实体有限单元建模的双重非对称转子支承系统的振动特性分析方法，详细给出了系统时变运动微分方程的组集推导过程以及频域特性的分析求解方法。文中以一个具有简单结构的双重非对称转子支承模型为例说明了方法的分析流程，对ANSYS模型分析矩阵的输出和MATLAB中支承刚度及约束施加的方法进行了必要的说明。对某型航空发动机低压转子的振动特性分析进一步说明的文中所提方法的工程实用价值。

参考文献

［1］Lee C W．Vibration analysis of rotors［M］．Dordrecht：Kluwer Academic Publishers，1993．

［2］Combescure D，Lazarus A．Refined finite element modelling forthevibrationanalysisoflargerotatingmachines：application to the gas turbine modular helium reactor power conversion unit［J］．Journal of Sound and Vibration，2008，318（4－5）：1262－1280．

［3］陈萌，洪杰，朱彬，等．基于实体单元的转子动力特性计算方法［J］．北京航空航天大学学报，2007，33（1）：10－13．

CHEN Meng，HONG Jie，ZHU Bin，et al．Rotor dynamic analysis based on solid element［J］．Journal of Beijing University of Aeronautics and Astronautics，2007，33（1）：10－13．

［4］Chatelet E，D'Ambrosio F，Jacquet-Richardet G．Toward global modelling approaches for dynamic analyses of rotating assemblies of turbomachines［J］．Journal of Sound and Vibration，2005，282（1－2）：163－178．

［5］Genta G．Dynamics of rotating systems［M］．springer，2005．

［6］Black H F．Parametrically excited lateral vibrations of an asymmetric slender shaft in asymmetrically flexible bearings ［J］．Journal of Mechanical Engineering Science，1969，11 （1）：57－67．

［7］Yamamoto T，Ota H，Kono K．On the unstable vibrations of a shaft with unsymmetrical stiffness carrying an unsymmetrical rotor［J］．Journal of Applied Mechanics，1968，35（2）：313 －321．

［8］Gladwell G M L，Stammers C W．On the stability of an unsymmetrical rigid rotor supported in unsymmetrical bearings ［J］．Journal of Sound and Vibration，1966，3：221－232．

［9］Genta G．Whirling of unsymmetrical rotors：a finite element approach based on complex coordinates［J］．Journal of Sound and Vibration，1988，124（1）：27－53．

［10］Lee C W，Suh J H，Hong S W．Modal analysis of rotor system using modulated co-ordinates for asymmetric rotor systemwithanisotropicstator［C］．8thInternational Conference on Vibrations in Rotating Machinery．University ofSwansea，UK：ProfessionalEngineeringPublishing （Institution of Mechanical Engineers），2004：575－584．

［11］Lee C W，Han D J，Hong S W．Modal analysis of periodically time-varying linear rotor systems using floquet theory［C］．Proceedings of the 7th IFToMM-Conference on Rotor Dynamics．Austria：International Conference on Rotor Dynamics，2006．

［12］Nandi A，Neogy S．An efficient scheme for stability analysis of finite element asymmetric rotor models in a rotating frame ［J］．Finite Elements in Analysis and Design，2005，41 （14）：1343－1364．

［13］Nandi A．Reduction of finite element equations for a rotor model on non-isotropic spring support in a rotating frame［J］．Finite Elements in Analysis and Design，2004，40（9）：935 －952．［14］Lazarus A，Prabel B，Combescure D．A 3d finite element model forthevibrationanalysisofasymmetricrotating machines［J］．Journal of Sound and Vibration，2010，329 （18）：3780－3797．

［15］Kim K T，Lee C W．Dynamic analysis of asymmetric bladedrotors supported by anisotropic stator［J］．Journal of Sound and Vibration，2012，331（24）：5224－5246．

［16］沈松，郑兆昌，应怀樵．非对称转子－轴承－基础系统的非线性振动［J］．振动与冲击，2004，23（4）：33－35．

SHENSong，ZHENGZhao-chang，YINGHuai-qiao．Nonlinear vibration of unsymmetrical rotor-bearing-foundation system［J］．Journal of Vibration and Shock，2004，23（4）：33－35．

［17］肖锡武，肖光华，杨叔子．不对称转子系统的参激强迫振动［J］．振动工程学报，2002（3）：71－74．

XIAO Xi-wu，XIAO Guang-hua，YANG Shu-zi．Parametrically excited and forced oscillations of an unsymmetrical rotor system［J］．Journal of Vibration Engineering，2002（3）：71－74．

［18］肖锡武，杨正茂，肖光华，等．不对称转子系统的非线性振动［J］．华中科技大学学报（自然科学版），2002（5）：81 －84．

XIAO Xi-wu，YANG Zheng-mao，XIAO Guang-hua，et al． Nonlinear oscillations of an unsymmetrical rotor system［J］．J．Huazhong Univ．of Sci．＆Tech．（Nature Science Edition），2002（5）：81－84．

［19］王培杰，滕弘飞，刘笃金，等．非对称复杂转子系统有限元动力分析［J］．固体力学学报，1991（4）：370－376．

WANG Pei-jie，TENG Hong-fei，LIU Du-jin，et al．The dynamic analysis for complex asymmetric rotor-bearing systems by finite element method［J］．Acta Mechanica Solida Sinica，1991（4）：370－376．

［20］Lee C W，Han D J，Suh J H，et al．Modal analysis of periodically time-varying linear rotor systems［J］．Journal of Sound and Vibration，2007，303（3－5）：553－574．

［21］Han D J．Modal analysis of periodically time-varying rotor systems using floquet theory and modulated coordinate transformation：applications to crack detection and modal balancing［D］．Daejeon：Korea Advanced Institute of Science and Technology，2006．

［22］Boru F E．Numerical and experimental response and stability investigations of anisotropic rotor-bearing systems［D］．Kassel：kassel university，2010．

［23］Rao J S，Sreenivas R．Dynamics of a three level rotor system using solid elements［C］．Proceedings of ASME Turbo Expo 2003．Atlanta，Georgia，USA：ASME，2003，601－606．

Dynamic analysis method of an anisotropic and asymmetric rotor-bearing system based on 3D FEM

MA Wei-meng，WANG Jian-jun
（School of Energy and Power Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

Dynamic analysis method of an anisotropic and asymmetric rotor-bearing system based on 3D finite element method was presented．The system mass，stiffness and Coriolis force matrices expressed with respect to a rotating coordinate system were generated with ANSYS．Time-varying bearing stiffness matrix with respect to the rotating coordinates was then obtained with a coordinate transformation．The differential equations of motion of the system were generated by applying constraints and time-varying bearing stiffness to the system matrices using the corresponding relationships between node number and row index of the matrices．Floquet theory and Hill infinite determinant method were adopted to solve the differential equations，frequency characteristics and stability of the system were obtained．The proposed method was validated based on a model in literature，and the proposed method was applied to analyze the dynamic behavior of an industrial rotor considering anisotropic and asymmetric characters．

asymmetric；rotor-bearing system；3D finite element；time-varying system；stability

V 231．96

A

10．13465／j．cnki．jvs．2014．23．002

2013－07－16 修改稿收到日期：2014－01－02

马威猛男，博士生，1987年1月生

王建军男，教授，博士生导师，1956年生