形状记忆合金对平板的刚度主动控制及优化布置研究
王明义,季宏丽,裘进浩,张 超
(南京航空航天大学机械结构力学及控制国家重点实验室,南京 210016)
形状记忆合金对平板的刚度主动控制及优化布置研究
王明义,季宏丽,裘进浩,张 超
(南京航空航天大学机械结构力学及控制国家重点实验室,南京 210016)
研究了基于形状记忆合金(Shape memory alloys,简称SMA)的平板结构刚度主动控制方法,提出了驱动器在平板上的布置形式。通过建立分析有限元模型并结合试验验证主动控制效果,结果表明利用形状记忆合金产生的回复应力可以显著地改变结构的刚度;通过调节形状记忆合金的驱动温度、含量和布置方式可以有效地控制结构刚度。在此基础上进一步采用遗传优化算法对驱动器布局方式进行优化,优化后的布置方案可实现利用较少的SMA驱动器提高刚度控制效果,为利用形状记忆合金实现对结构的刚度控制提供参考和借鉴。
形状记忆合金;刚度控制;回复应力;布局优化
伴随着航空航天、微电子机械等新技术的发展,系统的动力学特性成为各种系统设计的重要问题。模态特性作为结构的固有属性,关系着结构振动、噪声等相关的动力学问题,通过某些方法调节结构的刚度特性来避开结构共振频率是抑制共振的有效途径。随着智能材料的发展与应用,给实现对结构刚度控制带来了新方向。其中,形状记忆合金(Shape Memory Alloys,简称SMA)是一种特殊的合金材料,其主要的特性是形状记忆效应、超弹性效应和高阻尼效应[1-2]。由于在温度作用下,SMA材料可以发生相变和逆相变,两种晶相表现出不同的物理性质,将其融入到结构材料中或与结构构件相结合形成智能结构可以实现控制材料的形状、振动、屈曲等机械性能的目的[3-4]。
国内外对基于SMA的应用做了很多研究。Rogers等[5]最早提出把SMA纤维埋入复合材料结构中形成形状记忆合金纤维增强复合材料,可以通过对SMA的驱动实现对结构修改和控制。徐晓明等[6]利用瑞利-里兹方法计算和分析了SMA纤维复合材料变截面板簧在升温和降温过程中固有频率的变化规律,以及纤维铺层角度、含量和布置位置的影响。针对SMA的数值分析,Tawfik等[7]利用层合板理论建立SMA纤维复合材料模型,根据Hamilton原理和有限元法建立动力学控制方程。刘芹等[8]基于Liang-Rogers模型编写了ABAQUS中的相应UMAT用户材料子程序,模拟了形状记忆合金材料的超弹性行为和形状记忆效应。
以上结果主要从理论上对布置有SMA的复合材料结构进行计算和分析,但由于采用SMA纤维编织及制造复合材料技术尚未成熟[9]很难在实际工程中应用。本文提出了在平板结构上布置SMA丝驱动器的型式,实现了基于SMA丝驱动器对常规结构的刚度控制,同时进一步与优化算法结合对驱动器的布置位置进行设计,获得基于SMA的刚度主动控制策略。仿真过程中采用SMA一维Brinson本构模型引入“负热膨胀系数”模拟形状记忆效应建立有限元模型;通过对不同预应变的SMA回复应力进行测试,利用锤击模态试验获得SMA丝对平板的前3阶固有频率的改变率,研究了回复应力的大小与控制效果的关系,获得SMA的含量、驱动温度对结构控制的影响;最后利用遗传优化算法实现较高控制效果的驱动元件布置策略。这些结论对SMA智能结构设计和工程应用有一定参考价值。
1 基本理论和建模方法
1.1 SMA刚度控制原理
形状记忆合金对结构进行刚度控制主要利用其两个特性[10]:形状记忆效应和弹性模量随温度变化效应。形状记忆效应指的是把其拉伸至塑性变形,加热到其相变温度以上能恢复到原来形状。如果把其埋入结构中,由于两端被约束住,无法回到其原先的长度,将会产生很大的回复应力,利用这种回复应力作为驱动力可以实现对结构的控制,改变结构的内力分布和刚度特性。同时SMA本身的弹性模量在相变过程中也会发生很大变化,奥氏体状态下的弹性模量可达马氏体状态下的2倍~3倍。这两种SMA的特性形成了两种控制方式,称为主动应变能调整-Active Strain Energy Tuning(ASET)和主动性能调整-Active Property Tuning (APT)。
主动性能调整主要利用SMA的弹性模量变化特性,在实际控制结构中当SMA含量较少时控制效率不高,本文采用主动应变能调整来实现对结构的控制。SMA丝在驱动中产生回复力导致其处于受拉状态,力学模型可以看作两端固定的张紧弦,弦振动的i阶固有频率为:
从式(1)中可以看出,通过温度驱动SMA丝产生回复力F可以有效地提高丝的固有频率,当把SMA丝经过预拉伸后埋入结构中形成智能结构,未加热驱动时,整体结构自由振动有限元模态分析如下:
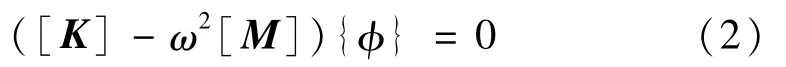
式中:[K]和[M]为结构的总体刚度矩阵和质量矩阵,ω为结构的固有频率。从可以看出,当质量不发生变化时,结构的模态频率只与其刚度有关。
当加热激活SMA丝时,SMA在结构中产生的回复应力直接影响平板的刚度,这种现象称为应力刚化。此时总体刚度矩阵可以表示为[K]=[KL]+[KSMA],[KL]为结构本身的刚度矩阵,[KSMA]为由SMA产生的回复应力作用引起的应力刚度矩阵,通过改变SMA产生的回复应力可以实现刚度控制来改变结构的固有频率,所以对回复应力与模态频率之间关系的研究是实现对结构刚度控制的关键。
1.2 SMA的一维本构模型
Brinson[11]通过热力学原理建立了SMA的一维本构方程:

式中,E、Ω、Θ分别为SMA的弹性模量、相变系数、热弹性模量;σ、ε、ξ和T表示应力、应变、马氏体含量和温度,下标0表示初始值。ξs为应力诱发的单晶马氏体,ξt为温度诱发的孪晶马氏体含量,有ξ=ξs+ξt。其中SMA的弹性模量和相变系数与马氏体含量有关,E和Ω可定义为:

式中,EA为100%奥氏体时的弹性模量,EM为100%马氏体时的弹性模量,εL为SMA最大可回复应变。
材料的应力不仅与应变有关,还与温度、马氏体含量有关。马氏体含量ξ决定SMA的相变过程,可以利用余弦马氏体相变动力学模型模拟马氏体含量与温度、应力之间的关系。
当温度大于奥氏体相变开始温度,相变由马氏体向奥氏体转变,

当温度小于马氏体相变开始温度,相变由奥氏体向马氏体转变

式中,AS和AF分别为SMA的奥氏体相变开始和结束温度;MS和MF分别为SMA的马氏体相变开始和结束温度;CA和CM分别为奥氏体和马氏体相变的应力与温度等效传热系数。由于应力作用会导致相变温度发生偏移,偏移后的温度记为和。当温度等于奥氏体相变开始温度,此时的马氏体含量为1,表明相变尚未开始;当温度大于奥氏体相变结束温度,此时的马氏体含量为0,表明相变结束。为确定和,可由式(4)导出:



1.3 有限元建模方法
采用温度驱动SMA丝,其材料参数与温度有关,利用在驱动过程中会产生的回复应力对结构进行控制,以往在有限元软件中直接通过力或位移边界条件定义,没有建立其与温度的耦合关系。SMA丝受热收缩产生的回复应力与普通材料受热膨胀产生的热应力相反,在实际仿真中可以等效为一个“负热膨胀系数”,由公式(8)给出了回复应力与等效热膨胀系数的关系,采用这个定义可以简化记忆合金丝本构在仿真中的运用难度,直接通过热膨胀系数建立其回复应力与温度之间的非线性关系,在仿真时可以通过施加温度边界条件,真实地反映其驱动特性。在有限元软件中定义材料“负热膨胀系数”αr进行等效,当没有初始应力和初始应变时,

图1是回复应力和等效热膨胀系数的计算流程,利用Brinson本构模型计算不同预应变的SMA丝弹性模量和回复应力与温度之间的关系。在建模中SMA丝采用梁单元和施加预应力进行仿真,可以模拟其弦振动问题,同时这也考虑了SMA丝在不同温度下的弹性模量变化对振动的影响。SMA丝驱动器的单元选为Bar元,通过对建立材料的“负热膨胀系数”可以模拟在升温中的收缩过程,即形状记忆效应。

图1 回复应力和等效热膨胀系数计算流程Fig.1 Recovery stress processing flow
在对结构建模时,考虑到SMA丝与铝板之间的连接用螺栓连接,在有限元模型中采用刚性连接RBAR单元来模拟。SMA回复应力对结构刚度的影响转化为预应力对模态的影响,使用有限元软件Nastran进行预应力模态分析(Preload for Modal analysis)。
2 实验平台搭建
2.1 实验模型结构
实验模型主要由SMA丝和铝板组成。SMA丝在使用前需要预拉伸到一定长度,并以一定形式固定在铝板表面。实验过程中通过温度驱动SMA丝对结构进行控制。
本文采用直径为0.5 mm的Ni-Ti形状记忆合金丝作刚度控制的驱动器。SMA丝使用前需要经过预拉伸以满足其作为驱动器的使用要求,图2是SMA丝预拉伸和回复应力测试装置,主要由步进电机、滚珠丝杆滑台、步进电机控制器、拉力传感器、温度采集卡、恒流电源和上位机组成。通过上位机控制步进电机运转带动滑台对SMA丝进行预拉伸来制备预应变的试件;通过恒流源进行电流加热,温度采集卡和拉力传感器获得回复应力与温度之间的关系。

图2 SMA丝预拉伸、回复应力测试装置Fig.2 A device for SMA prestretching and recovery stress measurements

图3 螺栓连接示意图Fig.3 Schematic diagram of bolt-joint connector
形状记忆合金丝在铝板表面的布置形式主要考虑两方面:①由于加热驱动SMA丝时,能产生很大的回复应力,在与铝板的接触部位需要完全约束住;②由于加热形式采用电流加热,SMA丝不能与铝板直接接触。综合这两个因素,SMA丝通过螺栓连接在铝板表面,具体实验模型见图3。
2.2 实验平台构建
实验平台主要由实验模型四边固支框架、实验模型对象、信号调理仪、力锤、PXI数据采集机箱、温度传感器和恒流源组成,具体组成方式如图4。采用恒流源对SMA丝施加电流进行加热驱动,温度传感器读取不同电流下驱动器的作动温度,在不同温度下对结构进行锤击模态试验获取其各阶固有频率值。

图4 模态试验平台Fig.4 The modal experiment platform
3 结果讨论与分析
3.1 回复应力的测试
SMA的材料参数见下表,通过图2的装置对试样进行拉伸并进行回复应力的测试。图5给出了预应变为1%、1.8%、4%、5.2%、6%的试件回复应力与温度的关系曲线,并与利用Brinson一维本构的计算值进行对比。

表1 SMA材料参数Tab.1 SMA material properties

图5 SMA回复应力随温度变化曲线Fig.5 The variation of the recovery stress of SMAs with temperature
从图中可以发现,SMA在受限回复过程中由于回复应力的作用,其相变温度被延后,如6%预应变的SMA在完全相变时能产生520 MPa的回复应力,此时使其完全相变温度需要80℃。这是由于应力会导致马氏体相变,只有当克服应力与温度达到平衡点才会发生相变。从图中的各条曲线也可以看出,相变结束温度与预应变有关,初始预应变越大,产生回复应力越大,使得完全相变温度提高。试验值与理论有一定差距,这是因为在试验过程中采用热电偶采集温度,由于与SMA丝的接触面积很小、温度的传导很快,产生了一定误差。
3.2 刚度主动控制
在铝板上布置预应变为6%的SMA丝对其进行刚度控制,图6给出了布置4根SMA丝的铝板有限元模型,每根SMA丝通过5个螺栓连接在铝板上。SMA丝和铝板分别采用梁元和壳元进行模拟,螺栓连接采用刚性单元RBAR建模,对模型施加温度边界条件模拟驱动前后铝板固有频率变化,温度范围分别取28℃(相变前)、40℃、50℃、60℃、70℃、80℃(相变后),100℃,对实验模型通过改变施加在SMA丝上的电流调节温度,并进行锤击模态试验获得相应驱动温度下的固有频率。图7给出了不同温度下模态试验和有限元结果的一阶固有频率。

图6 有限元模型Fig.6 The finite element model
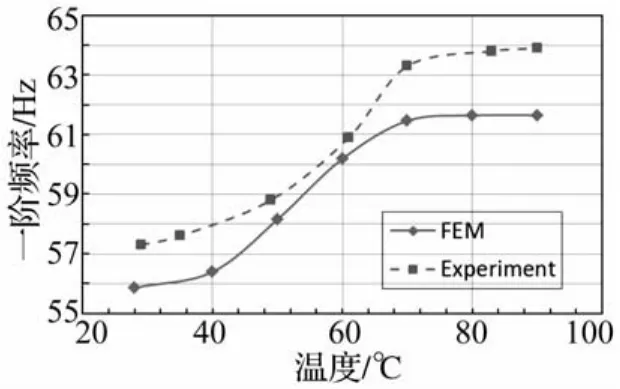
图7 结构一阶固有频率随温度变化曲线Fig.7 The variation of first natural frequency with temperature
图7中可以发现,有限元结果与实验结果符合的较好,利用Brinson一维本构,在仿真过程中通过“负热膨胀系数”引入SMA的形状记忆效应是切实可行的。通过驱动SMA可以控制结构刚度主要因为受限状态下的SMA产生回复应力改变了结构中的内力分布,发生应力刚化现象,结构在拉应力状态下提高结构刚度。为了进一步比较刚度控制效果,定义模态频率改变率η为:

式中,η为无量纲因子,反映了SMA丝驱动后产生应力刚化对模态频率的影响程度;fact为SMA驱动后结构的固有频率;fnon为未驱动SMA丝时结构的固有频率。图8是在不同温度下对上述布置4根SMA丝铝板一阶模态频率改变率的实验值与有限元结果对比图。可以发现,通过改变驱动温度能实现对结构刚度的主动控制;当到达SMA相变结束温度,此时回复应力最大,所达到的控制效果也越大。从图8与图5比较也可以发现,模态频率改变率与回复应力变化有相同的趋势关系,进一步验证了产生的回复应力是实现SMA对结构刚度控制的主要因素。
3.3 SMA布置方式对结构刚度的影响
考虑到SMA含量和布置方式对结构刚度的影响,本文针对上述结构分别均匀布置2根、4根和6根SMA丝在铝板上,每根SMA丝分别以5个螺栓连接在铝板上,布置方式见图9。表2给出了不同数量SMA丝对结构前三阶固有频率的控制效果。

图9 SMA在板上的三种布置方式Fig.9 The three configurations of SMA on the plate

表2 布置方式对控制效果的影响Tab.2 The control results under different configurations
从表2中可以看出,相对更容易发生的低阶固有振动,由于其所需破坏的能量较小,SMA对低阶频率具有更明显的调节作用;同时,可以发现通过改变SMA丝的含量和布置形式对结构的各阶频率具有不同的调节效果。这是由于SMA丝的布置方式和布置位置对各阶模态频率有不同程度的影响作用。从表2的结果中可以看出,布置有2根SMA丝的结构对1、2阶频率的控制效果较好,对第三阶基本没有控制效果;而布置有4根SMA丝的结构对2、3阶的控制效果较好,但对第1阶反而没布置有2根SMA丝的效果好;布置有6 根SMA丝的结构对前三阶都有较好的控制效果。对比图9和表2可以猜测,在各阶振型的峰值点布置SMA丝可以使得相应阶的固有频率取得较好的控制效果。
3.4 基于遗传算法的布置优化
前面的分析可以看出SMA对结构的刚度控制效果与其产生的回复应力、含量和布置位置有密切关系,而改变其在结构中布置位置往往最容易实现,本文以遗传算法为优化工具,以驱动器的布置位置为设计变量,分别以板的前三阶固有频率偏移量最大为适应度函数,将驱动器的位置坐标采用格雷码编码,利用遗传算法寻找全局最优布局,实现对板的最大刚度控制。遗传算法是模拟自然选择和生物进化过程的计算模型,通过模拟自然进化过程搜索最优解的方法。由于遗传算法从问题解的串集开始搜索,而不是从单个解开始,所以不容易误入局部最优解,特别适用于这种驱动器位置的随机布置优化。
本文的铝板结构上布置有4个SMA丝驱动器进行刚度控制,每个SMA丝两端通过2个螺栓连接在平板上,利用遗传算法对它们的坐标位置进行优化,以驱动前后最大频率偏移量为适应度函数,应用遗传算法进行驱动元件的布置位置进行优化时,优化参数选择如下:种群规模取为10,交叉概率取为0.6,变异概率取为0.01。通过有限元软件Nastran计算每次坐标更新后SMA驱动前后固有频率的改变量。对于每个驱动器确定其位置需要4个设计变量,设计变量的搜索范围为板的结构边界,即:

图10是针对前三阶固有频率最大偏移量的优化结果和相应的驱动器布置形式。不难看出,采用遗传算法针对本文的SMA驱动器布置位置优化取得较好的结果,搜索很快趋于收敛。从获得的最优布置形式可以发现,根据各阶频率控制的不同,驱动器的布置位置也有很大区别,当驱动器的一端都集中在模态振型峰值点附近,控制效果越明显,这与前面的结论相一致。表3给出了前三阶频率偏移量优化后的详细对比,由于SMA产生的驱动能量很大,经过优化后,采用少量SMA就能对结构进行有效控制,而对整体结构产生的重量影响很小。

图10 优化结果和布局Fig.10 Optimization results and layouts

表3 控制效果对比Tab.3 Control effect contrast
4 结 论
基于Brinson一维本构模型,引入“负热膨胀系数”模拟形状记忆效应,建立布置有SMA丝的平板有限元模型,通过回复应力和模态试验验证了有限元分析的正确性。结合有限元元仿真和模态试验研究了基于形状记忆合金的刚度主动控制,利用遗传算法对驱动器布置位置进行优化,得到形状记忆合金对平板结构刚度控制的一般策略。主要结论如下:
(1)结构的固有频率随SMA的驱动温度的变化而变化,可以通过调节SMA的驱动温度来实现对结构的刚度控制。
(2)预应变越大的SMA所能产生的回复应力也越大。回复应力是结构刚度控制的主要因素,回复应力越大所能产生的控制效果也越大。
(3)SMA丝在铝板上的布置位置对结构刚度控制有很大影响。通过改变布置位置可以改善对不同阶模态频率的控制效果,在各阶振型峰值点布置SMA丝可以使得相应阶的固有频率取得最好的控制效果。
(4)采用遗传算法可以解决针对SMA驱动器的布局优化问题,经过优化后可以实现较少的驱动器对结构较高的刚度控制效果。
[1]Ge S S,Tee K P,Vahhi I E,et al.Tracking and vibration control of flexible robots using shape memory alloys[J].Mechatronics,IEEE/ASME Transactions on,2006,11(6):690-698.
[2]朱晓锦,陆美玉,赵晓瑜,等.光纤机敏结构振动形态感知及其SMA致动控制[J].振动,测试与诊断,2008,28 (4):327-333.
ZHU Xiao-jing,LU Mei-yu,ZHAO Xiao-yu,et al.Vibration shape perception and SMA actuating control of fiber optic smart structure[J].Journal of Vibration,Measurement&Diagnosis,2008,28(4):327-333.
[3]王军,郦正能,叶宁.形状记忆合金智能结构的主动振动抑制研究[J].航空学报,2002,23(5):427-430.
WANG Jun,LI Zheng-neng,YE Ning.Research on active vibration suppression of smart structure embedded with shape memory alloy[J].Acta Aeronautica Et Astronautica Sinica,2002,23(5):427-430.
[4]He Y Y,Oi S,Chu F L,et al.Vibration control of a rotorbearing system using shape memory alloy:I.Theory[J].Smart materials and structures,2007,16(1):114.
[5]Rogers C A,Liang C,Jia J.Behavior of shape memory alloy reinforced composite plates,Part 1:model formulation and control concepts[C].Proceedings of the 30th Structures,Structural Dynamics and Materials Conference,1989:3-5.
[6]徐晓明,任勇生,杜向红.SMA纤维复合材料变截面板簧固有频率特性研究[J].振动与冲击,2012,31(14):164-170.
XU Xiao-ming,REN Yong-sheng,DU Xiang-hong.Natural frequency of variable cross-section leaf spring made of SMA fiber composite material[J].Journal of Vibration and Shock,2012,31(14):164-170.
[7]Tawfik M,Ro J J,Mei C.Thermal post-buckling and aeroelastic behavior of shape memory alloy reinforced plates [J].Smart Materials and Structures,2002,11(2):297.
[8]刘芹,任建亭,姜节胜.埋入SMA丝的复合材料层合板在热激励下的自由振动分析[J].振动与冲击,2008,27 (9):55-58.
LIU Qin,REN Jian-ting,JIANG Jie-sheng.Free vibration analysis of A composite laminated plate with embedded SMA wires under thermal excitation[J].Journal of Vibration and Shock,2008,27(9):55-58.
[9]Boussu F,Bailleul G,Petitniot J L,et al.Development of shape memory alloy fabrics for composite structures[J].Autex Res J,2002,2:1-7.
[10]韩玉林,李爱群,林萍华,等.基于形状记忆合金的结构振动控制研究与展望[J].东南大学学报(自然科学版),2000,30(1):146-154.
HAN Yu-lin,LI Ai-qun,LIN Ping-hua,et al.Research and prospect of civil structure vibration control by shape memory alloy[J].Journal of southeast university(Natural Science Edition),2000,30(1):146-154.
[11]Brinson L C.One-dimensional constitutive behavior of SMA:Thermomechanicalderivationwithnon-constantmaterial functions[J].Intelligent Material Systems and Structures,1993,4(2):229-242.
Plate stiffness active control with shape memory alloys and layout optimization
WANG Ming-yi,JI Hong-li,QIU Jin-hao,ZHANG Chao
(State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
The stiffness active control of a plate structure with shape memory alloys(SMA)was investigated and the layout optimization of actuators on the plate was presented.A FE model was established to analyze,together with some tests to validated by experimental results.The results indicated that the recovery stress produced by SMA is the main factor to change the structural stiffness.Meanwhile,it is effective to control the structure stiffness by adjusting temperature,volume and arrangement of SMA.Furthermore,the layout of SMA actuators was optimized by using a genetic algorithm.The results showed that the optimized layout is more effective with less SMA actuators.The results provide a reference for structure stiffness control.
shape memory alloys(SMA);stiffness control;recovery stress;layout optimization
TH135.2
A
10.13465/j.cnki.jvs.2014.23.006
国家自然科学基金资助项目(11372133,51375228);航空基金(20131552025);江南高校优秀学科建设工程项目;中国博士后基金(2014T70514)
2013-09-12 修改稿收到日期:2013-12-12
王明义男,硕士生,1989年8月生
季宏丽女,副教授,硕士生导师,1983年2月生

