玻璃对单层索网动力响应的影响
闫雁军,余志祥,李 晗,张其林
(1.同济大学土木学院建工系,上海 200092;2.上海建工七建集团有限公司 200050;3.西南交通大学土木学院建工系,成都 611756)
玻璃对单层索网动力响应的影响
闫雁军1,2,余志祥3,李 晗1,张其林1
(1.同济大学土木学院建工系,上海 200092;2.上海建工七建集团有限公司 200050;3.西南交通大学土木学院建工系,成都 611756)
为保证玻璃与与索网的协同变形,建立包含玻璃面板、索网、爪件、密封胶的有限元模型,真实反映了单层索网幕墙的传力途径;根据有限元模型,研究玻璃面板对单层索网静力性能和动力特性的影响;在此基础上,考虑索网幕墙周围建筑建立数值风洞,建立流固耦合模型,研究索网玻璃幕墙振动特性;以索网在平均风荷载作用下到达的新平衡位置为基准,采用频域方法计算单层索网风致动力响应。对比分析结果表明:风荷载作用下,索网幕墙主要做受迫振动,振动为窄带过程;玻璃面板有效降低了索网的平均位移和脉动响应。
玻璃面板;单层索网玻璃幕墙;流固耦合;频域法
单层索网点支承玻璃幕墙,体态轻盈、造型美观,在国内外得到广泛的应用。与其他结构形式的玻璃幕墙相比,单层索网点支承幕墙跨度大、刚度柔、几何非线性明显等特点使得结构对风荷载较为敏感,成为实际工程设计重点考虑的问题之一。冯若强等[1-7]对平面索网玻璃幕墙的静力性能进行了试验及数值模拟,研究表明,玻璃对结构的整体刚度有一定贡献,结构整体挠度与索直径和预张力也有一定关系,玻璃胶对降低索网挠度有一定贡献,对索网应力影响不大。考虑玻璃参与工作的单层索网玻璃幕墙自振特性研究表明[8-11]:安装玻璃后,由于结构质量比刚度增加更为显著,结构频率降低;玻璃的抗弯效应对结构第一阶模态影响较小,对结构的高阶模态影响明显;试验中未考虑玻璃胶,玻璃整体协同作用无法发挥,玻璃对刚度贡献减小。
另外,针对单层平面索网风致动力响应,既有研究多以结构在平均风荷载作用下的初始变形为平衡位置,忽略玻璃面板对结构刚度的影响,采用频域方法研究结构的风致响应[12-14]。频域法认为索网在初始变形后近似为线性结构,没考虑实际风致振动的非线性因素;同时该方法忽略了玻璃面板对结构的影响,结果存在一定的偏差。
本文考虑玻璃胶和爪件,建立了玻璃和索网协同工作的有限元模型,对点支承索网玻璃幕墙的变形和动力特性进行分析。根据幕墙周围建筑,建立数值风洞模型,采用流固耦合方法对单层索网玻璃幕墙进行风致动力响应分析,与频域法对单层索网的分析结果相比较,研究了玻璃面板对单层索网动力响应的影响。
1 流固耦合理论
1.1 流固耦合方程
流固耦合(Fluid Structure Interface,FSI)一个重要特征是流体与固体两相介质的相互作用,固体在流体作用下发生变形、运动;固体变形或运动反过来又影响流体流动,从而改变流体载荷的分布和大小。介质不同、耦合机理不同,产生了多种流固耦合现象。流固耦合整体方程为:

式中ρ,p,uf分别代表了流体密度、压力和速度,Mf、fρ、fp、fu分别代表流体质量矩阵、密度常数、压力向量和速度向量。将界面上的固体自由度表示为sf,界面上的流体自由度表示为fs,L代表荷载矩阵,σsf代表界面上的流体荷载。

1.2 流固耦合计算方法
对流固耦合方程进行求解时,有两种算法。直接耦合算法(Direct Coupling Method)将结构、流场、耦合界面的物理量统一在一个方程组进行直接求解。该方法适用性宽泛,但由于计算量庞大,发展比较缓慢。迭代耦合算法(Iterative Coupling Method)又称分离式算法(Partitioned Method),其基本思想是流场、结构在各自的CFD和CSD程序中完成计算,通过流固耦合界面完成双向数据传递、交替更新,一般按照“流体⇆耦合边界⇆结构”双向循环迭代求解(图1)直至达到收敛。本文采用迭代耦合算法,下边简要介绍一下计算步骤:



图1 双向耦合求解策略Fig.1 FSI solution method
(5)核实应力和位移的残差是否满足要求。如果不满足要求,则返回第一步,继续迭代求解变量,直到收敛。迭代步如果超出设定的上限值,程序会自动终止并提示不收敛。
双向迭代算法思路清晰,可以依托现有的CFD和CSD软件,理论难度大大降低,仅需要提高流固耦合界面上数值跟踪精度即可获得较为理想的解。
1.3 收敛判断准则
由于流体方程是非线性的,流固耦合方程也具有非线性特性。求解方程的过程实质上是一个反复迭代逼近真实解的过程。在迭代过程中,需要设立应力(公式(5))或位移(公式(6))准则来判断是否收敛。

式中ετ和εd分别是应力和位移收敛容差,ε0为预先设定的常数(≡10-8)防止应力或者位移太小。
1.4 FSI边界网格及节点插值
当FSI边界为非同位网格时(图2),节点之间的间隙须满足式(7)和式(8)条件才能保证收敛。式中r为模型FSI边界节点间的相对距离,当0.001≤r<1时,流体节点会自动移到结构界面上,这样可同时保证计算收敛性和精度的要求。定义FSI边界流体节点到结构界面的相对距离rf:

式中df为流体节点到结构边界距离;Ds为结构边界单元大小。

图2 结构与流体的FSI边界示意Fig.2 FSI boundary of fluid and structure
类似的,定义结构节点到流体边界的距离rs:

式中ds为结构节点到流体边界的距离;Df为流体边界上单元的长度。
2 算例概况
单层索网幕墙位于宜兴东氿大厦建筑入口位置,高度为24.64 m,宽度为26.0 m。该结构在构造上包括预应力拉索、连接爪件、玻璃面板3部分。玻璃的4个角点通过爪件和索连接,玻璃和玻璃之间采用硅酮密封胶连接。其传力路径为:风荷载→玻璃面板→驳接爪件→预应力索→基础主体结构。玻璃采用8 mm+8 mm的双层夹胶玻璃,分格列数为17,行数为16。第一列和最后一列的分格尺寸为1 750 mm×1 540 mm,中间部分的分格尺寸为:1 500 mm×1 540 mm。竖索预拉力为150 kN,索径36 mm,预应力为147.5 N/mm2;横索预拉力为120 kN,索径30 mm,预应力为170 N/mm2。

图3 建筑效果图Fig.3 Build preview
3 单层索网及单层索网玻璃幕墙动力特性分析
3.1 有限元模型及结构静力性能分析
采用通用有限元软件ADINA建立包含玻璃面板、索网、爪件、密封胶在内的玻璃-索网结构整体计算模型(图4)。索网结构采用杆单元,驳接爪件采用梁单元,密封胶采用壳单元模拟。面板和索网通过梁单元模拟的爪件连接协同工作,索两端采用铰接约束。索单元以初应变的方式施加预应力模拟索张力形成结构初始刚度。


图4 索网幕墙有限元计算模型Fig.4 Finite element model
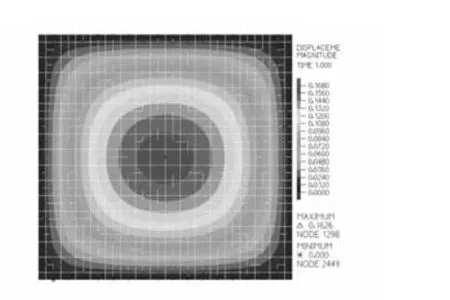
图5 索网幕墙静力位移云图Fig.5 Static-displacement nephogram
建筑所处地方为B类地貌,根据《建筑结构荷载规范》W0=450 N/m2,施加在玻璃面板上,玻璃面板与索网整体协调变形,最大位移为0.162 1 m,位于玻璃面板中点(图5)。不考虑玻璃面板,将450 N/m2的基本风压按照玻璃面积转化为节点荷载施加在索网节点上,由于结构刚度减小,荷载作用下最大节点位移为0.208 6 m。
3.2 动力特性分析
玻璃面板未施加风荷载,通过动力特性分析得到前8阶振型(图6)以及频率(表1)。根据文献[12]可知,玻璃幕墙第1阶振型能量占总振型能量的60%左右,前5阶占到90%以上。根据Rayleigh阻尼公式,由第1、5阶频率计算结构阻尼,用于流固耦合计算的结构模型。
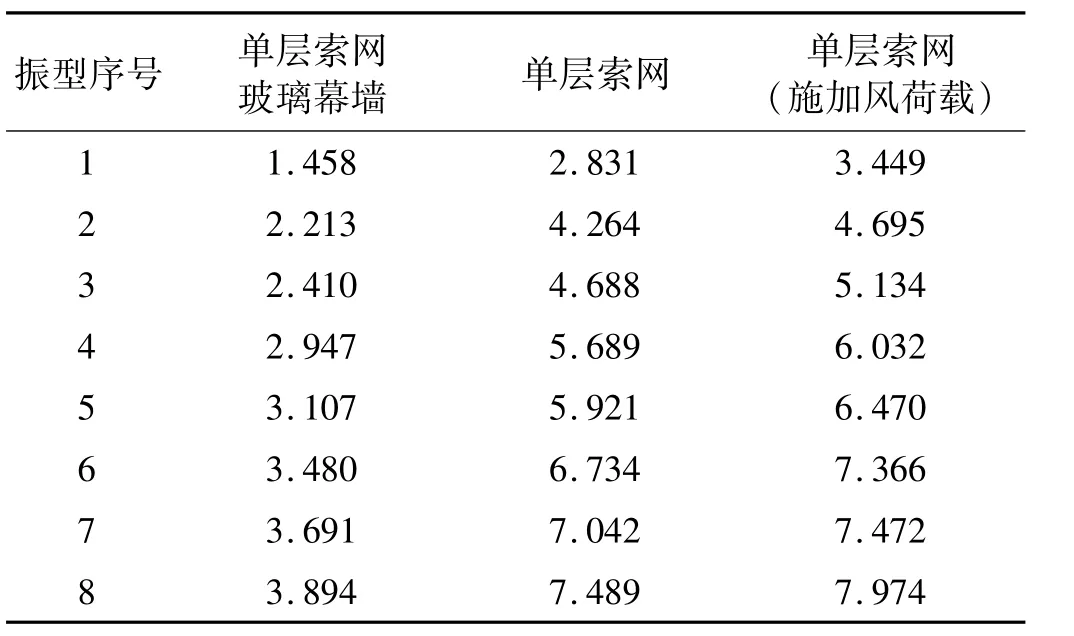
表1 索网幕墙及索网前8阶频率Tab.1 Cable net facade and cable net frequency
不考虑玻璃面板作用,对单层索网进行振动特性分析,由于结构质量比刚度减小更为显著,与索网幕墙计算结果相比,索网结构频率增大,结构振型没有变化。
考虑结构实际受荷情况,将风荷载换算为节点荷载施加在单层索网上,由于变形增大、应力刚度增加,结构频率进一步增大(表1)。

图6 索网玻璃幕墙1-8阶振型图Fig.6 Vibration modes
4 单层索网玻璃幕墙风振响应分析——FSI
采用迭代耦合方法,将计算域分为结构域(CSD)和流体域(CFD),流体压力施加在流固耦合面上导致结构变形,结构变形进一步改变流场分布,二者通过流固耦合面交换压力、位移等数据,如此反复直到计算收敛。CSD模型参考3.1节。
4.1 CFD计算模型
考虑玻璃幕墙周围建筑,将玻璃幕墙及S型裙房放置在流场中。将流域分成核心区和外围流场两部分(图7),核心区为Tetra网格,近壁区沿建筑表面法线方向劈分10层网格,边界层最小层体网格尺度为0.2 m,按1∶1.2过渡。全场最终网格约84万,节点数约41万。

图7 流场网格划分示意图Fig.7 Grid of fluid domain
4.2 流固耦合(FSI)模型
湍流模型采用LES-Smagorinsky;时间积分格式为Bathe-Composite;空间离散格式为二阶;收敛容差不低于1e-4。
采用湍流尺度沿高度不变的Davenport风速谱,由AR模型生成脉动风速时程(模型阶数P=4),施加在流场入口[17],如图8所示,风速谱与目标谱吻合;脉动风速时程平均值为27 m/s,风速剖面沿高度不变。出口采用自由出口边界条件;地面及玻璃幕墙周围建筑设置为无滑移固壁;侧壁及流场顶部约束法向速度;流固耦合面为索网幕墙玻璃面板。

图8 脉动风速功率谱Fig.8 Power spectrum
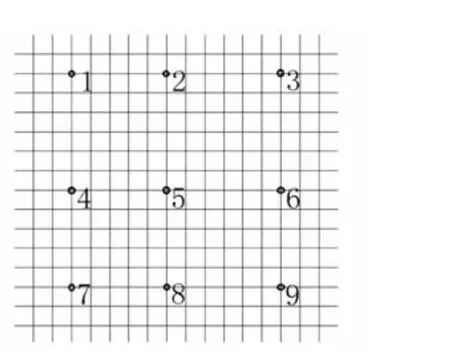
图9 测点布置Fig.9 measuring points arrangement
4.3 风致动力响应结果分析
在玻璃面板上布置9个测点(图9),提取风荷载作用下测点位移和压力时程,进行统计分析,相关结果见表2。计算结果表明,结构平均位移最大值为0.156 m,位于玻璃面板中部。基本风压W0=450 N/m2的静力荷载作用下(图4),结构最大位移为0.162 m,考虑体型系数(整体分布值大约为0.90),二者很接近。由此可判断,瞬态FSI计算模型具有合理性。

表2 测点位移及风压统计结果Tab.2 Nodal displacement and pressure statics
提取测点5的位移、加速度和节点压力,并进行频域分析,得到位移幅值谱和加速度功率谱(图10)。由位移幅值谱可知,在脉动风荷载作用下,索网幕墙主要做受迫振动,以背景响应为主;由加速度功率谱可知,在脉动风作用下,前几阶模态激发明显,有一定共振响应特征,总体表现为窄带响应过程。

图10 测点时程数据及谱分析Fig.10 Nodal time history data and spectrum analysis
5 单层索网风致动力响应分析—频域法
平均风荷载作用下,索网达到新平衡位置,在脉动风荷载作用下做弱幅振动,近似认为结构为线性,以此时对应的结构参数为基准,采用线性频域分析方法对索网进行风振响应分析。
仅考虑单层索网,利用3D3S软件建立有限元模型,共划分节点302个,模型参数参照第3节。采用Davenport风速谱,建筑所处地区属B类地貌取k=0.003,平均风速为27 m/s;平均风压0.450 kN/m2;各结点体型系数取0.90。提取平均风荷载作用下索网前200阶模态,空间相关系数取用与频率相关的Davenport相干函数,采用振型分解组合法(SRSS),由公式(9)计算位移方差:


图11 索网脉动位移峰值分布Fig.11 Peak value distribution of fluctuating displacement
为得到一定保证率下的脉动位移峰值,由公式y=μσy计算得到,其中σy为位移根方差,μ为保证系数(峰因子)。我国规范保证系数(峰因子)取值为2.2(保证率98.61%)。图11为索网脉动位移峰值分布,最大脉动位移峰值为118.7 mm(位移根方差为54.0 mm)位于索网中部。
采用流固耦合分析方法,位移根方差最大值发生在玻璃面板中部测点5附近(图8),扣除位移平均值,其脉动位移最大值为226 mm-154 mm=72 mm,测点位移根方差为23.5 mm。
对比分析可知,由于流固耦合计算考虑了玻璃面板,结构刚度加大,结构平均位移和风振响应与纯索网结果相比都有所减小;不考虑玻璃刚度,采用频域法计算索网脉动位移较大,结果偏于保守。
6 结 论
(1)考虑玻璃,单层索网刚度增加,索网的静力位移减小;不考虑玻璃面板,结构振型参与质量减小的影响更显著,单层索网频率大于索网幕墙频率。
(2)根据流固耦合理论建立了FSI模型,对索网玻璃幕墙进行风致动力响应分析,结果表明,结构主要做受迫振动,振动为窄带过程。
(3)采用频域方法分析单层索网的脉动响应,与瞬态FSI计算结果对比可知,玻璃面板减小了结构的平均位移和脉动响应,不考虑玻璃面板的频域法计算结果偏于保守。
[1]冯若强,冀鹏,武岳,等.单索幕墙中玻璃与索静力协同工作试验[J].哈尔滨工业大学学报,2006,38(12):2065-2069.
FENG Ruo-qiang,JIPeng,WUYue,etal.Static mechanism of glass work in cooperation with cable net in monolayer cable net glass curtain.[J].Journal of Harbin Institute of Technology,2006,38(12):2065-2069.
[2]冯若强,武岳,沈世钊,等.考虑玻璃参与工作的单层平面索网幕墙结构静力性能研究[J].建筑结构学报,2005,26(4):99-106.
FENG Ruo-qiang,JIPeng,WUYue,etal.Static performance of single-layer plane cable net glass curtain in consideration ofglasspanel[J].JournalofBuilding structures,2005,26(4):99-106.
[3]FengRuo-qiang,WuYue,ShenShi-zhao.Working mechanism of single-layer cable net supported glass curtain walls[J].Advances in Structural Engineering,2007,10 (2):183-195.
[4]FengRuo-qiang,WuYue,ShenShi-zhao.Geometric nonlinearity of cable net facade[J].Chinese Journal of Computational Mechanics,2008,25(5):640-646.
[5]杨立军,何志鹃,陆守明.单层正交索网结构承载性能研究[J].四川建筑科学研究,2008,34(1):33-35.
YANG Li-jun,HE Zhi-juan,LU Shou-min.Study of loadbearing capacityforsingle-layerorthogonalcablemesh structure[J].Sichuan Building Science,2008,25(5):640 -646.
[6]王元清,孙芬,石永久,等.玻璃及节点约束对单层索网承载性能的影响[J].哈尔滨工业大学学报,2007,39 (8):1309-1313.
WANG Yuan-qing,SUN Fen,SHI Yong-jiu,et al.Influence of glass and joint constraint on loading capacity of monolayer cable net for point supported glass buildings[J].Journal of Harbin Institute of Technology,2007,39(8):1309-1313.
[7]Wang Yuan-qing,Wu Li-li,Shi Yong-jiu.FEM analysis and experimental study on monolayer cable net for glass facades:static performance[J].Advances in Structural Engineering,2007,10(4):371-382.
[8]冯若强,武岳,沈世钊.单层平面索网结构非线性频率简化计算方法研究[J].工程力学,2007,24(10):87-91.
FENG Ruo-qiang,WU Yue,SHEN Shi-zhao.Study on simplified calculation method of nonlinear frequency of singlelayer cable net.[J].Engineering Mechanics,2007,24 (10):87-91.
[9]吴丽丽,王元清,石永久,等.点支式玻璃建筑单层索网体系的动力特性[J].清华大学学报(自然科学版),2006,46(3):318-321.
WU Li-li,WANG Yuan-qing,SHI Yong-jiu,et al.Dynamic characteristics of monolayer cable net for dot point glass facade[J].J Tsinghua Univ(Sci&Tech),2006,46(3):318-321.
[10]Shi Yongjiu,Wu Lili,Wang Yuanqing.FEM analysisand experimental study on monolayer cable net for glass facades:dynamic property[J].Advances in Structural Engineering,2007,10(4):383-395.
[11]冯若强,花定兴,武岳,等.单层平面索网幕墙结构玻璃与索网协同工作的动力性能研究[J].土木工程学报,2007,40(10):27-33.
FENG Ruo-qiang,HUADing-xing,WUYue,etal.Dynamic performance of cable net facade with consideration of glass panels[J].China Civil Engineering Journal,2007,40(10):27-33.
[12]吴丽丽,王元清,石永久.单层平面索网幕墙结构的风振响应特性分析[J].工程力学,2007,24(增刊Ⅰ):98-103.
WU Li-li,WANG Yuan-qing,SHI Yong-jiu.Research on wind-induced response behavior of monolayer cable net for glass facades[J].Engineering Mechanics,2007,24:98 -103.
[13]冯若强,武岳,沈世钊.单层平面索网幕墙结构的风激动力性能研究[J].哈尔滨工业大学学报,2006,38(2):153-155.
FENG Ruo-qiang,WU Yue,SHEN Shi-zhao.Wind-induced dynam ic performance of cable net glazing[J].Journal of Harbin Institute of Technology,2006,38(2):153-155.
[14]吴丽丽,王元清,石永久.单层平面索网结构风振响应的几何非线性特性研究[J].振动与冲击,2007,26(4):30 -34.
WU Li-li,WANG Yuan-qing,SHI Yong-jiu.Study on nonlinear characteristicsofwind-inducedresponseofa monolayer cable net system[J].Journal of Vibration and Shock,2007,26(4):30-34.
[15]Adina Theory and Modeling Guide[M].ADINA R&D,Inc.,2005.
[16]玻璃幕墙工程技术规范[S].JGJ 102—2003.北京:中国建筑工业出版社,2003.
[17]余志祥.高速铁路大型客站建筑风荷载及流固耦合作用研究[D].成都:西南交通大学,2011:132-166.
Influence of glass on dynamic response of a monolayer cable net
YAN Yan-jun1,2,YU Zhi-xiang3,LI Han1,ZHANG Qi-lin1
(1.College of Civil Engineering Tongji University,Shanghai 200092,China;2.Shanghai Construction No.7(Group)Co.,Ltd.Shanghai 200050,China;3.School of Civil Engineering,Southwest Jiaotong University,Chengdu 611756,China)
In order to ensure glass deformation coordinated with a cable net,a FE model including a glass panel,a cable net,sealants,and spider was established to study the influence of glass panel on the static performance and dynamic characters of the cable net.The flowing field was simulated considering the buildings around the glass curtain wall.Based on those,fluid-structure interaction(FSI)analysis was performed to study the spectrum characteristics,dynamic response of the glass curtain wall.Under the average wind load,the cable net reached a new equilibrium position,the windinduced response of the structure was studied with the frequency domain method.Comparison of two methods results showed that under wind load,the structure forced vibration is a narrow band process;the glass panel effectively reduces the average displacement and pulse response of the cable net.
glass panel;glass curtain wall of a monolayer cable-net;FSI;frequency domain method
TU383
A
10.13465/j.cnki.jvs.2014.23.005
“十二五”科技支撑计划(2011BAJ08B10);国家自然科学基金项目(51378428);中央高校基金青年科技创新项目(A0920502051208-61)
2013-09-12 修改稿收到日期:2013-11-28
闫雁军男,博士生,1983年6月生
余志祥男,副教授,硕士生导师

