直线振动筛出料梁的模态分析
孙皆宜
(唐山学院 基础教学部,河北 唐山063000)
0 引言
直线振动筛通过激振器带动筛箱做快速往复振动进行工作,是关键的洗煤设备之一[1]。由于大型直线振动筛在重载和振动的状态下工作,筛梁常常会出现各种故障,甚至由于自身共振使结构遭到破坏(如出现裂缝等),因此振动筛的动态设计要求梁具有足够的强度和一定的固有频率及振型,以有效地避开激振器的工作频率,防止振动筛在运行过程中筛梁发生共振。有限元模态分析能为各产品的结构设计和性能评估提供一个强有力的工具,其可靠的实验结果往往可作为产品性能评估的有效标准[2-3]。在振动筛箱体结构中,出料梁和入料梁对箱体结构的稳定性起着重要的作用,出料梁和入料梁的结构相似,本文主要针对出料梁进行模态分析,考察出料梁的自身振动特性。
1 模态分析理论
模态是结构自身的固有振动特性,每一阶模态都具有特定的固有频率、阻尼比和振型。模态分析是对结构的固有频率、阻尼比、振型进行分析的一种方法,通过它能确定结构的自然频率、振型等参数。模态分析的过程为:为了使线性非时变系统振动微分方程解耦,变成独立的以模态坐标及模态参数描述的方程,用模态坐标代替矩阵中的物理坐标,并将坐标变换矩阵作为每列即为各阶振型的振型矩阵[4]。模态分析可以得到结构的固有频率和模态振型。对于一个n自由度的机械结构,其受迫振动的微分方程为:

式中,[M]为机械结构的质量矩阵;[C]为机械结构的阻尼矩阵;[K]为机械结构的刚度矩阵。
对于该出料梁,其无阻尼振动方程为:

出料梁的[M]和[K]都保持为常矩阵。当发生简谐运动,即u=U sin(ωt)时,方程式(2)可转化为

方程(3)的特征值平方根ωi就是出料梁的自然圆频率(弧度/秒),下标i从1到自由度的数目n。得到其自然频率为fi=ωi/2π,其对应的特征向量{ui}表示出料梁的振型,即假定出料梁以频率fi振动时的振幅。
2 有限元模型的建立
以一台大型直线振动筛出料梁为研究对象,利用Pro/E按1∶1的比例建立出料梁的三维模型,并去掉吊耳、倒角和紧固用的螺栓孔等以提高计算效率,如图1所示。然后将简化后的模型导入有限元分析软件ANSYS/Workbench,并设置出料梁的材料为结构钢Structural Steel,密度为7 850 kg/m3,泊松比为0.33,弹性模量为209 GPa。划分网格,得到17 243个节点和8 829个单元,如图2所示。

图1 简化的出料梁

图2 划分网格后的有限元模型
设该出料梁无预应力作用,直接在出料梁的两端施加固定约束,求解的频率范围为0~1 000 Hz,提取出料梁的模态阶数为6,进行求解。
3 模态分析结果及结论
经有限元分析求解后,得到出料梁的前6阶固有频率和对应的模态振型,如图3至图8所示。

图3 第1阶模态振型
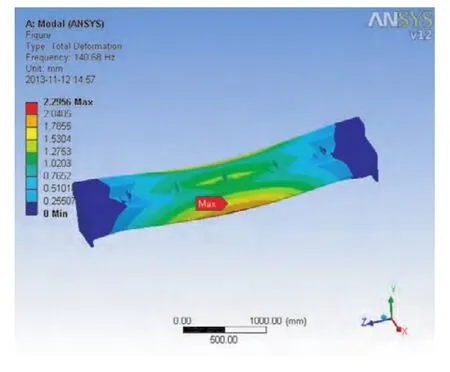
图4 第2阶模态振型
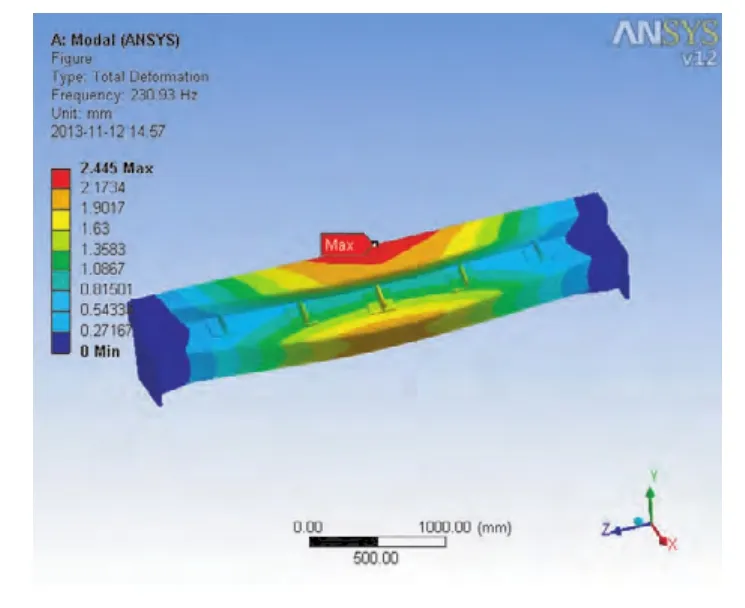
图5 第3阶模态振型
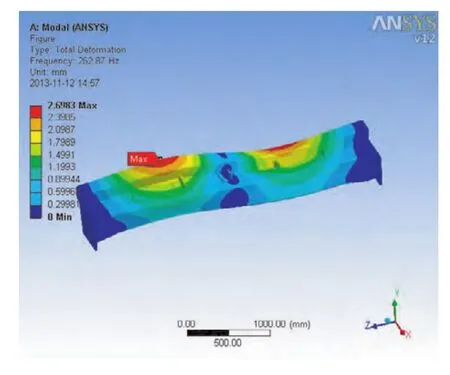
图6 第4阶模态振型

图7 第5阶模态振型
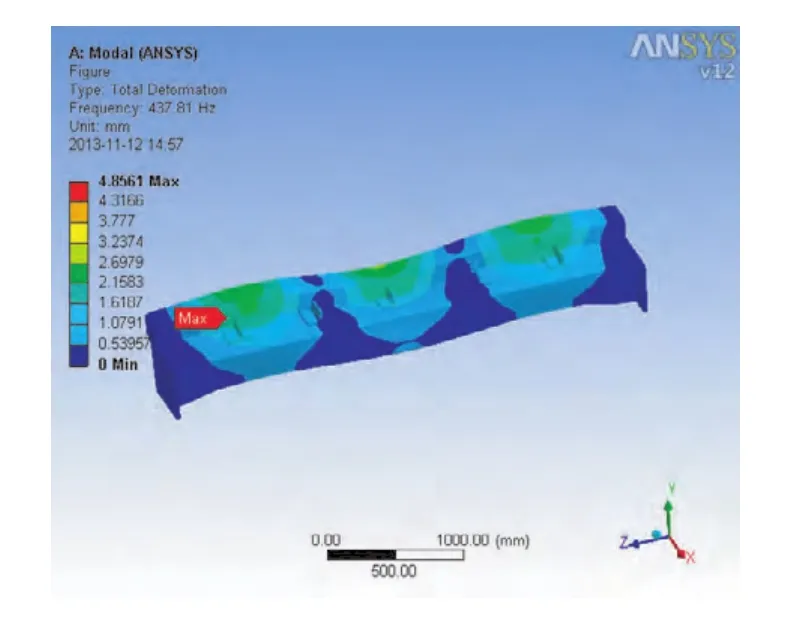
图8 第6阶模态振型
以上各阶振型图皆为具有一定比例的变形图,从中可以很清楚地看出各阶下出料梁的振型特点,得到各阶频率值见表1。

表1 出料梁模态分析结果
通过以上得到的出料梁的模态分析结果,以及前6阶振型图可知,出料梁的振动主要是沿Y轴的往复振动和沿绕Z轴的轻微扭转,这与添加的约束形式有关。出料梁的最大变形量为2.56 mm,相对其自身尺寸来讲数值很小。出料梁的第一阶频率为113.32 Hz,远远高出了振动筛的振动频率16 Hz,所以在振动筛工作过程中,不会发生出料梁自身共振现象,这样出料梁的结构不易被破坏。
[1] 和世超,赵尚民.振动筛筛框模态分析及动态响应[J].焦作工学院学报:自然科学版,2001(5):400-402.
[2] 盛和太,喻海良,范训益.ANSYS有限元原理与工程应用实例大全[M].北京:清华大学出版社,2006.
[3] 刘国庆,杨庆东.ANSYS工程应用教程:机械篇[M].北京:中国铁道出版社,2003.
[4] 陈建恩.小麦联合收割机振动试验研究[D].兰州:甘肃农业大学,2009.

