电加热炉温度监控系统的设计
吕宏丽
(唐山学院 信息工程系,河北 唐山063000)
电加热炉是科学实验、工业生产等过程中常用的加热设备,由于炉的种类和规格不同,加热对象不同,它们构成的系统千差万别。而且从控制的角度看,大多数电加热炉是滞后、惯性、特性参数随温度变化的被控对象,难以用数学模型精确表达[1]。本文以实验数据为基础,从加热炉温度控制系统的物理意义入手,分析并确定加热炉的数学模型,采取PID调节实现温度控制。
1 电加热炉温度控制系统建模
根据电加热温度控制系统的物理意义和响应特性,得到一种描述电加热炉温度控制系统的模拟模型,如图1所示[2]。
其中,Is表示电流源,模拟于电加热源(电炉丝等);C表示电容,模拟于加热体热容;R表示电阻,类比热阻;E表示外部电压值固定的电压源,模拟于外部温度;V表示炉内温度值,此值作为反馈量送往温控器;I表示温控器运算后所送出的功率值。根据文献[2]的系统建模方法,加热炉数学模型为:
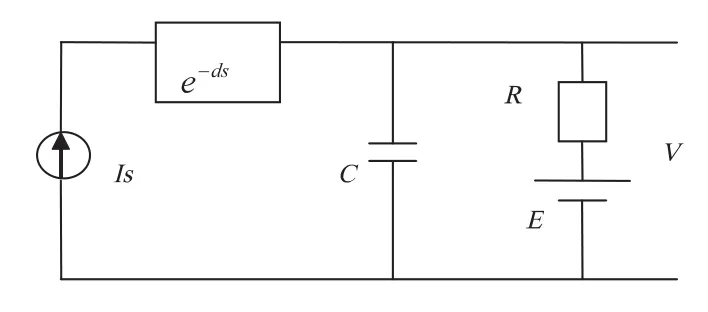
图1 加热与散热模拟模型示意图
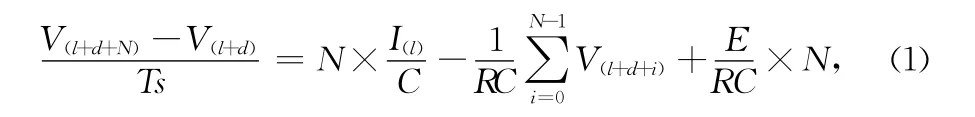
其中,Ts表示采样周期;N为正整数,表示有采样周期的个数;d表示加热器的加热时间延迟周期。当温度到达设定点时,设输入为零,因为延迟项的关系,温度仍会上升一小段,因此,从输入为零开始与系统实际温度达到峰值开始下降之间的时间差,定为本模型的延迟周期。
参数C和R需要通过自然降温过程和全量升温过程确定。利用全量升温过程可确定C,利用自然降温曲线可确定模型中的RC。
用电加热炉组成开环系统,用实验方式在5 000 s观测时间内采集输入功率和输出温度,绘制实时曲线如图2所示。每隔106.4 s存储一组数据,共读取了48组数据。所选取的温度、功率对应同一时刻的数据如下。
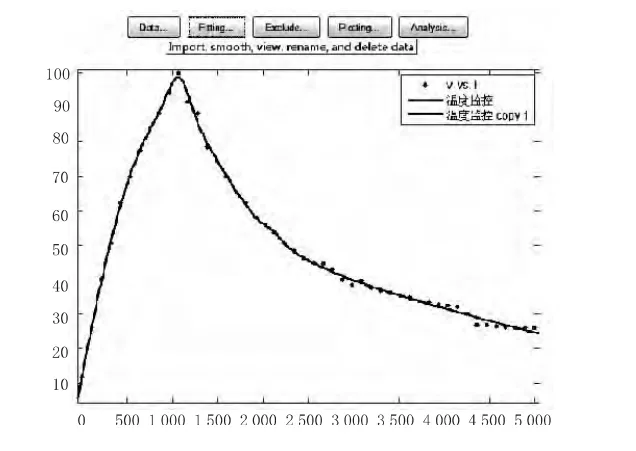
图2 功率加热升降温响应曲线
输入功 率:I = [622 1197 1914 2345 2776 3207 3447 3782 3973 4308 4500 4117 3782 3566 3351 3207 2920 2800 2681 2609 2465 2345 2250 2154 2034 1963 1939 1914 1867 1771 1699 1627 1580 1532 1484 1472 1464 1421 1388 1383 1355 1330 1316 1302 1292 1283 1269 1268]。
输出温度:y= [12.00 26.00 39.89 50.54 62.37 69.89 77.42 83.87 88.17 94.41 100.00 91.40 88.17 78.49 74.41 69.89 65.59 62.37 58.06 55.91 53.76 50.54 48.38 46.24 45.06 44.54 43.00 40.00 38.49 39.78 37.63 36.90 36.56 35.40 34.80 33.76 33.40 32.80 32.56 32.00 30.00 27.00 26.90 26.50 26.25 26.13 26.00 26.00]。
1.1 全量升温过程
在全量升温的过程中,系统为全功率升温,模型中的I恒为百分之百,将模型表达式(1)整理成:
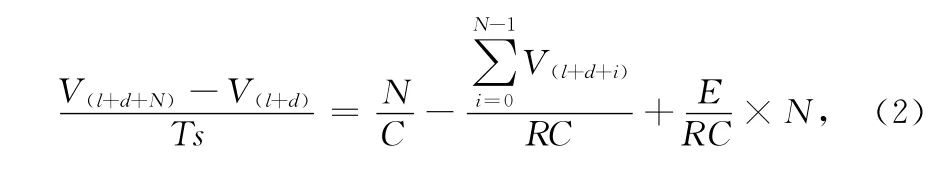
可得
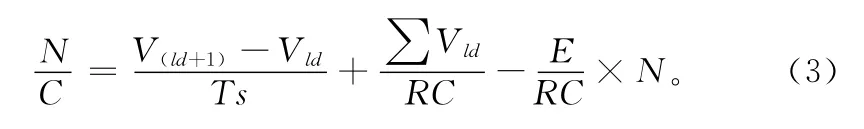
系统升温阶段对应着观测时间从0 s开始计时到1 170.2 s的相应输入输出的数据。根据建模原理的要求,取相邻的2个周期分别记做V3,V4,每个周期均取4个数据。即
V3= [12.00 26.00 39.89 50.54];
V4= [62.37 69.89 77.42 83.87]。
将数据代入公式(3),求得C=3.12。
1.2 自然降温过程
在自然降温的过程中,由于输入功率为零,即模型中的I(k-d)恒为零,故可将模型表达式(1)修改为:

假设取两个相邻的控制周期Vl,Vl+1,Vl+2,记做Vld=
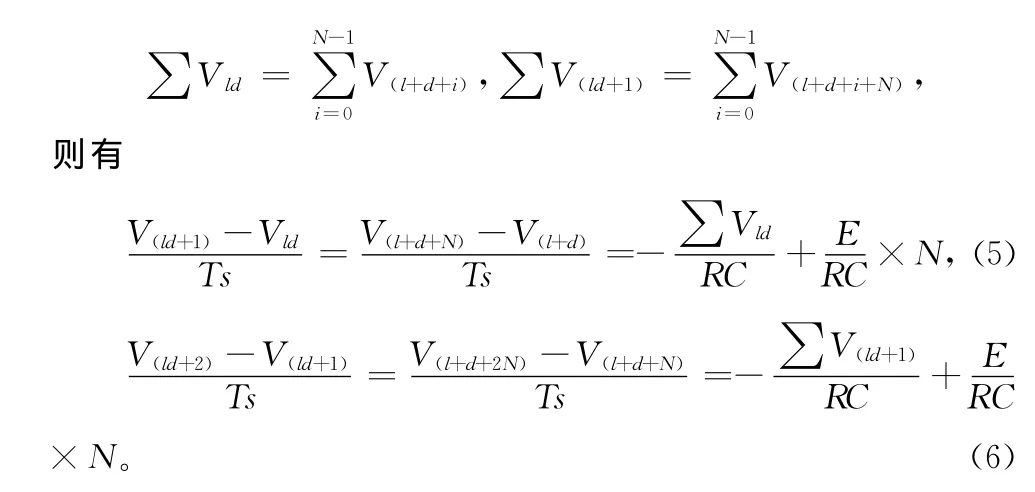
两式联立,解得(其中V可利用温度测量元件得到)

在48组数据中,系统降温阶段对应着时间计时从1 272.6 s到5 000 s的所有数据。按照建模原理要求,可以取Ts=106.4 s,N =5,取相邻的3个周期分别记做V0,V1,V2,所选取的相应数据分别为:
V0= [91.40 88.17 78.49 74.41 69.89];
V1= [65.59 62.37 58.06 55.91 53.76];
V2= [50.54 48.38 46.24 45.06 44.54]。
将C=3.12代入RC=2 115,得到R=678。
同时通过实验操作测得本次数据采集中延迟时间d=72 s。根据实验得到的各种参数确定加热炉数学模型的表达式如下:

2 温度控制系统设计
电加热炉炉膛温度是由炉丝的供电功率调节的,炉丝由固态继电器的导通/关断控制供电。通过调节器改变占空比可以实现输出功率的调节,从而调节电加热炉炉膛温度。电加热炉温度控制系统的控制原理如图3所示。
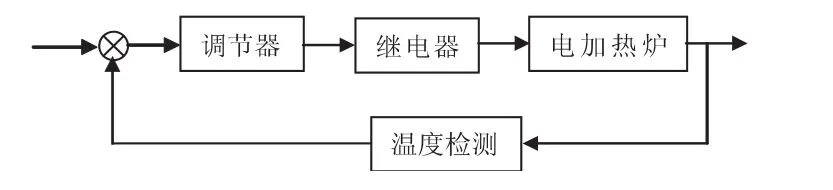
图3 电加热炉温度控制系统原理图
调节器采用传统的PID控制,PID参数的整定采用稳定边界法[3],如表1所示。

表1 稳定边界法的PID参数关系
上表中,Km表示系统增益,ωm表示振荡角频率。根据电加热炉的数学模型,利用Matlab软件建模,确定出PID控制器的相应参数:Kp=7.5,Ti=0.025,Td=5。
3 温度监控系统设计
温度控制系统采用S7-200 PLC实现,利用MCGS组态软件[4]设计监控界面。图4为温度监控系统界面。

图4 加热炉温度监控界面
在MCGS界面上点击“开始实验”按钮,系统开始运行。系统将从室温开始,全功率加热到100℃。停止加热,之后进入自然降温过程,并设定系统稳定温度为80℃。在比例增益为7.5,积分系数为0.025,微分系数为5的设定条件下,实时记录电加热炉炉膛温度,观测实时曲线,系统的实时升温降温曲线如图5所示。
4 结论
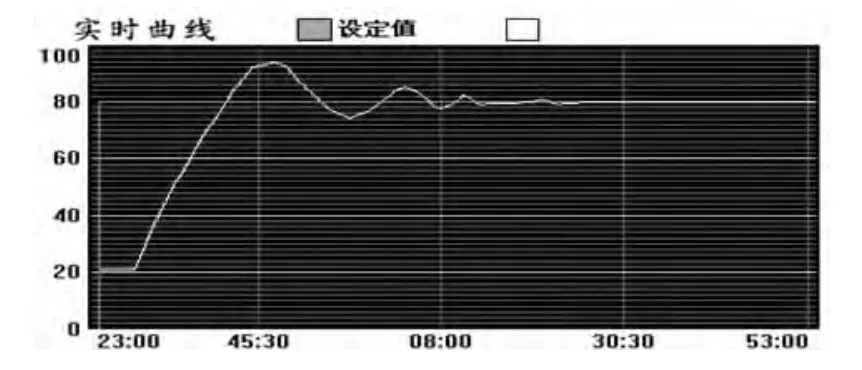
图5 系统的实时升温降温曲线
实验数据验证了加热炉控制系统模型的可靠性。控制系统模型整定的PID参数可以使系统在运行过程中较快地达到稳定过程。在实际电加热炉温度控制系统中,可以根据系统的稳定工作的温度段,通过进一步精细调整模型参数,在一定温度段上使系统性能更加精进。
[1] 王再英.过程控制系统与仪表[M].北京:机械工业出版社,2006.
[2] 李林琛,杨晓雪.电加热炉温度控制系统数学模型的建立及验证[J].北京工业职业技术学院学报,2010(10):21-25.
[3] 刘金琨.先进PID控制 MATLAB仿真[M].北京:电子工业出版社,2004.
[4] 马国华.监控组态软件及其应用[M].北京:清华大学出版社,2001.

