永磁同步电机调速控制系统研究
李 兵,姚明林,冯曰臻
(1.唐山学院,河北 唐山063000;2.河北联合大学 信息学院,河北 唐山063009)
0 引言
永磁同步电机具有启动性能好、转子转动惯量小、散热性好等优点,被广泛应用于电动车、工业机器人以及电梯升降设备之中。速度控制是永磁同步电机的核心问题。传统的速度控制方法,如比例积分(PI)控制方法,虽然有着结构简单的优点,但是对于机械参数变化与负载干扰的影响,其控制效果并不理想。近年来也有许多新的方法产生,如利用神经网络算法、变结构算法、模糊逻辑算法等多种方法对控制器进行设计,但单纯利用上述智能算法对速度进行调节,却存在运算量大,控制精度难以保证的现象。对于永磁同步电机的驱动器设计,传统方法采用正弦脉宽调制(SPWM)方法,利用控制器产生正弦的三相命令与标准三角波进行比较,应用其差异进行脉宽调制,但是所产生的电压或电流会造成谐波失真。而空间矢量脉宽调制(SVPWM)技术则是利用直流电压产生一个三相电压源的发转换,更能有效利用电能,减少奇次谐波的损失。因此本研究设计了一个永磁同步电动机双闭环调速系统,在SVPWM技术的基础上,采用模糊算法对PI控制器的参数进行自动调节,以提高系统的鲁棒性。
1 永磁同步电机的数学模型
永磁同步电机的定子与转子间相互耦合,受转子位置变化的影响,使得永磁同步电机难以控制。随着向量控制理论的提出,使得原本非线性且相互耦合的数学模型能够转换成为两轴正交的坐标系统进而简化的数学模型。
分析永磁同步电机时,最常用的是d-q坐标系的数学模型,它不仅可用于分析正弦波永磁同步电机的稳态运行性能,还能够用于分析电机的瞬态性能[1]。
在建立永磁同步电机的数学模型时通常假设:①忽略电机铁心的饱和;②不计电机中的涡流和磁滞损耗;③电机的电流为对称的三相交流电流;④ 转子上不存在阻尼绕组[2]。由此可得到永磁同步电机的定子电压方程:

式中,ud,uq为直轴、交轴电压;id,iq为直轴、交轴电流;R 为定子每相绕组相电阻;Ψd,Ψq为直轴、交轴定子磁链;ω为电动机的转子角速度;p为微分算子。
定子磁链方程:

式中,Ld,Lq为定子直轴、交轴的等效绕组电感;Ψf为永磁体产生的磁链。
电磁转矩方程:

式中,np为电机的极对数;Te为电机电磁转矩。
2 SVPWM技术
空间矢量脉宽调制技术,也称为磁链跟踪控制技术,当永磁同步电机的三相绕组上加载三相对称正弦交流电压时,会在电机的定子侧产生一个幅值恒定的定子电压空间矢量,并以正弦波相电压的角频率作为运动的角速度,矢量端点的运动轨迹为一个圆。根据电机学原理,在幅值不变,相角连续变化的电压空间矢量才能产生理想圆形的定子磁链[3]。该技术能够克服传统SPWM技术中电流或电压的谐波失真问题,同时提高电能的利用率。本设计将SVPWM技术运用在控制系统中的电流环内,对检测的电流进行追踪,从而更好控制电机。
SVPWM技术是利用逆变器输出的8种基本电压空间矢量交替作用,使输出的合成电压矢量产生期望的圆形磁链轨迹。如果在逆变器的一个周期内,6个非零基本电压空间矢量各输出一次后,输出的定子磁链矢量的矢量端点的运动轨迹是一个正六边形,如图1所示。而我们所希望的是圆形的磁链轨迹,为了获得准圆形磁链轨迹,利用这8种基本电压空间矢量的线性组合,获得更多的等幅不同相的电压空间矢量,增加逆变器开关状态,使输出的定子磁链矢量端点的运动轨迹逼近圆形旋转磁场的磁链轨迹。

图1 基本电压空间矢量形成的磁链轨迹图
3 基于矢量控制的永磁同步电机调速系统
基于矢量控制的永磁同步电机调速控制系统采用电流-转速双闭环控制,系统结构图如图2所示。转子的实际值n与给定值n*之间的差值作为误差信号输入给转速调节器。实际检测到的电机三相定子电流iA,iB,iC经过Clarke变换由三相坐标系变换成静止坐标α-β轴系中的两相电流iα,iβ,再经过Park变换得到旋转坐标d-q轴系中电流id、iq,将得到的iq与转速调节器的输出相比较,得到的差值作为电流调节器的输入。电流调节器的输出通过Park逆变换后输入至SVPWM和逆变器,SVPWM可输出6路PWM信号驱动逆变器的6个功率开关器件,不同的导通模式产生不同的空间电压基本矢量。这些基本矢量合成一组等幅不同相的空间电压矢量,使输出的电压在电机中产生的实际磁通尽可能地逼近理想磁通圆,从而更好地控制永磁同步电动机。

图2 基于矢量控制的永磁同步电机调速系统结构图
图2中ASR为转速调节器,采用模糊PI控制方法,利用模糊算法自动调整PI控制器中的比例系数与积分系数;ACR为电流调节器,采用传统的PI控制方法;SVPWM为空间矢量脉宽调制,逆变器采用电压型逆变电路。
3.1 传统PI控制
传统的离散数字PI控制的数学表达式为

式中,Kp为比例系数;Ki是积分系数;e为系统的误差。
采用传统PI控制时,Kp,Ki这两个参数是唯一确定的,不会随e,ec的变化而调整,当面对比较复杂的控制过程时,传统的PI控制方法不能够准确、快速地响应系统的变化,所以引入了智能控制方法。常见方法主要有模糊算法、专家系统、神经网络算法以及遗传算法等。综合考虑控制的快速性、准确性以及实现的简易性,设计中利用模糊算法对PI控制器的比例系数及积分系数进行自动调节,从而提高系统响应的快速性及鲁棒性。
3.2 模糊PI控制
自适应模糊PID控制器结构图如图3所示。转速环中的模糊PI控制器,以误差E和误差变化率EC为输入,根据模糊控制规则找出kp和ki与E和EC之间的关系,在运行中不断检测E和EC,对比例系数和积分系数进行在线调整,使这两个参数满足不同E和EC时的要求[3]。

图3 自适应模糊PID控制器结构图
对于不同的E,EC,PI控制器的参数kp,ki的数值也不同。模糊控制器以E和EC作为输入语言变量,kp,ki作为输出语言变量。将E,EC,kp和ki的语言变量值取{NB(负大),NM(负 中 ),NS(负 小 ),Z(零 ),PS(正 小 ),PM(正 中 ),PB(正大)}7个模糊值。将输入和输出语言变量的论域定义为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。
kp和ki的模糊控制规则表分别如表1,表2所示。

表1 k p的模糊控制规则表
设置模糊控制器语言变量为三角形隶属函数,选择最大-最小合成方法作为模糊蕴含关系,根据模糊控制规则表,采用加权平均法去模糊化后,得到Kp,Ki动态的整定参数为kp,ki。假设kp′,ki′为采用常规整定方法得到参数预整定值,控制器的参数为
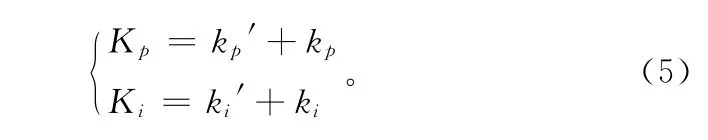
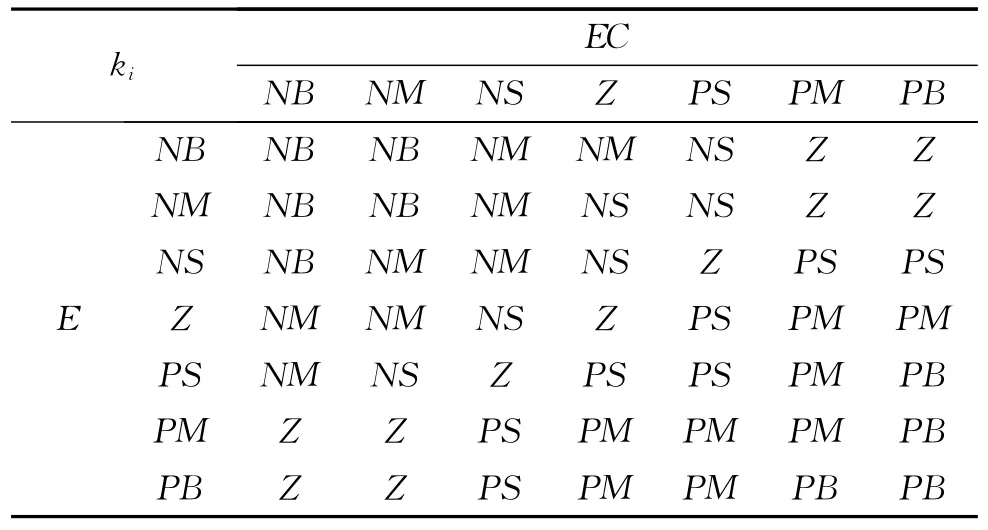
表2 ki的模糊控制规则表
4 在线运行结果分析
利用FPGA芯片进行控制器的设计。系统的硬件结构如图4所示。利用该系统对上述理论进行在线运行测试,测试过程分为两部分,第一部分进行电流回路测试,主要是测试SVPWM的控制效果;第二部分是系统整体运行调试,主要对模糊PI控制器的稳定性、快速性及准确性进行测试,并与传统PID控制器的控制效果进行比较。

图4 系统整体硬件结构
4.1 SVPWM运行测试
永磁同步电机在测试过程中,为了产生最大的转矩,必须将d轴的电流设定为零,然后通过控制q轴电流和负载来控制电机转矩大小。测试过程中有3种测试情况:
(a)q轴电流命令i*q=4 A并加载1.0 N/m负载;
(b)q轴电流命令i*q=6 A并加载1.5 N/m负载;
(c)q轴电流命令i*q=8 A并加载2.0 N/m负载。
测试中,PI控制器在d轴的参数设定为kp=0.683 6,ki=0.014 65,而q轴从参数 设 定为kp=0.781 25,ki=0.224 4。DC电压为100 V。
由运行结果(图5-7)可以看出,在不同电流命令及不同负载下,反馈电流能够以旋转磁场形式追踪电流命令,通过电路转换后,输出的实际电压能够很好地逼近磁通圆,并且基本上没有奇次谐波。
4.2 系统整体运行结果
此回路测试均在负载为1.0 N/m的情况下,以不同转速命令分别对传统PI控制器及模糊PI控制器进行测试比较,测试结果如表3所示。

图5 电流命令为4 A,负载为1.0 N/m时的旋转磁场电压与电流
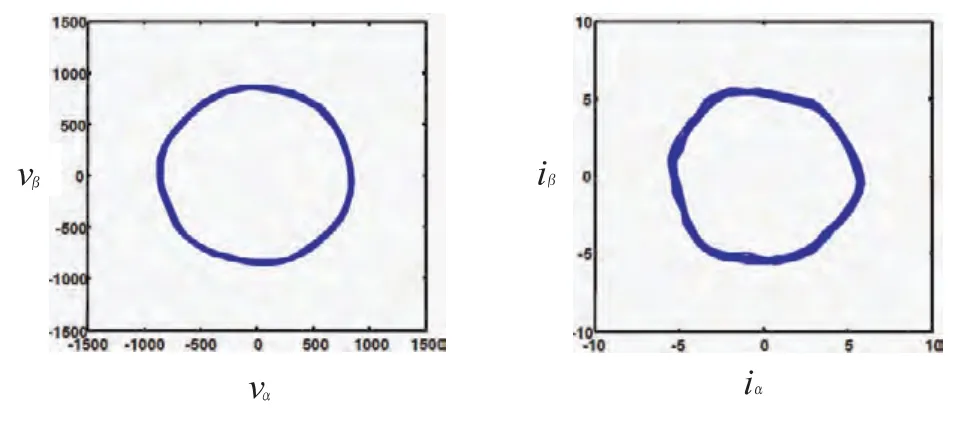
图6 电流命令为6 A,负载为1.5 N/m时的旋转磁场电压与电流

图7 电流命令为8 A,负载为2.0 N/m时的旋转磁场电压与电流
由测试结果可以看出,利用模糊PI控制器对速度进行控制,其效果在系统响应速度、稳定性及准确性等各项指标中均优于传统的PI控制器。

表3 采用两种方法得出测试结果的比较
5 结论
在向量控制理论的基础上,利用模糊PI控制器对电机转速进行调节,通过系统运行数据的比较,该方法在性能上优于传统的PI方法。同时,在电流控制回路中采用了SVPWM技术,电流追踪效果良好,并且减小了奇次谐波的损耗,提高了电能的利用率。此控制系统可以在较大的转速范围内进行快速精确的调节,能够满足现场设备的精准控制要求。
[1] 李崇坚.交流同步电机调速系统[M].北京:科学出版社,2006:132-145.
[2] 陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2003:178-187.
[3] 袁登科,陶生桂.交流永磁电机变频调速系统[M].北京:机械工业出版社,2011:77-90.
[4] Li Chongjian.AC Synchronous motor speed control system[M].Beijing:Science Press,2006:112-115.
[5] Zhang Yaou,Zhao Wansheng,Kang Xiaoming.Control of the permanent magnet synchnonous motor using mode reference dynamic inversin[J].Wseas transactions on system and control,2010(5):302.

