压力传感器零点温漂的两种补偿方法比较

吴 峰

(中煤科工集团上海研究院，上海201400)

压阻式压力传感器以其灵敏度高、动态响应好、性能可靠、精度高、功耗低、易于微型化与集成化等优点被广泛应用于工业生产的各个领域，其误差也直接影响到测控设备的性能。目前制造压阻式压力传感器一般采用半导体材料，温度成了影响其工作性能的最主要因素之一，正因为如此，其应用多采用四个桥臂的差动等臂等应变全桥检测模式。由于制造工艺中光刻、制版、扩散等工艺的偏差而出现阻值差异和电阻温度系数差异，要设计相等的四臂电桥必须对零位偏移和零位温度漂移进行补偿。解决好这个问题是压阻式压力传感器确保精确测量压力的基础。本文在前人研究的基础上，通过推导与分析对一种硬件补偿和一种软件补偿方法进行比较。

1 硬件电路补偿

1.1 恒压源供电下的电桥输出

图1 恒压源供电的压阻力敏全桥

图1为恒压源供电的压阻电桥，桥压为Ue。其中R1、R3受压后产生负应变，R2、R4受压后产生正应变，其温度系数分别为α1～α4，受压后的电阻变化量均为ΔR。在近似处理时，四臂电阻值均视作R。那么在未受任何压力情况下由于桥臂失衡产生的零位输出电压［2］为

由式(1)可以看出，零位平衡的条件为相对桥臂上电阻的乘积相等。在温度变化Δt后的零位温度漂移量为

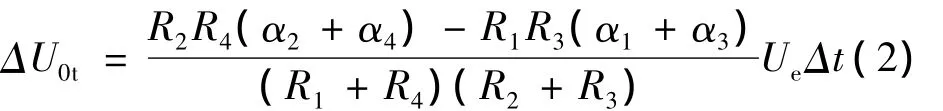
由式(2)看出使得零位温度漂移最小的条件是在满足相对桥臂电阻乘积相等的同时，相对桥臂上电阻的温度系数之和也必须相等。

1.2 零位调整和零位温度系数补偿

在实际生产制造时由于制造工艺产生的偏差不可能实现四臂电桥完全相等，因而出现阻值差异与电阻温度系数差异，因此必须对零位偏离和零位温度漂移进行补偿。

压阻式传感器设计中通常采取在其中两个桥臂上分别串联一个电阻和并联一个电阻的方法［3］，即可同时实现平衡零位和补偿零位漂移。通常选用的串并联电阻温度系数远小于扩散桥臂电阻温度系数，因此也改变了被串(并)桥臂电阻的温度系数。不难得出，当在电阻温度系数α的桥臂电阻R上串联温度系数为β、阻值为 Rs的电阻时，等效电阻 R’及温度系数 α＇［4］变为:

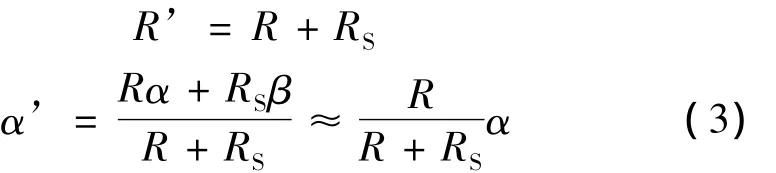
当并联一个温度系数为β的电阻RP在桥臂电阻R上时，并联后的等效电阻R’以及温度系数α’分别变为:

当并联一个RP=KR的电阻在桥臂电阻R上时，并联后的电阻温度系数变为原来的，同时阻值也变为原来的;而若串联一个R=R的电阻在桥S臂电阻R上时，串联后的电阻温度系数也减小至原值的，但阻值却为原值的倍。因此，利用在四个桥臂电阻上选择串、并联位置与阻值的方法，便可同时实现平衡零位与补偿零位漂移。具体操作为，首先测得桥臂四个电阻的常温阻值，然后测得它们在正温上补偿区点和负温下补偿区点的值，就可计算出正负温区的桥阻温度系数，计算机可按编写好的程序求解出串、并联的位置及阻值。可以采用直接测试四臂不平衡输出零位及正负温漂，然后求算出补偿位置与阻值的办法。此时，一般是尽量用并联补偿温漂，而用小阻值RS调整零位，并且为了简化计算，一般只开环一个点，即只有两个串联位置选择。

图2 半开环压阻全桥的U0调整和U0t补偿

图2给出了半开环的力敏全桥。图中，只有桥臂R1和R2上可以串联RS。当U0正漂时，RP并联在R4上，视U0正负决定RS串联位置(U0为正时RS与R1并联，反之与R2并联);当U0负漂时，RP并联于R3上，也视U0正负决定RS的串联位置。

2 软件补偿

软件补偿的算法主要有曲线拟合法与表格法。本文采用规范化多项式拟合曲线法实现对压阻式压力传感器零点偏离和零点温度漂移的补偿。结合一种压阻式压力传感器，应用多项式拟合方法对实测数据进行拟合，并根据拟合曲线求出对应温度点的输出电压与实测数据进行比较。结果表明，此方法拟合数据精度极高，补偿效果优于硬件补偿方法。

2.1 非线性函数多项式规范化拟合原理

多项式被用来拟合非线性信号时，最为关键的是各个系数的求解。输出电压的非线性函数U=f(TT0)=f(ΔT)可用一个多项式来表示:

求解式(5)中各项系数需5对电压、温差测量值，由于幂级数多项式无正交性，不仅计算起来繁琐，且不利于工程实现。现有一种规范化多项式拟合［5］，提出一种标准化方法，使得计算简便，易于编程。应用此方法对曲线进行分段拟合时，接合点连续且接合点附近分段部分重叠。具体原理如下:

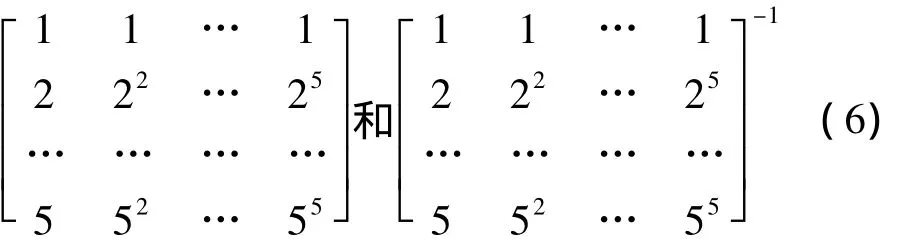
可得下式

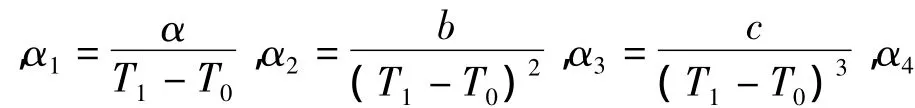
2.2 实验及结果分析

实验器材:标准压力计、温度计、压力传感器。实验时将压阻式压力传感器和温度计放入恒温槽中，温度计用于监测恒温箱温度。温度值从10℃ ～60℃范围内选取6个均匀分布的温度点记录压力传感器的输出电压信号(见表1)。

表1 实验样本

将实测值代入求得规范化多项式拟合后的表达式为(拟合曲线见图3):

由多项式拟合的6个温度点的对应输出电压为:

由图3中拟合曲线和表2数据可以看出，规范化多项式拟合方法拟合出的数据与实测值非常吻合、精度很高，补偿效果较好。

图3 多项式拟合曲线

表2 拟合数据的比较

3 结论

采用在桥臂上串、并联合适大小电阻的硬件补偿方法主要存在电路复杂、调试困难、准确度低、成本高昂等不足，而且不利于工程应用。而采用基于规范化多项式拟合算法的软件补偿不仅补偿效果好，而且成本较低，易于工程实际应用;除此之外，该补偿方法的精度还跟非线性函数的光滑程度、变化的起伏大小以及等分点的密集度有关。等分点分布越密，精度就越高，同时阶数越高的规范化矩阵，求逆矩阵也越繁琐，可通过分段拟合的方法从而降低矩阵的阶数。

［1］郁有文，常健，程继红.传感器原理及工程应用［M］.西安:西安电子科技大学出版社，2008:51-53.

［2］关 玲，吴 方.一种压力传感器零位漂移的补偿方法［J］.北京:航空计测技术，2000:20(3):20.

［3］袁希光.传感器技术手册［M］.北京:国防工业出版社，1986，451-456.

［4］李科杰.新编传感器技术手册［M］.北京:国防工业出版社，2002:520-521.

［5］孙以材，陈志永，王静.传感器与固体电子学中非线性函数多项式拟合的规范化［J］.电子器件，2004，27(1):1-4.