直流微网孤岛运行状态电压稳定性分析

王碧芳 ，曹 艳

(武汉职业技术学院，湖北 武汉430074)

0 引言

微网作为一种新型电网形式，可以工作于孤岛和并网两种运行模式［1-2］。直流微电网与交流微电网相比，拥有其独特的优点。直流微电网的提出可以简化微电网的控制策略和方法，有效地提高供电的可靠性和稳定性［3］。

在直流微电网系统中不考虑无功功率的流动，电压成为了反映系统功率平衡的唯一指标［4］，因此，母线电压的调节是十分必要的。文献［5］详细介绍了处于不同情况下直流微网内部各变流器工作状态的变化和母线电压参考值的确定。文献［6］提出了一种结合模糊控制和增益调整控制的新型电压控制方法，用于孤岛状态下储能系统对直流母线电压的控制，使得直流电压控制和储存能量的平衡控制可以同时实现。文献［7］根据潮流方程解的存在性推导了一种微网静态电压稳定判别法，并利用其研究了DG的类型、位置对微网电压稳定性的影响。文献［8］采用状态空间法建立了直流微网中多种变流装置的平均模型，并进行了小扰动稳定分析。

1 直流微网架构及建模

1.1 直流微网架构

本文研究的直流微网系统，是将各种负载和电源通过一种功率模块连接到同一直流总线上，如图1所示。

图1 直流微网系统结构

这里将不同操作模式的模块归结于两类:一类为设备配置模式，在这种操作模式下，设备电压和电流被控制;二类为总线配置模式，在这种操作模式下，总线电压通过下垂调控机制控制［9］。

本文将直流微网系统做如下等效，所有设备配置模块侧可以等效为一个功率负载Pbus，而所有总线配置模块侧则等效为一个戴维宁等效源，由此可得其等效电路如图2所示。通过软件配置模块的Rdroop，i和Uref，从而使系统的运行更加灵活。

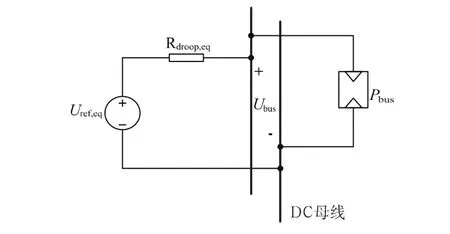
图2 直流微网系统等效电路

1.2 设备配置运行的反馈控制设计

1.2.1 内部电流环设计

一个简单的比例积分(PI)控制器Gi(s)可用于内环，它在期望的交叉频率下实现良好的稳定裕度，保证模块之间的变化分量值不会对性能产生不利的影响。

相对于其他解决方案，这里只需要一个固定的补偿器就足够了。

1.2.2 外环设计

外环反馈设计可以采用小信号等效电路实现，如图3所示。图中电感看作一个受控电流源。当母线电压小于设备电压时，电流调节模式下输出电流iRC的控制需要一个感应信号的修正。

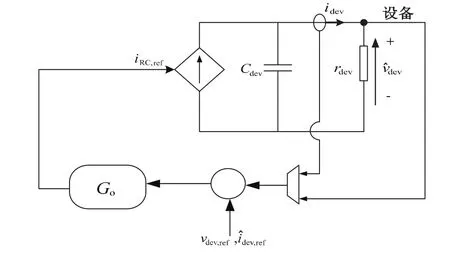
图3 设计外环补偿器的等效小信号电路

因此，送到外环数字补偿器的信号iRC定义为:

式中，di是低通滤波器的占空比。

另外，一阶系统可以很容易地由简单的比例积分补偿器控制:

值得注意的是，两个不同的补偿器独立设计，一个用于设备电流的控制，另一个用于设备电压的控制。

1.3 总线配置运行的反馈控制设计

总线电压用下垂控制法调节，外回路补偿器Gdroop的设计要满足双重目标:保证系统的下垂功能和整个系统的稳定运行。图4为总线配置模块的总线端口的小信号等效电路。

图4 总线配置模块的端口等效电路

总线配置模块的输出阻抗Zo(s)可以用图5算出:

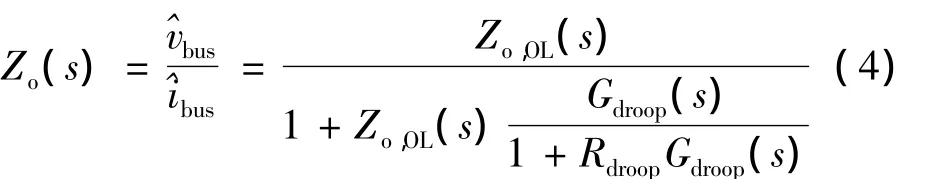
式中，Zo，OL(s)是开环输出阻抗。如果下垂补偿器提供了一个很大的直流增益，Zo(s)的直流特性就是:

公式(5)表明，只要Gdroop(s)满足上述条件，下垂控制可正确实现。

设计Gdroop(s)的方法有很多种，这里使用一个简单的PI补偿器即可。

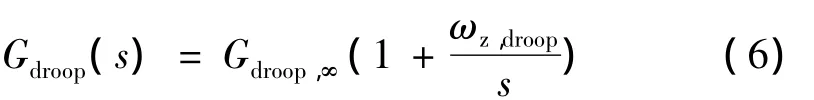
另外，当需要满足特定应用配置时，可以通过设定合适的Uref和Rdroop的值，来调整多个总线配置模块之间的功率分配。

2 孤岛直流微网电压稳定分析

直流微电网的电压稳定可以定义为:当系统受到干扰时，将直流母线电压保持在一定范围内(电压波动不超过额定值的±5%)的能力。本文直流微网系统的稳定性分析是基于阻抗比判据［13］:电源子系统的阻抗对负载阻抗的比例Zsource/Zload变成一个可以利用Nyquist稳定性判据分析的等效回路增益。阻抗比判据有一个大的优点，它可以基于每个子系统的输入输出特性(阻抗)来分析整个系统，而不用分析子系统具体的内部特性。

由图5可以得到所有总线配置模块的戴维南电路如下:

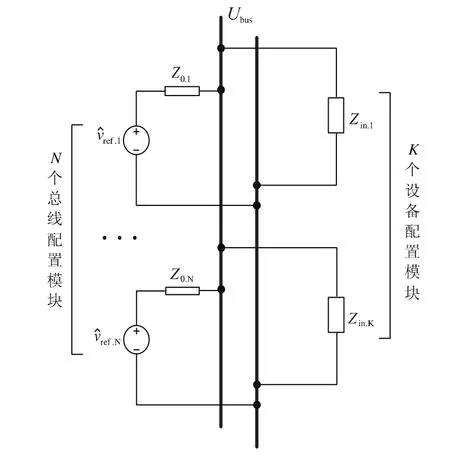
图5 直流微网系统等效电路

所有设备配置模块的等效输入阻抗为:

因此总线电压可以表示为:

用于稳定性分析的等效回路增益可定义为:

式(11)是电源阻抗对负载阻抗比例的形式。一旦所有的阻抗已知，就可以分析总线电压的稳定性。

根据式(4)，其中总线配置模块的输出阻抗仅Rdroop值不同。因此，最坏情况下的输出阻抗可以表示为:

设备配置模块的输入阻抗的不同仅在于Rin值不同，而这又取决于电力需求。因此，最坏情况下的输入阻抗可以表示为:

这里为了分析方便，用ωz，droop和无量纲参数Kdroop表示用PI补偿器设计的Gdroop(s)如下:

图6显示了在一系列不同的ωz，droop和Kdroop值下，Tdroop(s)的恒定相位裕度的等高线图，其中 Cbus=1 mF，Ubus，min=200 V，Pbus，max=50 kW，N=K，则 Rin=－0.8 Ω。图 6(a)中 Rdroop，max=0.3 Ω，而图 6(b)中Rdroop，max=0.6 Ω。比较(a)和(b)图可以得出，0 以下的区域为不稳定区域。Rdroop，max离 Rin，min越近，不稳定区就越大。此外，低值的ωz，droop和较小的Kdroop会引起输出阻抗的剧烈增加，从而降低相位裕度。

考虑模块数的影响，用于稳定性分析的等效回路增益为:

图7(a)是当 Rdroop，max=0.3 Ω和几个大于0.3 Ω值的情况下，而Gdroop(s)为稳定运行设计的某定值时Tdroop(s)的Nyquist图。可以看出，Rdroop越大，系统越不稳定，正如图7所预期的。如果在总线配置模块中编程的Rdroop值高于期望的最大值，这种情况就可能发生。

最后，注意在之前的所有推导中都假设K=N。图7(b)显示了在稳定设计下的Tdroop(s)，Tdroop(s)是比例K/N的函数。如果N＞K，等效输出阻抗变小且相位裕度增加。虽然K＞N不应该在正常运作下发生，但它可应用在过载情况下。

图6 函数Tdroop的恒定相位裕度等高线图

3 MATLAB仿真分析

根据上文得出的结论，对直流总线电压的稳定进行了时域仿真。直流微网的等效模型采用图2，在MATLAB/Simulink中进行仿真分析。其中DC/DC变换器采用Buck电路，负载为恒功率负载。负载采用双环控制，电压外环和电流内环均为PI控制。

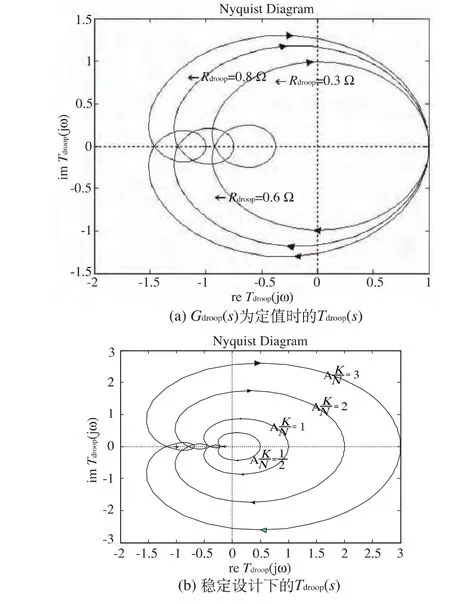
图7 函数 Tdroop(jω)的 Nyquist图

总线电压的仿真波形如图8所示。

图8 总线电压仿真波形

图8(a)中，当 0 ＜ t＜0.4 s时，Rdroop=0.4 Ω，0.4 s＜t＜ 0.8 s时，Rdroop=0.45 Ω。总线电压由24 V突变为22 V，电压变化比为8.3%，系统电压稳定。

图9(a)中，当 0 ＜ t＜0.4 s时，Rdroop=0.4 Ω，0.4 s＜t＜0.8 s时，Rdroop=0.6 Ω。总线电压由24 V突变为13.6 V，电压变化比为43%，系统电压不稳定。

因此，Rdroop越大，系统直流母线电压越不稳定。且仿真结果与图7结果一致。

4 结论

对于直流微电网来讲，由于直流系统的互联只存在电压的大小问题，直流微电网内只需设置一根或者多根直流母线，分布式电源可通过电力变换设备与直流母线相连，同时也减少了控制难度和投资成本。本文研究的是一种基于相同软件配置的电源模块的直流微网系统，可以处理不同的电源和负载间的相互作用。整个系统的稳定性是用阻抗比准则分析的，并设计了一个下垂补偿器保障系统的稳定性。仿真结果表明了直流微网母线电压稳定性与各参数之间的关系。其中Rdroop越大，系统越不稳定。且 Rdroop，max离 Rih，min越近，不稳定区就越大。

［1］Lasseter R H.Microgrids［C］.Power Engineering Society Winter Meeting.New York，USA:IEEE，2002:305-308.

［2］鲁宗相，王彩霞，闵 勇，等.微电网研究综述［J］.电力系统自动化，2007，31(19):100-107.

［3］岳飞飞.直流微电网的能量管理研究［D］.秦皇岛:燕山大学，2012.

［4］施 婕，郑漳华，艾 芊.直流微电网建模与稳定性分析［J］.电力自动化设备，2010，30(2):86-90.

［5］AZAROIU G C，POPESCU M O，DUMBRAVA V，et al.Voitage control system and transient analysis of DG interfaced dc distribution svstem［C］.IET Conference on Renewable Power Generation，Edinburgh，UK，2011:1-6.

［6］KAKIGANO H，NISHINO A，ISE T.Distribution voltage control for DC microgrid with fuzzy control and gain-scheduling control［C］.8th International Conference on Power E-1ectronics，Jeiu，South Korea，2011:256-263.

［7］Katiraei F，Iravani M R.Power management strategies for a microgrid with multiple distributed generation units［J］.IEEE Trans on Power Systems，2006，21(4):1821-1831.

［8］Miguel Rodr'iguez，Stahl G.Smart DC Power Management System Based on Software-Configurable Power Modules［J］.IEEE Transactions On Power Electronics，2013，28(4):1571-1586.

［9］Rodriguez M，Olalla C，Corradini L，Maksimovic D.Average current-mode control of boost converters with bidirectional power transfer capabilities［J］.in Proc.13th IEEE Workshop Control Model.Power Electron.，2012，(6):1-7.

［10］Wong P L，Lee F，Xu P，Yao K.Critical inductance in voltage regulator modules［J］.IEEE Trans.Power Electron.，2002，17(4):485 492.

［11］Stahl G，Rodriguez M，Maksimovic D.A high-efficiency bidirectional buck-boost dc-dc converter［C］.in Proc.27th Ann.IEEE Appl. Power Electron. Conf. Expo.， Feb.2012:1362-1367.

［12］Ridley R，Cho B，Lee F.Analysis and interpretation of loop gains of multiloop-controlled switching regulators［J］.IEEE Trans.Power Electron，1988，3(4):489-498.

［13］Ahmadi R，Paschedag D，Ferdowsi M.Closed-loop input and output impedances of dc-dc switching converters operating in voltage and current mode control［C］.inProc.36th Ann.Conf.IEEE Ind.Electron.Soc.，Nov.2010:2311-2316.