一种基于预测开路电压估算SOC初值的方法
龙宇舟,郭毅锋,韩峻峰,潘盛辉
(广西科技大学电气与信息工程学院,广西柳州545006)
0 引言
估算电动汽车动力电池SOC是电池管理系统的核心内容之一,SOC估算方法多种多样,其中的很多估算方法需要以SOC初值为基础,例如,安时法、卡尔曼滤波法等。实际生活中,电动汽车的正常使用必然存在长时间停车,然后再重新启动进入驾驶模式的情形。每一次重新启动都伴随着一个新的SOC初值,本文针对电动汽车重新启动时刻的SOC初值,提出了一种新的估算方法。
对于SOC初值的确定,目前国内最常用的有两种方法:第一种利用开路电压与SOC函数关系式估算SOC初值;第二种对电池端电压进行迭代运算求得SOC 初值[1,2]。
本文提出了一种新的SOC初值估算方法,不需要测量电池的开路电压,也不需要进行迭代运算,只需要知道电动汽车动力电池停车初始时刻端电压,便可精确地估算出SOC初值。
1 预测开路电压原理与设计
1.1 电池模型及参数辨识
电池存在时变特性,在进行电池参数辨识和状态估计时,需要建立电池模型。电池常用的模型有:电化学模型、热模型和等效电路模型等。其中,等效模型具有简单、直观、易于建立等优点,所以被广泛应用于电池相关研究中[3,4]。本文选取的模型为Thevenin等效模型,如图1所示。
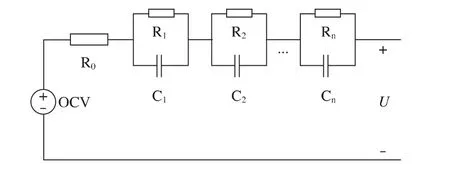
图1 Thevenin等效模型
图1中,OCV为电池开路电压,R0为欧姆内阻,Rn为极化内阻,Cn为极化电容,U为电池端电压,n代表极化部分的阶数。
按本文提出的方法估算SOC初值,结果如表1所示。
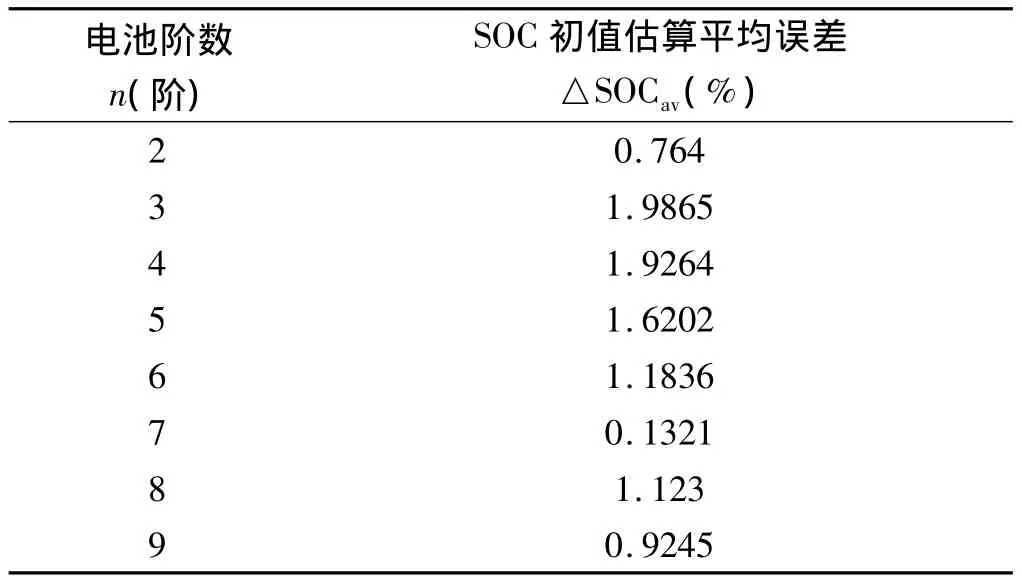
表1 SOC初值估算平均误差
从表1可见n=7时,SOC初值的估计最准确,所以文章采用的等效电池模型为七阶,即n=7。根据基尔霍夫定律,电池放电的端电压为:

式中,I为放电电流;U01…U07;τ1…τ7为待定系数。
在参数辨识领域中,最小二乘法是一种基本的估计方法。该方法的特点有:(1)它既可用于动态系统亦可用于静态系统;(2)既可用于线性系统亦可用于非线性系统;(3)既可用于离线估计又可用于在线估计;(4)在随机环境下,利用最小二乘法时,并不要求观测数据提供出有关它的概率统计方面的信息,而这种方法获得的估计结果却有相当好的统计特性[5,6]。
七阶Thevenin等效电池模型是非线性的动态系统,因此最小二乘法适合该模型的参数辨识。
对锂离子动力电池脉冲放电曲线,利用最小二乘法曲线拟合函数lsqcurvefit[7]进行曲线拟合并辨识U01…U07,τ1…τ7待定系数,曲线拟合结果如图2所示。
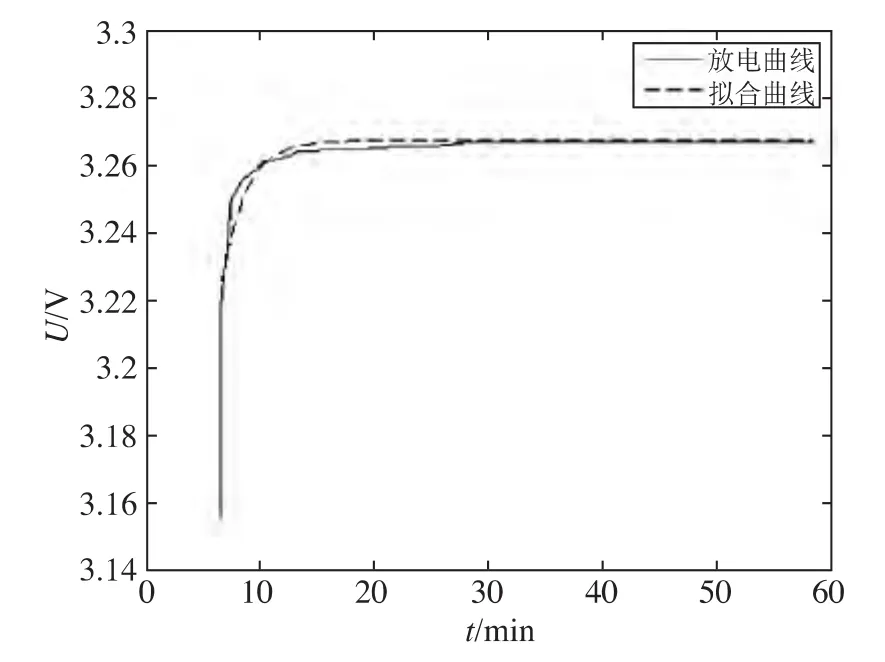
图2 电池脉冲放电曲线拟合图
通过图2可见,拟合曲线与实际放电曲线十分接近,在拟合末期电压误差值小于0.001 V。因为文章所取预测开路电压只与拟合曲线末时刻的电压值有关,0.001 V的误差对SOC初值估计影响小,可忽略不计,所以本文辨识参数的方法合适。
1.2 脉冲放电实验
在不考虑锂离子动力电池温度变化影响电池特性的情况下,假设电动汽车进行“匀速行驶-停车-匀速行驶-停车”循环驾驶模式。因为匀速行驶可视为电池恒流放电情形,停车视为电池静置情形。所以,可以用锂离子动力电池脉冲放电实验模拟“匀速行驶-停车-匀速行驶-停车”情形[8,9]。
实验内容:在外界温度为20℃情况下,对额定容量10 Ah、额定电压为3.2 V的磷酸铁锂电池,以1C放电倍率、55分钟为周期进行脉冲放电实验。其中,放电时间为6分钟,代表电动汽车匀速行驶时间6分钟。静置时间为49分钟,代表电动汽车停车时间49分钟。
在6分钟放电过程中,电池SOC将下降10%。在49分钟静置过程中,电池内部化学反应达到平衡,电池端电压由于回弹特性得到一定程度上升,最终达到稳定值,并且将最终的稳定值看作电池的开路电压OCV。
锂离子动力电池,从SOC为100%到0%进行脉冲放电实验,因为每一次脉冲放电实验 SOC下降10%,所以整个脉冲放电实验正好进行10次,即模拟了10次匀速驾驶-停车情形,如图3所示。
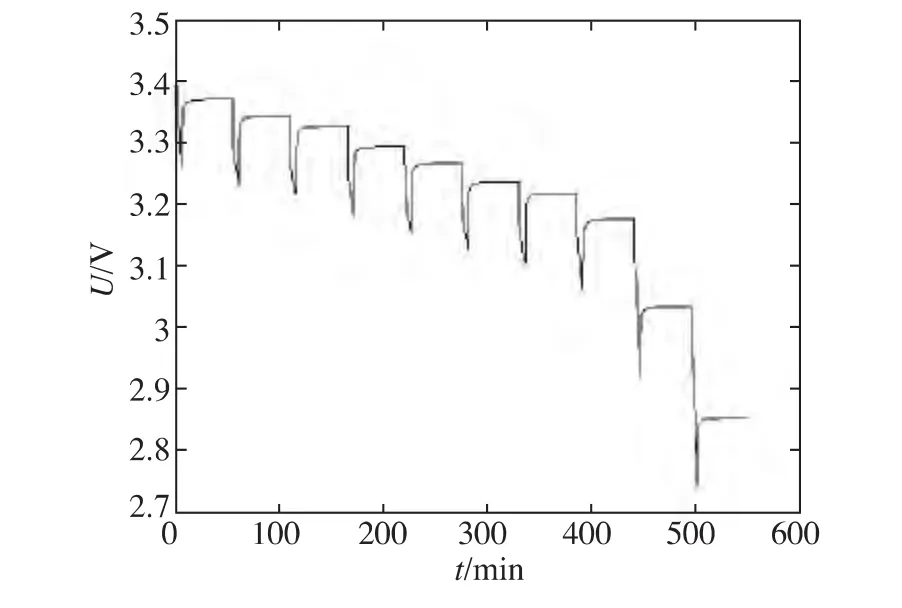
图3 脉冲放电实验
因为每次SOC下降10%,所以锂离子动力电池在静置的末时刻SOC值分别为90%、80%、…0。在静置的末时刻电池的端电压达到稳定,可将其当做锂离子动力电池的开路电压OCV。利用Matlab将10组SOC和OCV值拟合成OCV-SOC函数关系式:

1.3 预测开路电压方法
图4为SOC从60%下降到50%的脉冲放电曲线,从图4可见电池端电压的变化呈现两段的情形。第一段,因为欧姆内阻的作用电池端电压会在电流加载或撤除的瞬间出现跳跃式变化;第二段,因为极化部分的作用电池端电压随着电流的加载或撤除缓慢变化[10]。
因此通过七阶Thevenin等效模型,可写出锂离子动力电池静置阶段的开路电压为:
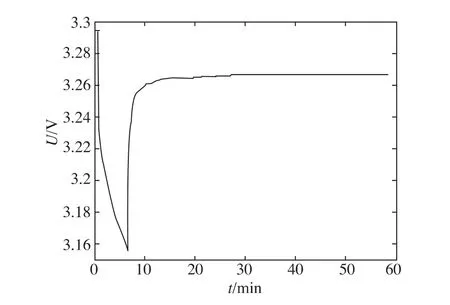
图4 SOC从60%下降到50%脉冲放电

式中,U(t0)为静置初始时刻电池的端电压,其值可以通过电池端电压采集系统取得。
设锂离子动力电池静置从开始至结束,由电池的回弹特性使电池端电压从U(t0)上升到OCV的电压变化量为△U:

整个脉冲放电实验进行了10次,因此利用七阶Thevenin等效模型辨识的参数,可以求出10次脉冲放电实验的电压变化量△U,结果如表2所示。

表2 电压变化量
由表2可见每一次脉冲放电实验的电压变化量△U不同,并且彼此相差不大。所以考虑用一个平均电压变化量△Uav来替代所有的△U,设△Uav:
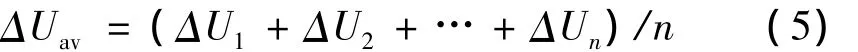
将公式(5)替代公式(4),然后代入公式(3)有:
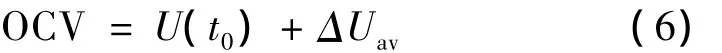
预测开路电压思路:①利用最小二乘法拟合曲线时辨识的参数求出七阶Thevenin等效模型的电压变化量△U。②利用求出的电压变化量△U,按公式(5)求取电压平均变化量△Uav。③结合静置初始时刻的电池端电压U(t0),利用公式(6)估算出开路电压OCV。
经过公式(3)、(4)、(5)、(6)的推导,可求出预测的开路电压OCVy:
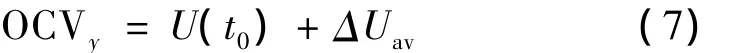
结论:按此方法,电动汽车便可以在无需测量动力电池OCV的情况下,直接预测出电动汽车重新启动时刻的开路电压。
2 SOC初值估算实验及结果分析
电动汽车停车后,电池本身存在一个自放电,其中锂离子动力电池的自放电率为10%(一个月),即电池静置一个月,电池电量流失10%。本文不考虑电动汽车停车一个月及更长时间的情况。电池短时间自放电流失的电量极少,在估算SOC初值时,忽略不计。
脉冲放电实验进行了10次,即模拟了10次匀速驾驶-停车情形,每一次实验测量得到一个开路电压值OCV,同时针对10次的脉冲放电实验,按照文章预测开路电压的方法,分别预测10次的开路电压OCVy。然后,分别将 10次的 OCV和 OCVy代入 SOC=f(OCV)函数关系式,求得10次模拟匀速驾驶-停车情形的SOC初值,设为SOCocv、SOCocvy。最后,将初值结果SOCocv、SOCocvy进行比较,求出SOC初值估计的绝对误差△SOC和平均误差△SOCav,结果如表3所示。
设绝对误差为:

平均误差为:


表3 SOC初值估算结果
SOC初值估算的平均误差:

通过表3,可以看出预测的开路电压OCVy估算的SOC初值SOCocvy与实际测量的开路电压OCV估算的SOC初值SOCocv绝对误差相当小,平均误差也只有0.1321%。
市场上通用的电池容量测试仪的精度一般在0.5% ~3%之间不等,本文SOC初值的估算精度高于市场上通用的电池容量测试仪精度,因此文章提出的方法具有可行性。
3 结论
本文以锂离子动力电池为对象,针对电动汽车匀速驾驶-停车情形,采用了七阶Thevenin等效电池模型,进行了开路电压的预测,估算了SOC初值。其估算精度高于市场上通用的电池容量检测仪精度,证明了文章提出的方法具有可行性,为电动汽车SOC初值的估算提供了一种新方法。在不考虑温度对电池影响的情形下,仅对锂离子电池进行了SOC初值估算。因此,温度的影响与其它类型电池SOC初值的估算将是下一步工作的重点。
[1]华周发,李 静.电动汽车动力电池SOC估算方法综述[J].电源技术,2013,37(9):1686-1689.
[2]李 超.电动汽车用镍氢电池模型参数辨识和SOC估算研究[D].天津:天津大学,2007.
[3]郭毅锋.铅酸动力电池等效电路模型参数辨识方法研究[J].科学技术与工程,2012,12(17):4165-4169.
[4]张彦琴,郭 凯,刘汉雨.铅酸电池模型及参数辨识研究[J].蓄电池,2013,50(3):140-144.
[5]汪秋婷,肖 铎,金 晖.基于抗差UKF的动力锂电池SOC估计算法研究[J].电源技术,2013,137(8):1388-1392.
[6]孙传余,肖林京,于志豪,等.基于最小二乘法的磷酸铁锂电池 SOC 估计[J].山东科技大学学报,2013,32(2):94-101.
[7]景振毅,张泽兵,董 霖.Matlab 7.0实用宝典[M].北京:中国铁道出版社,2008.
[8]徐欣歌,杨 松,李艳芳,陈文芗.一种基于预测开路电压的SOC估算方法[J].电子设计工程,2011,19(14):127-129.
[9]魏学哲,孙泽昌,田佳卿.锂离子动力电池参数辨识与状态估计[J].同济大学学报,2008,36(2):231-235.
[10]HU Xiao-song,SUN Feng-chun,CHENG Xi-ming.Fuzzy Model for Estimation of the State-of-Charge of Lithium-Ion Batteries for Electric Vehicles[J].北京理工大学学报(英文版),2010,19(4):416-421.

