考虑缺货成本的三级供应链收益共享契约研究
曹庆奎,商娜欣,李小波
(1.河北工程大学 经济管理学院,河北 邯郸 056038;2.长安大学 经济与管理学院,陕西 西安 710064)
供应链收益共享契约(Revenue-sharing contract)是在制造商、供应商和零售商之间建立的一种交易模式,供应商提供较低的批发价格给零售商,按照一定的收益共享比例将收益的一部分与供应商进行分享,通过收益共享契约,零售商可以降低自身的库存风险[1],由于从供应商得到商品的批发价格较低,零售商能保证自己的收益水平,从而促进零售商加大库存从供应商处订购更多的商品,供应商就会需要更多的商品,从而刺激制造商的生产量,供应链整体的运作效率和整体收益都会有一定程度的增加[2]。根据Warren和Peers[3]的调查和研究,美国著名的录像带租赁公司Blockbuster在1998年最先引入收益共享契约进行业务的协调和管理,采用收益共享契约后,公司的业绩大大提高,市场份额由25%上升到31%,效益由24%增加到40%[4],可以看出,收益共享契约是供应链协调的有效手段。关于供应链收益共享契约的研究,李绩才等(2013)[1]研究了一个供应商多个零售商的两级供应链,假设多个零售商之间存在竞争关系,目标函数为期望效用最大化,分析了在不同收益共享比例下的供应链的协调机制。刘玉霜和张继会(2013)[5]研究了由一个制造商与两个竞争零售商组成的两级供应链系统的最优决策及契约协调问题。徐广业等(2011)[6]研究了在需求具有价格敏感性条件下双渠道供应链中的两种协调方式,即传统分销渠道与电子直销渠道之间的协调及上下游节点之间的协调。常佳佳和胡支军(2012)[7]假设在竞争环境下的两级供应链协调问题,研究了在季节性商品的销售过程中预先订购折扣合约在供应链协调中的应用。本文在考虑存在缺货成本的情况下,对三级供应链的收益共享契约进行研究。
1 问题描述及模型假设
本文以由一个制造商、一个分销商、一个零售商组成的三级供应链系统为主,假设市场需求为随机需求,商品的零售价格与市场需求相关,并且考虑商品的缺货损失成本情况下的收益共享契约问题, 并且进一步研究了在这种假设下收益共享契约协调供应链的过程,三级供应链的决策过程如图1所示。

在本文中,p表示零售商的商品零售价格,q表示零售商的商品订货量;w1表示制造商给分销商的单位商品批发价格;w2表示分销商给零售商的单位商品批发价格;c表示除批发价格外的订购生产成本;h代表缺货成本;v表示商品剩余成本;s表示零售商的预期商品销售量;s1表示零售商的商品剩余量期望值;s2表示零售商的商品缺货量期望值;π表示供应链的利润;用下标m、d、r分别表示制造商、分销商以及零售商。其他符号及说明如下:
ε:非负的连续的均值为1的随机变量;
x:具有价格弹性的市场随机需求;需求与价格有关,采用加和形式,设x=y(p)+ε,y(p)为零售价格的减函数;
F(ε):市场随机需求的分布函数,设其为连续、可微可逆;
f(ε):市场随机需求的密度函数;当ε>0时,F(ε)>0,f(ε)>0;
φ1:制造商与分销商之间的收益共享参数,设分销商获得的比例为φ1,制造商获得的比例为1-φ1,0<φ1≤1;
φ2:分销商与零售商之间的收益共享参数,设销售商获得的比例为φ2,制造商获得的比例为1-φ2,0<φ2≤1;
2 集中决策下三级供应链决策
在集中决策的情况下,供应链是一个决策整体,假设是制造商、分销商和零售商同属于一家企业,并且都为风险中性的,集中决策时制造商由于规模较大,生产情况、市场需求以及各成员的风险态度等信息都是共享的,制造商能够从这些信息中推测出零售商的最优订购量,从而提前组织生产与最优订购量相同的产品,也就是说在集中决策时,制造商、分销商和零售商是一个利益完全一致的整体,供应链整体可以合理安排生产以及销售资源,从而使整个供应链的期望利润最大化。
根据供应链利润公式,可得集中决策下供应链的整体期望利润为:
E[π(p,q)]=ps+vs1-cq-hs2
(1)
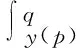
(2)
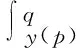
(3)
s2=y(p)+E(ε)-s=y(p)+E(ε)-q+

(4)
设d=y(p)+E(ε),则s2=d-s=d-q+

(5)
(6)

3 收益共享契约下三级供应链决策
3.1 零售商决策模型
在分散决策情况下,零售商根据分销商给出的收益共享比例φ2以及零售价格w2选择订货量,在与分销商缔结了收益共享契约的条件下,分散决策时零售商从自身角度出发,最优决策是使自身的期望利润最大化[8],零售商的期望利润为:
E[πr(p,q,φ2)]=φ2(ps+vrs1-hrs2)-(w2+cr)q
(7)
对期望利润求一阶导数,并令导数为0,可得零售商的商品最优订货量qr*:
(8)
分散决策下,供应链协调运作时必须满足qr*=q*,计算可得供应链协调运作下零售商收益共享系数φ2以及零售商批发价格w2满足的关系式:
(9)
3.2 分销商决策模型
分销商在收益共享契约下,根据与制造商之间制定的收益共享系数φ1以及与零售商之间制定的收益共享系数1-φ2的条件下,为了达到供应链的整体协调,分销商的订购量与零售商相同,都为q,分散决策下,分销商的决策目标是自身的期望利润最大化,分销商的期望利润为:
E[πd(p,q,φ1,φ2)]=φ1[(1-φ2)(ps+vrs1-hrs2)+w2q-hds2]-(w1+cd)q
(10)
对期望利润求一阶导数,并令导数为0,可得分销商的商品最优订货量qd*:
(11)
分散决策下,供应链协调运作时必须满足qd*=q*,计算可得供应链协调运作下分销商与零售商之间的收益共享系数φ2、分销商以及制造商之间的收益共享系数φ1以及分销商批发价格w2满足的关系式:
(12)
3.3 制造商决策模型
在三级供应链中,制造商规模较大,是行业的领导者,在制定最优决策时,从自身角度出发,也以期望利润最大化为决策目标[9],因此制造商的期望利润为:
E[πm(p,q,φ1,φ2)]=(1-φ1)[(1-φ2)(ps+vrs1-hrs2)+w2q-hds2]+(w1-cm)q-hms2
(13)
供应链在达到协调运作时,制造商确定的最优价格p*应满足以下条件,
(14)
4 收益共享契约下三级供应链协调机制分析
三级供应链协调的情况下,并且收益共享系数满足0<φ1≤1,0<φ2≤1,w1>0,w2>0的条件下,可以求出收益共享系数可以使三级供应链达到协调时候的取值范围,
(15)
根据上文公式可以求出供应链达到协调时制造商分销商和零售商的利润函数分别为:
(16)
由上式可以看出,不同的收益共享系数决定了制造商分销商以及零售商之间的收益水平,通过调节收益共享系数可以有效的调节制造商以及分销商之间的批发价格,分销商以及零售商的批发价格,从而使整个供应链达到协调。
5 算例分析
假定市场需求服从均匀分布,密度函数为:

(17)
市场需求量函数为:
x=y(p)+ε=bp-k+ε(b>0,k≥1)
(18)
其他参数和假设值见表1。

表1 参数及假设值
将参数假设值代入上文公式中,可计算出最优生产量以及最优价格组合(20,1 000),可得φ1和φ2能使供应链协调的取值范围为0.5<φ1≤1,0.2<φ2≤1,根据φ1和φ2的不同值,可以计算出供应链在不同的收益共享参数组合下的供应链成员的利润,见表2。

表2 不同收益共享系数下供应链成员期望利润
从表2中可以看出,当收益共享系数组合为(1,1)时,供应链是不协调的。假设φ1不变,零售商的期望利润值随着φ2的增大而增大;假设φ2不变,分销商的期望利润随着φ1的增大而增大;假设φ1不变,分销商的期望利润随着φ2的增大而而减小;假设φ2不变,制造商的期望利润随着φ1的增大而减小。
6 结语
收益共享契约可以使三级供应链达到协调,供应链成员的利润都与收益共享系数的大小有关,并且不同的收益共享系数可以有效协调利润在制造商、分销商以及零售商之间的分配,并且在供应链达到协调的情况下,存在着不同的收益共享系数组合,实行什么样的收益共享系数组合取决于三级供应链成员各自的协调能力。
参考文献:
[1] 李绩才,周永务,肖 丹,等.考虑损失厌恶一对多型供应链的收益共享契约[J].管理科学学报, 2013, 16 (2): 72-82.
[2] 蔡建湖.不确定环境下的供应链管理[M].北京:科学出版社, 2011.
[3] WARREN A, PEERS M. Video retailers have day in court: Plaintiffs say supply deals between Blockbuster Inc. and studios violate laws [N]. Wall Street Journal, 2002- 6-13(B10).
[4] MORTIMER J H. Vertical contracts in the video rental industry [J]. Review of Economic Studies, 2008, 75(1):165-199.
[5] 刘玉霜, 张纪会.零售商价格竞争下的最优决策与收益共享契约[J].控制与决策, 2013, 28(2): 269-278.
[6] 徐广业, 但 斌, 肖 剑.基于改进收益共享契约的双渠道供应链协调研究[J].中国管理科学, 2010, 18(6):59-63.
[7] 常佳佳,胡支军.竞争环境下多个损失规避零售商的预先订购折扣合约研究[J].经济数学,2012,29(2):11-16.
[8] 费 威. 供应商与零售商的策略机制分析[J]. 河北科技大学学报, 2012, 33(3): 221-225.
[9] 李巍巍, 吴 冲. 基于Shapley值法和直觉模糊的煤炭供应链利益分配[J]. 黑龙江科技学院学报, 2010, 20(6): 483-487.

