弹性索参数对三塔悬索桥抗震性能影响研究

闫聚考，李建中，彭天波

(同济大学 土木工程防灾国家重点实验室,上海 200092)

三塔悬索桥可实现连续长大跨越, 突破单一跨径的限制, 是跨越宽广水域的可行方案。国外方案竞赛中曾多次提出大跨三塔或多塔悬索桥方案, 但至今没有建成的实例[1-3]。2012年底，中国建成了第一座大跨三塔悬索桥，实现了超千米级三塔悬索桥连续跨越。缆索支承桥梁的塔、梁、墩之间的连接方式对桥梁的静、动力性能有很大的影响。桥塔的受力很大程度上取决于塔、梁之间的连接方式，如果塔与梁体间采用固结，在地震作用下的梁端位移很小，但会在塔引起较大的地震力，而竖向支承体系(采用纵桥向滑动支座)可以看成是隔震体系，在地震作用下，可以减小塔柱的内力反应，但会导致相当大的位移。控制梁端位移的措施主要有在塔、梁间设弹性连接装置或阻尼器等, 国内外已有一些桥梁设置了此类装置。例如，日本多多罗斜拉桥在塔、梁间设置了大型橡胶支座[4]，广东汕头海湾二桥、日本名港中大桥在塔、梁间设纵向钢铰线拉索[5]。叶爱君等[6]分析了弹性连接装置与粘滞阻尼器对某斜拉桥地震位移的影响。Tony S Vader 等[7]研究了摩擦阻尼器和非线性粘滞阻尼器对旧金山奥克兰海湾大桥的减震效果。聂利英等[8]以西堠门大桥为背景，从抗震角度对梁端自由、梁端设置粘滞阻尼器以及设置锁定装置3种梁端约束体系下的性能进行比较分析，最终选定设置粘滞阻尼器。Hosam-eddin等[9]研究了橡胶支座和铅芯橡胶支座等减震装置对斜拉桥抗震性能的影响。本文以泰州长江公路大桥为背景，用反应谱方法，分析了弹性索参数对大跨三塔两跨悬索桥抗震性能的影响。

1 工程背景

泰州长江公路大桥工程位于江苏省境内长江中段，上距润扬长江公路大桥60 km，下距江阴长江大桥60 km，北接泰州市，南联镇江市和扬州市。泰州长江公路大桥主跨为三塔悬索桥，两个主跨的跨度均为1 080 m，主缆的分跨为390+1 080+1 080+390 m。主航道桥起止桩号K14+966.000～K17+906.000，如图1所示。其中，中塔为变截

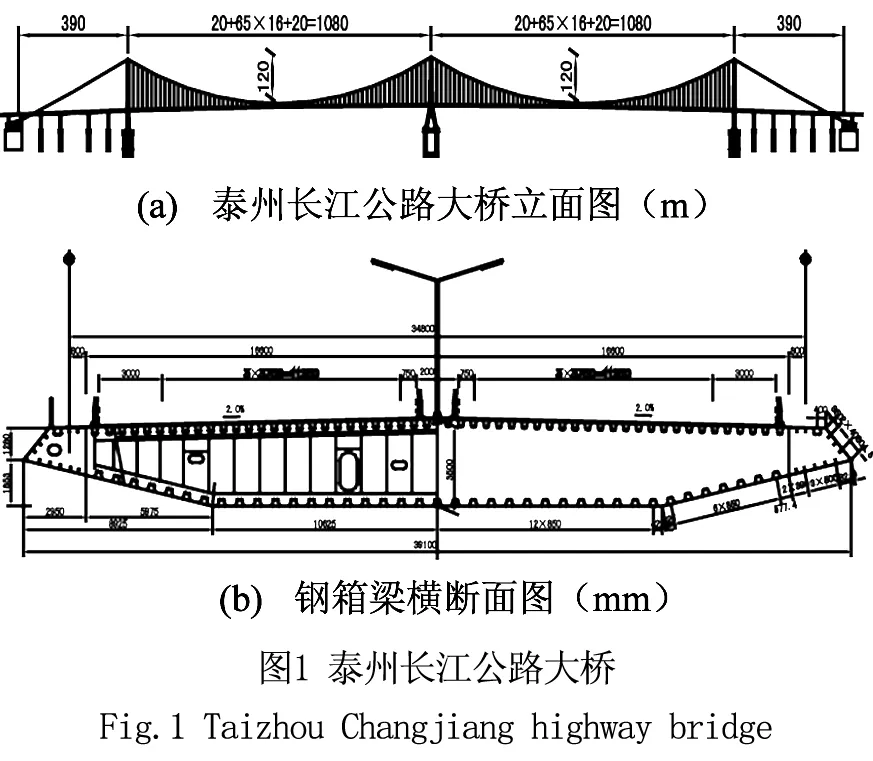
面钢塔，塔高194 m，横桥向为门式框架结构，纵向人字型。叉开处设等截面梯形钢横梁，梁高5 m，上横梁采用横桥向倒K形横梁。边塔包括上塔柱、下塔柱和上下横梁、下横梁，塔柱采用箱形断面，采用C50混凝土。塔柱顶高程180 m。加劲梁采用抗风性能好、整体性强、造型美观的封闭式流线型扁平钢箱梁，加劲梁设上斜腹板及下斜腹板构成导风嘴。中塔下横梁上不设竖向支座，也不设0号吊索，在塔内侧壁与主梁间安装横向抗风支座，限制主梁的横向位移，纵向设弹性索。在边塔下设置竖向和侧向支座。

2 有限元模型

采用脊骨梁模式建立悬索桥空间有限元分析模型，主梁、主塔和墩柱用空间梁单元模拟，主缆、吊杆采用空间杆单元模拟，主缆、主塔和吊杆均考虑恒载引起的几何刚度的影响。对于边塔，由于一般冲刷层位尚在承台底面以上，属于低桩承台基础，采用在承台底中心加6×6的土弹簧来模拟桩土相互作用。而对于中塔，在一般冲刷线处沉井部分也采用空间梁单元进行模拟，采用刚性杆模拟沉井侧边缘与形心处的变形关系，在沉井侧边缘采用弹簧单元模拟一定高度土层与沉井的相互作用，在沉井底面采用弹簧单元模拟一定范围土体与沉井的相互作用。中塔和主梁之间在纵向采用弹性索连接，通过不断改变弹性连接刚度(1×100～1×1010kN/m，共分19级)，进行了一系列地震反应分析。三维有限元模型如图2。

分析时，输入重现期2450年、阻尼比为3%的场地加速度反应谱，对结构进行反应谱分析，取前800阶振型，按CQC法进行组合。地震输入采用纵向+竖向，方向组合采用SRSS方法。竖向加速度反应谱的形状与水平向加速度反应谱一致(即动力放大系数谱相同)，加速度峰值为水平向加速度峰值的2/3，并取三条反应谱结果的平均值。典型的场地反应谱如图3。

3 弹性索参数分析

图4～图9给出了中塔、主梁之间设置纵向弹性连接时，弹性连接刚度对结构地震反应的影响。图4为梁端位移随k的变化曲线，图5为塔顶位移随k的变化曲线，图6为北塔底内力随k的变化曲线，图7为中塔底内力随k的变化曲线，图8为南塔底内力随k的变化曲线，图9为弹性索变形和内力随k的变化曲线。

从图4可以看出，梁端位移随着k的增大开始阶段有所波动，但当k达到2.5×106kN/m后迅速减小并很快趋于稳定。k在2.5×105～7.5×105kN/m之间时，弹性索刚度不太大，又能有效地减小梁端位移。从图5可以看出，边塔(北塔和南塔)塔顶位移随着k的增大开始阶段变化很小，当k在1×105～1×106kN/m之间时，该位移随着k的增大而减小；当k在1×106～1×107kN/m时，该位移随着k的增大而迅速增大并很快趋于稳定。中塔顶位移在开始阶段随着k的增大而减小，但当k大于1×106kN/m时，该位移随着k的增大迅速增加，直到k在1×107kN/m时趋于稳定。

从图7可以看出，随着k的增大，中塔塔底内力反应总体上不断增大。k小于1×105kN/m时，该内力随着k的增大变化很小；当k在1×105～1×106kN/m之间时，该内力随着k的增大迅速增大；当k达到1×108kN/m时，该内力随着k的增大趋于稳定。从图6和图8可以看出，由于结构的对称性，边塔(南塔和北塔)的内力随k的增大有相同的变化规律。边塔底内力随着k的增大开始阶段变化很小；但k在1×105～1×106kN/m之间时，边塔底内力随k的增大而减小；当k在1×106～1×107kN/m之间时，边塔内力随着k的增大而变大；当k大于1×107kN/m时，边塔内力随着k的增大趋于稳定。

从图9可以看出：弹性索变形和内力在开始阶段随k的增大变化很小；当k在1×105～1×107kN/m时，弹性索的位移随k的增大迅速变小，弹性索的内力随k的增大迅速增大；当k大于1×107kN/m时，弹性索位移和内力随着k的增大趋于稳定。

4 结论

1)弹性索k度在2.5×105～7.5×105kN/m范围内取值时，不仅可以减小梁端位移，而且还可以减小主塔的塔顶位移。

2)弹性索k度在1×105～1×106kN/m范围内取值时，可以减小边塔底的内力，而较小程度上增加中塔底的内力。弹性索是一种弹性连接装置，不具备耗能能力，只是改变结构惯性力的传递途径。

3)弹性索k度在2.5×105～7.5×105kN/m范围内取值时，可以有效的减小中塔、主梁间的相对位移(弹性索变形)。

综上，中塔、主梁间弹性索刚度在2.5×105～7.5×105kN/m范围内取值时，可以有效控制梁端位移和中塔、主梁间的相对位移；可以减小边塔内力，而且还可以兼顾中塔的受力。泰州桥施工图中，中塔、梁弹性连接刚度采用6.4×105kN/m，处于合理刚度取值范围内。

参考文献：

[1] FORSBERG T. Multi-span suspension bridges [J].International Journal of Steel Structures, 2001, 1(1):63-73.

[2] GIMSING N J. Cable supported bridges [M]. Chichester: John Wilel & Sons, 2011.

[3] YOSHIDA O, OKUDA M, MORIYA T. Structural characteristics and applicability of four-span suspension bridge[J].Journal of Bridge Engineering,2004,9(5):453-463.

[4] MASASHI Y, TORU F, KAZUO S. Design of Tatara bridge[J]. Engineering Review, 2003，25,(3)：55-62.

[5] MANABU ITO. The cable-stayed Meiko Grand bridges, Nagoya[J]. Structural Engineering International, 1998, 8(3):168-171.

[6] 叶爱君,胡世德,范立础.超大跨度斜拉桥的地震位移控制[J].土木工程学报, 2004, 37( 12) : 38-43.

[7] VADER T S, MCDANIEL C C. Influence of dampers on seismic response of cable-supported bridge towers [J].Journal of Bridge Engineering, 2007, 12(3): 373-379.

[8] 聂利英, 李建中, 胡世德, 等.西堠门大桥3种梁端约束体系比较[J].桥梁建设, 2006(6):73-78.

[9] HOSAM-EDDIN M, AHMED M.ADBEL-GHAFFAR. Seismic energy dissipation for cable-stayed bridges using passive devices[J]. Earthquake Engineering & Structural Dynamics, 1994, 23(8):877-893.