中考数学复习中的分类讨论题型研究

周芳庆

摘 要： 分类讨论的题型在中考数学试题中的比重逐年增加，在中考复习中引起了广大教育工作者的重视.本文从分类解题思想入手，以盐城中考分类讨论题型为例，分析了分类讨论思想在解题过程中的应用，旨在引起广大师生对分类解题思想的重视，提高学生的解题能力.

关键词： 中考数学复习 分类讨论 解题研究

近几年来，在中考数学试题中“分类讨论”的题型逐渐增多.分类讨论试题考察的知识较全面，需要学生有具备缜密的思维逻辑.然而从学生的实际作答情况来看，学生在解决此类问题时还有一定困难，部分学生存在分析不够全面、遗漏答案的问题.因此，在中考复习中加强对分类讨论题型的研究十分必要.

一、把握分类讨论的思想

分类讨论是数学学习过程中常用的一种解题思路与方法，所谓的分类讨论就是指当所给出的数学题目不能采用统一标注化的方式研究与解决时，需要按照某个标准对数学研究对象进行分类，对每一个类型的研究得出相应结论，之后将每个类型的答案进行综合总结，化整为零，逐一解决，最终得出整个数学题目的答案[1].在历年的中考中，分类讨论题型不仅在地中档难度的考题中出现，而且大量出现在高档难度和整个试卷的压轴题中.因此，在中考复习中，教师一定要足够重视分类题型，全面了解分类讨论的解题思想，同时还需要在教学过程和复习环节采取有效的分类解题措施，提高学生对分类解题思想的认识程度，逐步提高学生分类解决数学问题的能力.

二、分类讨论题型的解题研究

（一）根据概念性质分类讨论

分析：这是一个方程式，但是本题条件并没有未指出该方程是关于x的一次方程，还是二次方程，因此可以按照方程的定义进行分类讨论.

（2）当K≠0时，题目中的方程为一元二次方程，此时要想使方程有实根，需要保证△≥0，此时解得k≥-1综合（1）（2）两个结果，可以得出结论：即k≥-1时，方程有实根.

在解答这个问题时，需要正确理解方程有“实根”的含义，由于题目中没有明确指出方程的条件，因而要分两种情况进行考虑与分析.这种以数学概念、定义为标准分类讨论题是中考复习中常见的习题，要给予重视[2].

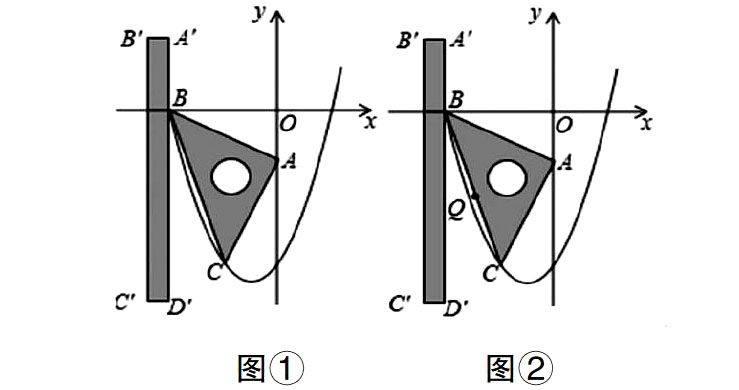
（三）根据不同运动状态分类讨论

（1）求点C的坐标及二次函数的关系式；

（2）若运动过程直尺的边A′D′交边BC于点M，交抛物线于点N，求线段MN长度的最大值；

（3）如果图②设点P为直尺A′D′上的任意一点，连接PA、PB、PC、Q为BC中点，试探究：在直尺平移的过程中，当PQ=时，线段PA、PB、PC之间的数量关系.请直接写出结论，并指出相应的点P与抛物线的位置关系.（说明：点与抛物线的位置关系可以分为三类，例如图②中，点A在抛物线内，点C在抛物线上，点D′在抛物线外.）

参考文献：

[1]王之文.淺谈中考数学试题中的分类讨论及解题应用[J].学苑教育，2013（09）.

[2]周鸣.例谈分类讨论法在中考数学中的运用[J].考试周刊，2014（03）.