基于DIC的预应变下铜/铝复层板各向异性性能检测与研究
孙 涛,梁 晋,郭 翔,李磊刚,任茂栋
(1西安交通大学 机械工程学院,西安710049;2四川工程职业技术学院 机电工程系,四川 德阳618000)
铜以其导电、导热、耐磨、易铸造、力学性能良好的优点,被广泛地应用于电力、电子信息以及传热工程中。但铜资源短缺,而铝资源丰富,因此以铜/铝复层材料代替铜可以大量节约铜资源[1]。很多结构件如散热片、过渡板等,铜/铝复层材料则完全可代替。
近年来,国内外学者对复层板的力学性能进行了研究。Motarjemi等[2]对低碳钢-不锈钢复合板进行了拉伸实验,实验结果与基于传统复合法则预测的结果相符;Yoshida等[3]采用循环施加弯曲载荷的方法,利用数值计算与实验相结合的方法确定了复合板及其组分材料的力学性能参数。刘洪伟等[4]对不同相对厚度比的不锈钢-铝复层材料进行了拉伸实验,基于传统混合法则建立了屈服点、抗拉强度与相对厚度比之间的关系模型。Tseng等[5]对不同厚度比的铜/铝复层板的成形极限进行了研究,并建立了有限元模型对实验进行验证,预测了材料厚度分布、破裂位置和复层板变形行为。复层材料各组分性能差异较大,采用一定方法复合后,在力学上表现出很强的各向异性、非均匀性、非连续性及非线性等性质[6]。各向异性的存在很大程度上会影响板料变形时应力和应变的分布、厚度的减薄和板料的成形性能,通过预应变对板料各向异性进行研究是一种比较有效的方法。Hahm等[7]通过两步预应变,基于混合强化二次屈服函数本构模型对冷轧低碳钢板料在平面应变下的各向异性特性进行了理论探讨,结果表明塑性应变比(r值)分布几乎不受预变形影响。
为了准确获得复层板料的各向异性力学特性,本工作采用三维光学应变测量方法进行应变的测量,克服了传统接触式引伸计、应变片测量方法的不足:测量成本高,抗干扰性低,应力集中部位的测量不准确等[8]。数字图像相关法(Digital Image Correlation,DIC)也叫数字散斑相关法(Digital Speckle Correlation Method,DSCM),是一种典型的光学应变测量方法。这种方法因具有精度高、速度快、易于操作、非接触式、三维全场测量的特点[9],受到国内外学者的广泛关注。
本工作结合数字图像相关法和双目立体视觉技术[10],提出并实现了一种用于爆炸焊接方法制备的铜/铝复层板全场应变测量的方法,基于该方法通过拉伸实验对预应变下的铜/铝复层板各向异性力学性能进行了研究。
1 数字图像相关法理论基础
数字 图 像 相 关 法,由 Petres等[11],Chu等[12]提出,通过跟踪和匹配变形前后所采集图像的灰度信息,来测量物体在各种载荷作用下表面整体的瞬时位移场和应变场。基本原理如图1所示,其中一幅作为参考图像,另外一幅作为待匹配图像,在参考图像中,取以待匹配点 (x,y)为中心的(2M+1)×(2 M+1)大小的矩形子图像,在待匹配图像中,通过一定的搜索方法,并按照某一相关函数进行相关计算,寻找与选定的子图像相关系数最大的以 (x′,y′)为中心的子图像,则点 (x′,y′)即为点 (x,y)在待匹配图像中的对应点[13]。
在进行相关匹配时,左右图像须按照某一映射函数进行计算,本工作采用一阶映射函数,其中包含了旋转、平移、正应变和剪切应变等分量。
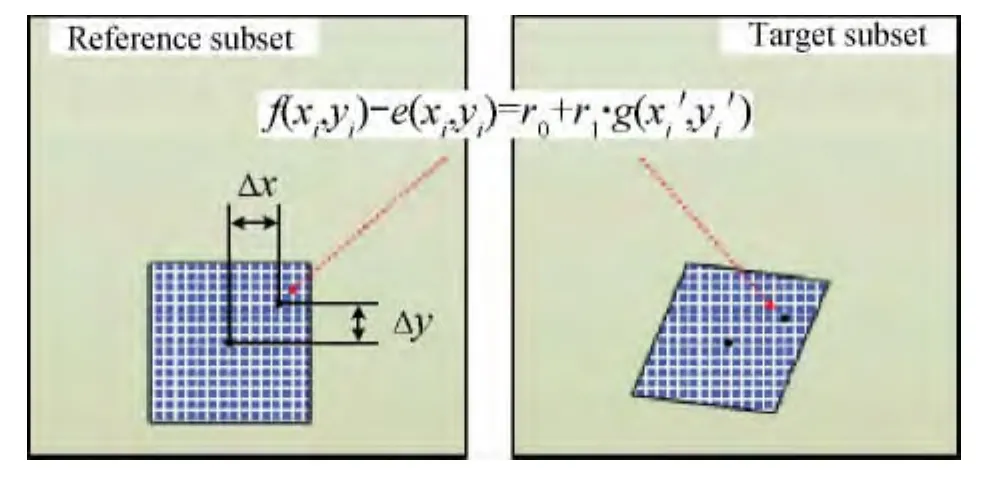
图1 数字图像法原理图Fig.1 Schematic diagram of digital image correlation
点 (xi,yi)的灰度值f(xi,yi)与点(xi′,yi′)的灰度值g(xi′,yi′)之间的关系可表示为:
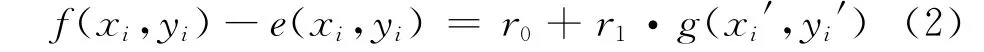
式中:e(xi,yi)表示噪声部分;r0,r1用于补偿由于光照引起的灰度差异。
假设子图像中有n个像素点,像素灰度受到独立同分布的噪声干扰,那么对应的参考子图像和变形子图像间的相似程度通过式(3)衡量:
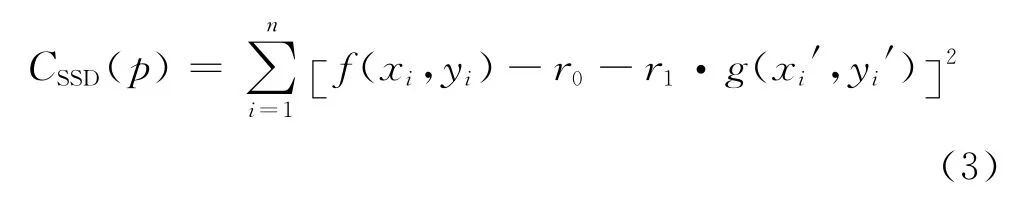
式中:p = [u,ux,uy,v,vx,vy,r0,r1]为 相 关 参 数 向量。式(3)为非线性方程,可利用最小二乘迭代算法求解,但需要给出未知数的初值。通常u,v通过粗匹配获得,其他的未知数如下给出:

然而,误差较大的初值会降低最小二乘迭代算法的计算速度或得到错误的收敛结果。为此,本工作借鉴文献[14]的种子点匹配方法对初值进行计算(如图2所示),具体方法可参考文献[14],本文不再赘述。
匹配完毕后,对于任意一个变形状态的左右两幅子图像中心点,利用三角测量原理即可重建其对应的三维空间坐标。重复上述过程,可以获得若干点的空间坐标,这些空间点经曲面拟合就构成物体表面的三维形貌,进一步计算即可得到被测物表面的三维位移场。最后,在变形前的参考状态中,利用某一点P及其周围4个点建立4个三角形,对于每个三角形,根据其变形前后的边长变化求解得到基于柯西-格林张量的拉格朗日应变,取4个三角形的应变平均值作为点P的应变。

图2 基于种子点的相关匹配 (a)匹配种子点;(b)匹配所有点Fig.2 Correlation matching based seed point(a)seed point is matched;(b)all points are matched
2 实验方法
实验所用材料铜/铝(T2紫铜/1060纯铝)复层板由宝鸡申奥金属材料有限公司提供,经爆炸焊接而成,为消除焊接应力进行了适当热处理[15]。为了增强板料各向异性倾向,分别对12块大试样施加0%,1.5%,2.5%和4.5%的拉伸预应变,拉伸速率为0.5mm/min;然后,分别沿着与预应变后的大试样拉伸方向成0,30,60,90°截取拉伸小试样(截取角度记为φ)进行拉伸实验,拉伸速率为2mm/min,大小试样尺寸如图3所示。所有拉伸试样经线切割和砂纸打磨而成,表面喷涂黑白哑光漆形成黑白相间的随机分布图案,以作为数字图像相关法跟踪被测件表面变形的散斑特征。
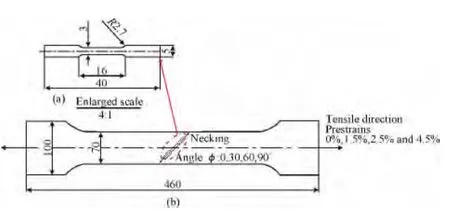
图3 试样预应变示意图 (a)小试样尺寸;(b)大试样尺寸Fig.3 Schematic illustration of prestrain(a)dimensions for small specimen;(b)full size sheets
本工作根据数字散斑相关算法和变形测量理论,基于 Window XP环境,利用VC++6.0研制开发了用于复层板料变形测量的计算软件XJTUDIC/VS,并利用该软件对拉伸实验进行测量和数据分析。实验装置如图4所示,试验机为RGM4100型电子万能材料试验机。实验流程如图5所示,流程中的相机标定可参考文献[16]。
为了验证XJTUDIC/VS系统在材料力学性能实验方面的可行性,采用图4所示的实验装置进行钢试件的标准拉伸实验,并在试件表面布置引伸计用于精度验证和对比。试件材料为Q235钢,厚度2mm,通过线切割加工得到;引伸计标距为50mm,应变测量精度达到0.5%,可测量的最大应变为50%。

图4 基于数字图像相关法的实验装置Fig.4 Experimental setup based on DIC
3 各向异性力学特性的表征
3.1 塑性应变比r

图5 基于数字图像相关法的拉伸实验流程Fig.5 Flow chart of tensile test based on DIC
塑性应变比r(Lankford系数),简称r值,反映了板料沿着平面方向和宽度方向的变形能力,有增量和全量两种形式。r值的全量形式的定义比较简单,但增量形式的定义更加准确[17],所以本工作选用增量形式对板料的各向异性进行表征。


式中:εe表示弹性应变;σ表示应力(本文中出现的下标均代表试样不同的方向:11为长度方向,22为宽度方向,33为厚度方向);ν是泊松比。单向拉伸时,σ22=0,σ33=0,所以式(8)变为:
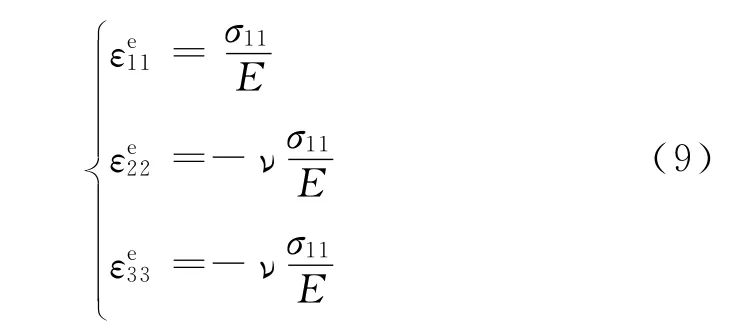
又因材料的变形包括塑性和弹性部分,即

式中:ε代表材料的整体应变;εp为塑性应变。将式(10)带入式(9)可得:
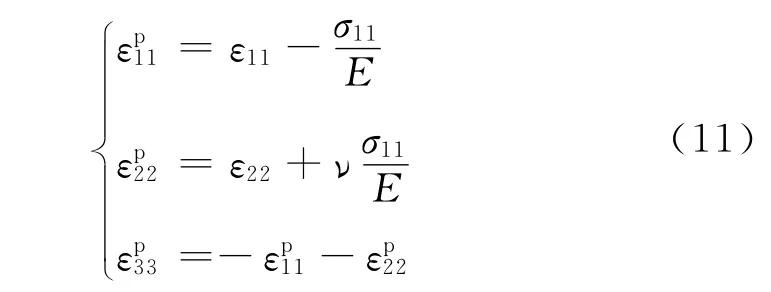
式中的σ11,ε11,ε22,E均由实验得到,带入式(11)可求得,,再带入式(5)即可得到不同方向的r值。
3.2 各向异性指标(IPA)
各向异性指标(Index of Plane Anisotropy,IPA)是针对某一项性能参数来衡量各向异性的指数[18],表达式如式(12)所示。
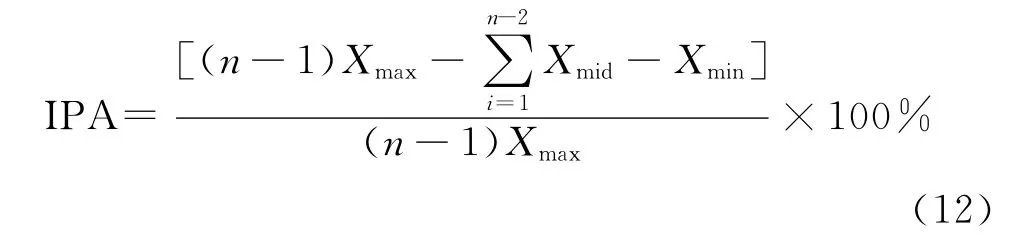
式中:Xmax,Xmin,Xmid分别表示材料某一力学性能的最大、最小及中间各值;n表示材料不同方向的个数。当IPA不大于3.60%时,文献[18]认为各向异性不明显。
4 结果与讨论
4.1 验证实验结果

图6 三维变形场 (a)散斑图;(b)物表应变场Fig.6 Three-dimensional deformation field(a)speckle image;(b)surface strain field
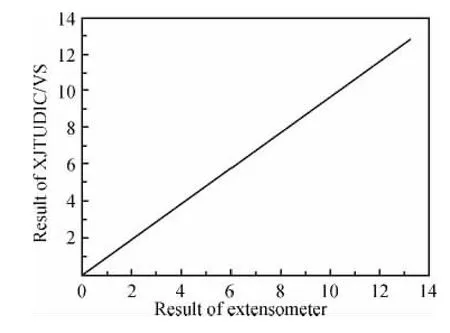
图7 本工作方法与引伸计测量结果对比Fig.7 Comparison of test results with extensometer
图6为验证实验中钢试件被拉伸到缩颈时所采集的图像及软件计算的对应结果。从图6可以看出,试件被拉伸到缩颈时,缩颈区的应变最大。图7为钢制薄板试件拉伸实验中,将不同变形状态下分别利用引伸计和XJTUDIC/VS系统测得的试件表面同一变形区域的平均应变作为x轴和y轴,并对结果进行拟合。拟合直线方程为y=0.9961x+0.005,说明两种方法之间的偏差约为0.4%,因为实验所用引伸计应变测量精度达到0.5%,所以XJTUDIC/VS系统应变测量精度应不低于0.5%。分析误差产生的原因可能包括:(1)引伸计在拉伸过程中相对试件有细微打滑现象;(2)两种方法本身都存在一定的测量误差。实验表明,本工作提出的测量方法能够重建载荷作用下试件表面的变形场,且测量结果能直观显示。
4.2 屈服强度和塑性应变比的变化
在不同的预应变水平下,图8为小试样屈服强度σ0.2与截取角度φ的关系图,图9为小试样塑性应变比r与截取角度φ的关系图。从图8可以看出,随着预应变程度增加,小试样屈服强度σ0.2总体上增大;但随着截取角度φ增大,不同预应变水平下σ0.2的变化趋势不一致,4.5%预应变水平下的变化最为剧烈。由图9可知,当未施加预应变时,r值变化不大;预应变量增加到1.5%时,r值变化明显;预应变量增加到2.5%时,板料平面方向和厚度方向的变化不均匀性有所改善;随着预应变量达到4.5%,r值随φ变化差异又趋明显,说明高预应变量条件下,板料各个方向性能差异很显著。研究表明[19-21],板材在塑性变形过程中会形成织构,使不同方向的力学行为表现出各向异性。铜/铝复层板材在大预应变量条件下r值呈现较强的各向异性可能与塑性变形中形成的织构有关。
4.3 板料力学性能参数的各向异性
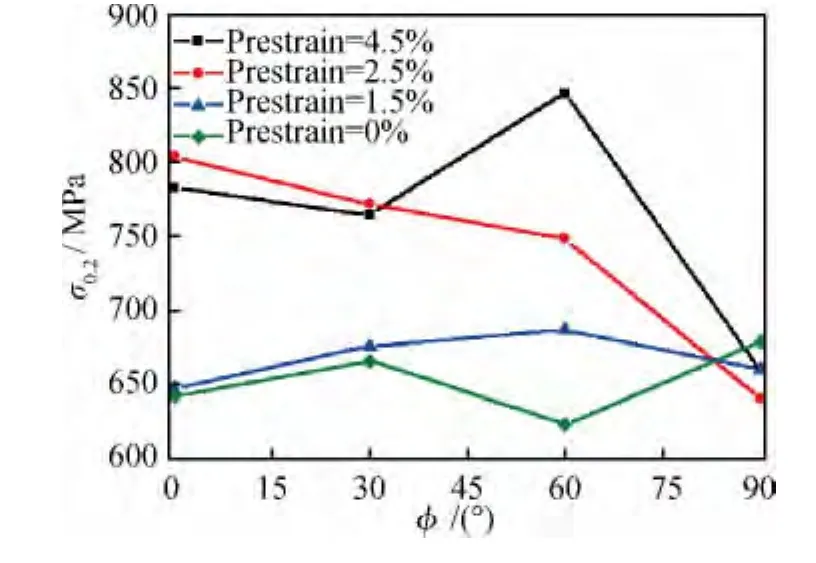
图8 不同预应变下小试样屈服强度与截取角度关系图Fig.8 Uniaxial yield stress for the small specimens applied atφ=0,30,60,90°,respectively
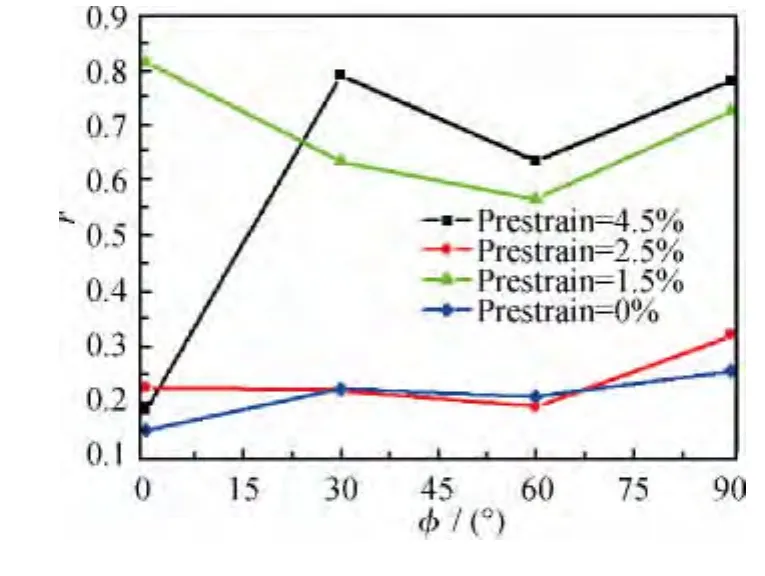
图9 不同预应变下小试样塑性应变比与截取角度关系图Fig.9 Plastic strain ratio for the small specimens applied atφ=0,30,60,90°,respectively
图10是不同预应变水平、不同截取角度的小试样的真实应力-应变曲线,表1所列为复层板料力学性能数据。由图10可知,不论是否施加了拉伸预应变,铜/铝复层板料不同方向的应力-应变曲线分离现象都非常明显,呈现较强的各向异性特征。由表1数据可知,当未施加预应变时,其弹性模量E、抗拉强度σb和断裂伸长率δ的IPA值都小于3.60%,各向异性不明显;当达到2.5%预应变水平时,E,σb和δ的IPA值都达到最大,分别为49.27%,14.71%和15.79%;随着预应变量增加到4.5%时,E,σb和δ的IPA值分别减小到22.75%,8.50%和7.41%,但各向异性依然明显。而对于屈服强度σ0.2来说,其IPA值在预应变为4.5%时达到最大,且各预应变水平下的IPA值都大于3.60%,表现出明显的各向异性,这从图8也能得到验证。总体来看,随着预应变量的增加,铜/铝复层板料力学性能参数的各向异性发展有先增强后减弱的趋势。
4.4 应变硬化率的各向异性
为了进一步探究不同预应变水平下铜/铝复层板料的各向异性,本工作还考察了应变硬化速率与应变之间的关系,如图11所示。当轴向真实应变ε11<0.02时,沿拉伸预应变方向(φ=0°)的应变硬化速率与应变之间的关系受预应变程度影响很小,但其他方向受预应变程度影响就比较显著。随着轴向真实应变的增加,不同预应变水平下的应变硬化速率曲线开始分离,且不同方向的分离程度差异明显,即具有明显的各向异性,但最后应变硬化速率都逐步减小为零。总体上来看,铜/铝复层板料的初始应变硬化率值比较大,然后以指数速率下降到零。
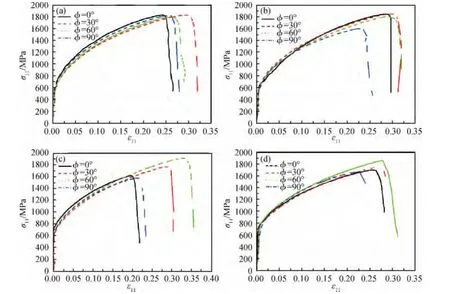
图10 小试样的真实应力-应变曲线 (a)0%预应变;(b)1.5%预应变;(c)2.5%预应变;(d)4.5%预应变Fig.10 True stress-strain curves of the small specimens(a)after 0%prestrain;(b)after 1.5%prestrain;(c)after 2.5%prestrain;(d)after 4.5%prestrain
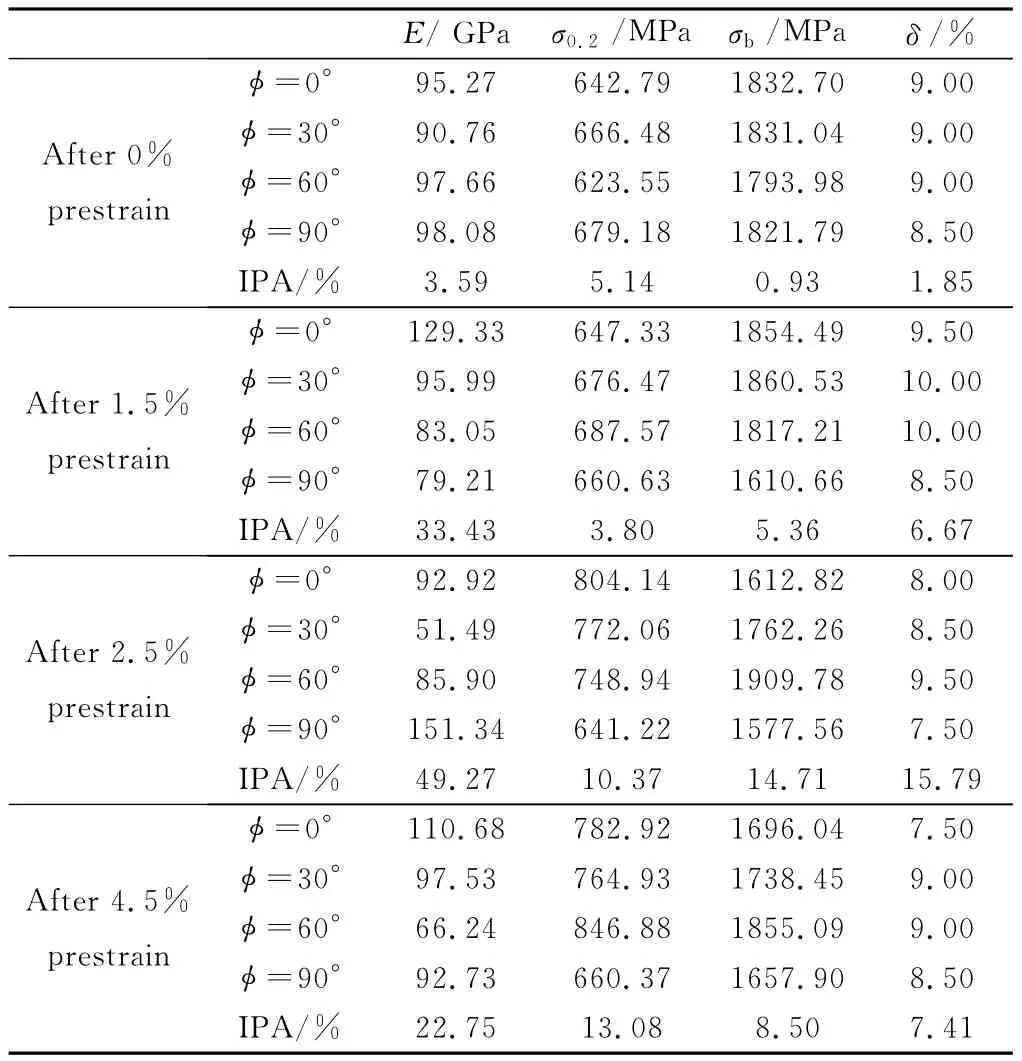
表1 不同方向小试样的力学性能Table 1 Mechanical properties of the small specimens for different loading directions
4.5 各向异性的演化
图12所示为不同预应变水平下相同方向的小试样轴向真实应变ε11与横向真实应变ε22的关系曲线。由图12可以看出,在整个变形过程中,随着变形程度的增加,不同预应变水平下在相同方向的曲线分离程度越来越大,即各向异性程度逐渐增强,这说明铜/铝复层板料的各向异性是随着应变的增加而不断变化的。
5 结论
(1)XJTUDIC/VS系统的应变测量精度高于0.5%,与引伸计基本相当;可以简单、快速、精确地获得铜/铝复层板料在拉伸变形中的三维全场应变数据。
(2)在2.5%预应变水平下铜/铝复层板料的E,σb和δ的IPA值最大,预应变达到4.5%时σ0.2和r的各向异性最明显。总体来看,随着预应变量的增加,铜/铝复层板料力学性能参数的各向异性先增强后减弱,r值的各向异性呈现先增强再减弱又增强的复杂变化。
(3)铜/铝复层板料不同方向的初始应变硬化率值都比较大,随着应变的增加,各方向间差异逐步明显,整体上都以指数速率下降到零。
(4)铜/铝复层板料的各向异性随着应变的增加而不断增强。
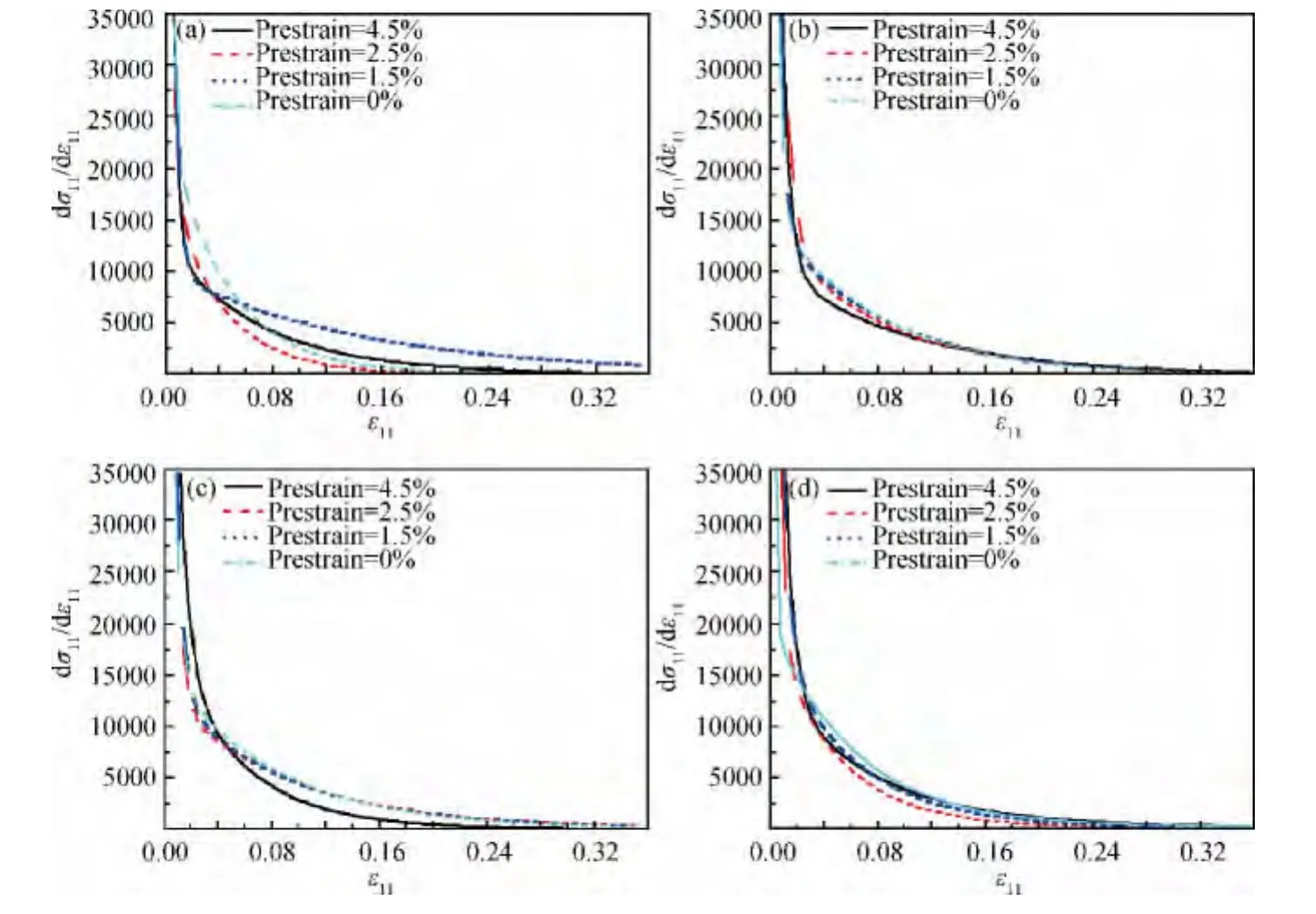
图11 不同预应变下相同方向的小试样应变硬化率曲线 (a)φ=0°;(b)φ=30°;(c)φ=60°;(d)φ=90°Fig.11 Strain-hardening rate of the small specimens for different prestrains(a)φ=0°;(b)φ=30°;(c)φ=60°;(d)φ=90°
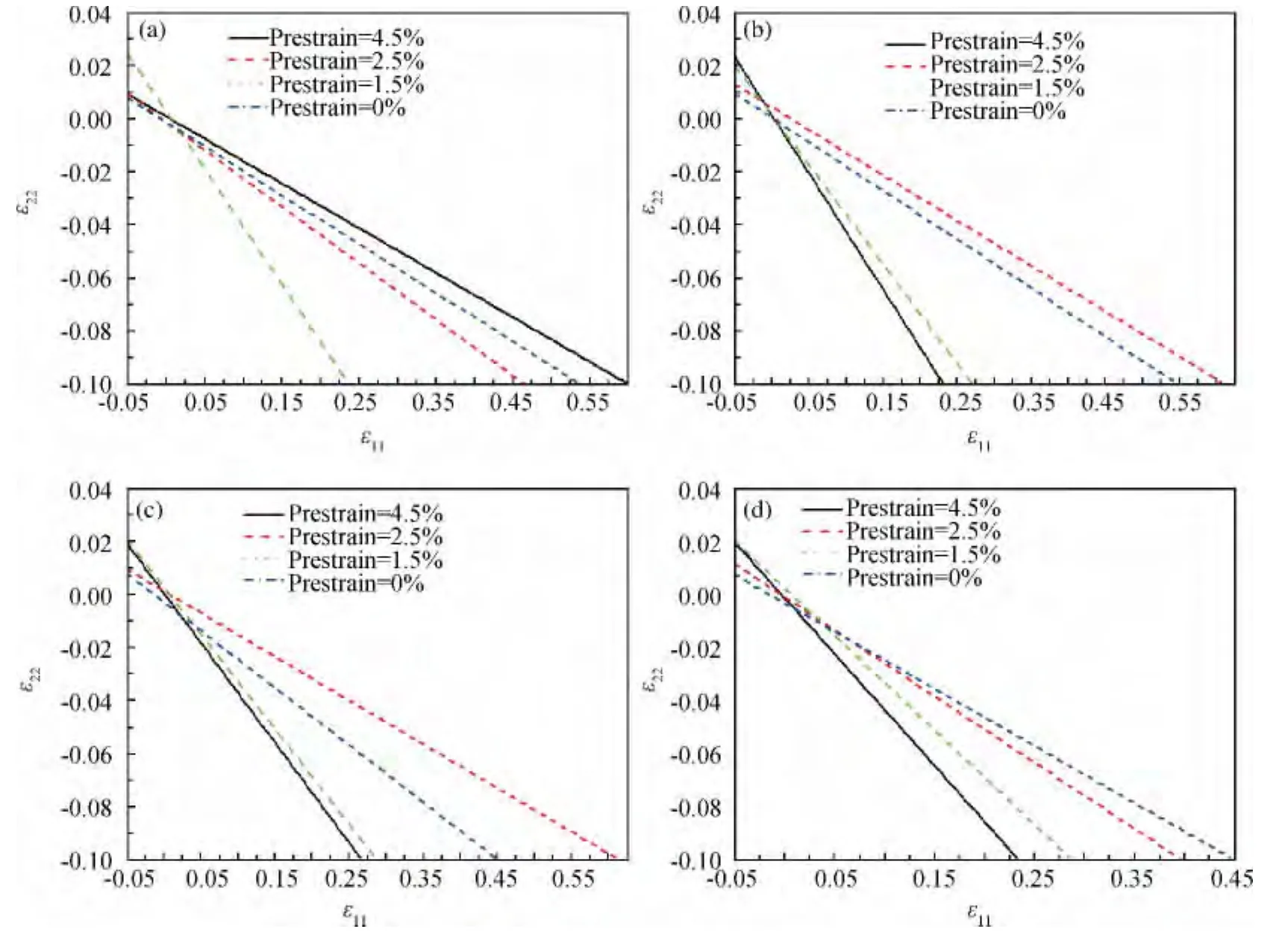
图12 不同预应变下相同方向的小试样轴向应变与横向应变的关系曲线 (a)φ=0°;(b)φ=30°;(c)φ=60°;(d)φ=90°Fig.12 Longitudinal strain vs transverse strain of the small specimens for different prestrains(a)φ=0°;(b)φ=30°;(c)φ=60°;(d)φ=90°
[1] 樊小龙.双金属层合复合材料力学性能的数值模拟[D].重庆:重庆大学,2008.
[2] MOTARJEMI A K,KOCAK M.Mechanical and fracture charaterization of a bi-material sheet plate[J].International Journal of Pressure Vessels and Piping,2002,79(33):181-191.
[3] YOSHIDA F,URABE M,HINO R.Inverse approach to indentification of material parameters of cyclic elasto-plasticity for component layers of a bimetallic sheet[J].International Journal of Plasticity,2003,19(12):2149-2170.
[4] 刘洪伟,郭成,臧顺来.不锈钢-铝合金复层材料拉伸力学性能分析[J].中国机械工程,2007,18(7):862-865.
LIU H W,GUO C,ZANG S L.Analysis of tension property of stainless steel-aluminum alloy clad[J].China Mechanical Engineering,2007,18(7):862-865.
[5] TSENG H C,HUNG C H,HUANG C C.An analysis of the formability of aluminum/copper clad metals with different thicknesses by the finite element method and experiment[J].Int J Adv Manuf Technol,2010,49(9-12):1029-1036.
[6] 田富强.复合材料力学性能的细观有限元分析[D].上海:上海交通大学,2004.
[7] HAHM J H,KIM K H.Anisotropic work hardening of steel sheets under plane stress[J].International Journal of Plasticity,2008,24(7):1097-1127.
[8] HOFFMANN H,VOGL C.Determination of true stress-straincurves and anisotropy in tensile test with optical deformation measurement[J].Annals of the CIRP,2003,52(1):217-220.
[9] CHEN Z X,LIANG J,GUO C,et al.Application of the speckle technique for three-dimensional deformation measurement[J].Optical Engineering,2012,51(1):013604-1-013604-7.
[10] 刘建伟,梁晋,梁新合,等.大尺寸工业视觉测量系统[J].光学精密工程,2010,18(1):126-134.
LIU J W,LIANG J,LIANG X H,et al.Industrial vision measuring system for large dimension work-pieces[J].Optics and Precision Engineering,2010,18(1):126-134.
[11] PETRES W H,RANSON W F.Digital imaging techniques in experimental stress analysis[J].Opt Eng,1982,21(3):427-431.
[12] CHU T C,RANSON W F,SUTTON M A,et al.Applications of digital-image-correlation techniques to experimental mechanics[J].Exp Mech,1985,25(3):232-245.
[13] 唐正宗,梁晋,肖振中,等.用于三维变形测量的数字图像相关系统[J].光学精密工程,2010,18(10):2244-2253.
TANG Z Z,LIANG J,XIAO Z Z,et al.Digital image correlation system for three dimensional deformation measurement[J].Optics and Precision Engineering,2010,18(10):2244-2253.
[14] 唐正宗,梁晋,肖振中,等.大变形测量数字图像的种子点匹配方法[J].西安交通大学学报,2010,44(11):51-55.
TANG Z Z,LIANG J,XIAO Z Z,et al.Digital image correlation method based on seed point for large deformation measurement[J].Journal of Xi’an Jiaotong University,2010,44(11):51-55.
[15] LEE J E,BAE D H,CHUNG W S,et al.Effects of annealing on the mechanical and interface properties of stainless steel/aluminum/copper clad-metal sheets[J].Journal of Materials Processing Technology,2007,187-188:546-549.
[16] 胡浩,梁晋,唐正宗,等.大视场多像机视频测量系统的全局标定[J].光学精密工程,2012,20(2):369-378.
HU H,LIANG J,TANG Z Z,et al.Global calibration for muti-camera videogrammetric system with large-scale field-of-view[J].Optics and Precision Engineering,2012,20(2):369-378.
[17] HANCE B M.Influence of discontinuous yielding on normal anisotropy(R-Value)measurements[J].Journal of Materials Engineering and Performance,2005,14(5):616-622.
[18] JATA K V,HOPKINS A K,RIOJA R J.The anisotropy and texture of Al-Li alloys[J].Materials Science Forum,1996,217-222:647-652.
[19] 陈振华,夏伟军,程永奇,等.镁合金织构与各向异性[J].中国有色金属学报,2005,15(1):1-11.
CHEN Z H,XIA W J,CHENG Y Q,et al.Texture and anisotropy in magnesium alloys[J].The Chinese Journal of Nonferrous Metals,2005,15(1):1-11.
[20] BOHLEN J,NÜRNBERG M R,SENN J W,et al.The texture and anisotropy of magnesium-zinc-rare earth alloy sheets[J].Acta Materialia,2007,55(6):2101-2112.
[21] KALIDINDI S R.Modeling anisotropic strain hardening and deformation textures in low stacking fault energy fcc metals[J].International Journal of Plasticity,2001,17(6):837-860.

