超材料在宽频微波衰减吸收材料中的应用研究进展

周卓辉，黄大庆，刘晓来，牟维琦，康飞宇

（1北京化工大学 理学院，北京100029；2北京航空材料研究院，北京100095；3清华大学 材料学院，北京100083）

超材料是一种由金属和介质复合而成的具有负折射率性质的人工电磁材料［1，2］。最初研究超材料时，人们主要关注的是如何实现其等效负折射率、等效负介电常数［3，4］和等效负磁导率［5］，设计出一系列的结构去实现超材料的左手性质，例如开口谐振环（Split Ring Resonator，SRR）［2］、S 形 谐 振 环［6］，螺 旋 线 结构［7］等。通过构建渐变的电磁参数去实现隐身斗篷也是人们的关注点之一［8］，然而超材料的最大特点是通过超材料结构的设计实现人们所需要的折射率、介电常数和磁导率，这就为超材料在吸波材料上的应用提供了有利条件。众所周知，实现隐身材料优良吸波性能的两个关键因素之一是实现材料与空气的阻抗匹配［9］，因此，理论上可以通过对超材料结构的设计获得实现阻抗匹配所需要的电磁参数，从而实现入射波的零反射。2008年，Landy等［10］首先提出了由电谐振器、电介质基板和金属微带线构成的具有“完美吸收”特点的电磁耦合结构吸波体，之后人们对超材料吸波体的完美吸收产生了极大的兴趣，提出了各种结构的超材料吸波体去实现各种波段的电磁波吸收［11，12］，同时设计了一系列结构去改善电磁波极化对超材料吸波体的影响［13，14］。但是，对于吸波材料来说，其最重要的应用条件是能否在宽频带上实现高吸收，所以制约超材料吸波体发展的一个重要因素就是如何把窄频段的完美吸收变成宽频带的完美吸收。

本文主要对不同超材料吸波体的频带扩展方法的研究现状进行了综述，其中包括基于谐振吸收、加载集总元件、加载电阻材料的频带扩展方法以及通过可调超材料去实现超材料吸波体的智能化吸收和宽频吸收的方法，最后，重点分析了分形学曲线在超材料设计中的应用。

1 基于金属谐振吸收的宽波段超材料吸波体

通过近年来对超材料的研究发现，超材料作为吸波材料最基本的吸波方式是通过入射电磁波的激励，在平行金属结构上产生电谐振，环状金属结构内产生磁谐振，使入射电磁波能量在谐振结构中来回震荡从而消耗吸收［10］。平行板结构相当于电容（C），环状结构相当于电感（L），其谐振频率是由等效电容和电感构成的LC电路决定的［11］。改变超材料的结构参数相当于改变了LC电路中的电容和电感值，进而移动谐振频点。所以改变超材料的结构参数容易造成其谐振中心频率位置的改变，于是人们想通过对不同谐振单元的复合以及组合来实现超材料吸波体的频率扩展。

Tao等［15］提出了一种SRR的复合结构，将两个不同大小的SRR模型连接起来构成超材料。由于不同的结构具有不同的谐振频率，所以通过实验得到了两个吸收波段，其吸收率在1.4THz和2.9THz分别达到了86%和84%；进一步对表面电流进行分析，发现大尺寸的SRR主要吸收低频的入射电磁波，而小尺寸的SRR主要吸收高频的入射电磁波，从而实现双峰吸收。

Li等［16］对SRR单元结构的排列方式进行了调整，在这个结构中，每一个单一的单元都包含了四个小的SRR基本单元，通过中心电容的开口方向与入射电磁波电场方向的对应方式不同而实现不同波段的吸收；经过实验分别在11.15GHz和16.01GHz左右实现了99.9%的吸收率，峰的半波宽度也分别达到了0.32GHz和0.62GHz，表面电流的分析显示，开口与电场垂直SRR对低频电磁波的吸收起主导作用，开口与电场平行的SRR对高频电磁波的吸收起主导作用，从而实现了双吸收峰。

Luo等［17］和Sun等［18］分别在双吸收峰的基础上进行了进一步扩展；Luo提出了一种由五个不同尺寸的SRR排列而成的超材料结构（图1），由于尺寸不同，每个SRR都有一个吸收峰，所以从材料的整体性能来看，其吸波性能就是这五个SRR吸收峰的叠加，每个SRR的吸收峰半波宽度约为0.4GHz，整个材料的吸收峰半波宽度就被扩展到了1.3GHz［17］。

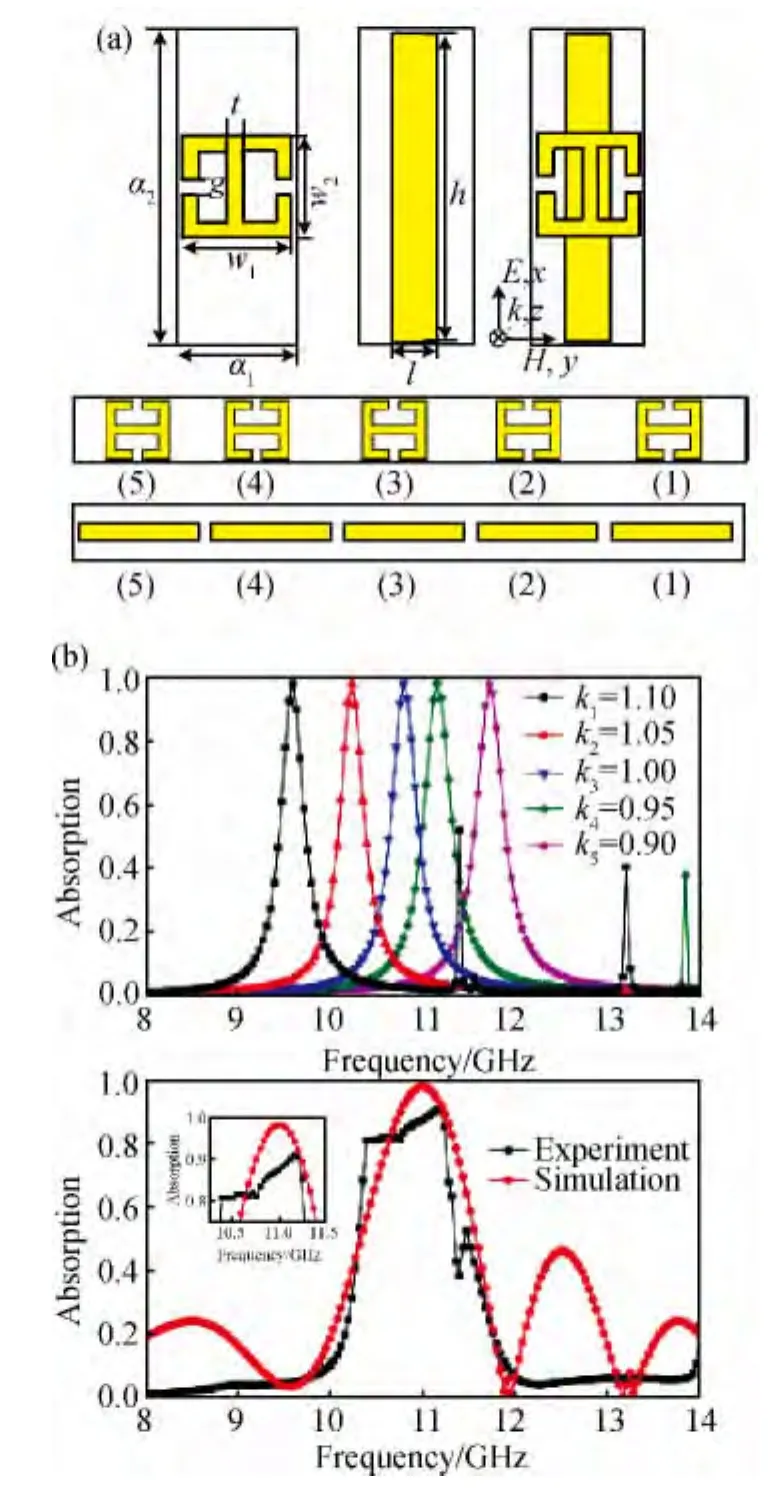
图1 SRR的平行排列［17］ （a）原理图；（b）吸收曲线Fig.1 Parallel arrangement of SRR［17］（a）schematic；（b）absorbing curve

Sun提出在高度上层层叠加的结构设计方案［18］，他提出的材料在吸波机理上与Luo提出的结构不同，该方案是通过结构参数设计使每层结构的折射率不同从而使入射波和反射波干涉相消达到吸波的目的。模拟上，吸波体在5～30GHz的范围内能达到－10d B以上的吸收，实验上，在10～30GHz的范围内实现了－10d B以上的吸收。

上述这种频带扩展的方法是基于电磁谐振吸收，存在谐振吸收频带窄的缺点，多个或者多层谐振单元的组合虽然可以扩展吸收带宽，但是其频带扩展能力有限，并且是以牺牲整体的厚度为代价，因此人们需要在其他的影响因素中寻找突破点。

2 基于电阻损耗吸收的宽波段超材料吸波体

由于金属结构消耗入射电磁波能量的能力有限，所以其谐振吸收峰都比较窄，如何改变谐振吸收中电磁波的消耗机制，或增加其消耗从而加深单独吸收峰的吸收带宽成为人们研究的重点。

与传统的主要由电磁谐振吸波的频带扩宽方法不同，顾超等［19］提出一种加载集总元件的宽频超材料吸波体（图2），所设计的超材料吸波体的结构单元由加载集总元件的磁谐振器、介质基板和金属背板组成，认为相对于不加载集总元件的磁谐振器，加载集总电容能够增强电路的储能能力或空间中电磁能转换成电路中电能的能力，加载集总电阻能够增强电路消耗电能的能力，两者合在一起能够增强磁谐振器对空间中电磁波的吸收。他仿真了加载集总元件和不加载集总元件两种情况下的电磁波吸收率，结果显示在加载集总元件的情况下能够极大地增加电磁波的吸收带宽，说明在加载的情况下，集总元件主要起到了消耗入射电磁波的作用，从而实现了宽频吸收。但是，该方案加工成本较高，工艺上难以大规模制作，于是孙良奎等［20］设计了一种基于电阻材料的超材料吸波体，由周期性排列的电阻片、基体以及金属背底构成；与传统金属超材料吸波体的谐振吸收机理不同，这种吸波体是由入射电磁波在周期性的电阻片上产生感应电流，电流转变成热能损耗而进行吸波。他们通过仿真计算和优化得到了一种反射率在8～18GHz范围内小于－10dB的吸波材料，并且采用手糊工艺制备了空心石英纤维增强环氧树脂基体，丝网印刷制备了电阻片，实现了所设计的吸波材料，其实验结果与设计结果比较吻合。根据此能量消耗方式屈绍波等［21］也设计了一种由六边形电阻膜、介质基板和金属背板构成的超材料吸波体，仿真得到的反射率和吸收率表明，该吸波体在7.0～27.5GHz之间对入射电磁波具有宽频带的强吸收，证实了电路谐振相对于电磁谐振更易于实现宽带吸波的特点，并且由于六边形结构的旋转对称性，此结构还同时实现了极化不敏感的特性。在前人的研究基础上，程用志等［22］同时设计了三种类型的吸波体，比较了其吸波性能，并分析了其优劣。这三种吸波体分别为基于正方形金属贴片（Square Metal Patch，SMP）结构的超材料吸波体、电阻型频率选择表面（Resistance Frequency Selective Surface，RFSS）吸收体以及SMP结构与RFSS结构复合的吸波体。模拟结果表明，在2～30GHz频率范围内，SMP吸波体通过几何参数的设计可以实现多频窄带强吸收，这时电磁谐振起主要的吸收作用，RFSS吸收体则通过方块电阻实现高频宽带强吸收，但其带宽扩展有限。而结合SMP和RFSS两者优点的复合结构吸波体，在3～25GHz之间的吸收率都大于90%以上。

图2 加载集总元件［19］ （a）原理图；（b）吸收曲线对比Fig.2 Loaded lumped components［19］ （a）schematic；（b）comparison of the absorbing curve

加载集总元件可以拓宽电磁波吸收带宽，但是以牺牲整体材料厚度为前提，并且其制作工艺复杂，不利于实际大规模应用；而基于电阻片的超材料吸波体其厚度难以达到要求，并且不能大范围地扩宽吸收带宽，这也在一定程度上限制了其应用，在这两者之间寻找一个最佳的结合点是超材料吸波体未来发展的一个研究重点。

3 可调宽波段超材料吸波体

改变结构参数可以很容易调节谐振吸收频点，但在应用中超材料的结构参数本身并不容易改变，因此，如何通过任意改变超材料的结构参数去实现超材料吸波体的智能化吸收和宽频吸收特性是人们一直以来重点关注的问题。

Gil等［23］报道了一种基于SRR可调超材料实现方案，提出将可变二极管负载在谐振环上实现可调性能，于是在长方形开口谐振环的内长方形和外长方形之间加载可变二极管，通过调节二极管上的电压来调节谐振环的谐振频率。Aydin等［24］报道了负载电容器的同心圆形状的SRRs超材料，他们将电容器分别加载在SRRs外环的开口处、内环的开口处和内环与外环的间隙处［24］，通过实验和模拟双重手段给出在这三种条件下，调节不同的电容值可以获得不同的谐振频率，结果显示，当电容器加载在外环开口处时能够实现最大谐振频率的改变。

Ekmekci等［25］提出一种基于SRR微小缝隙结构的设计方案，每一个微小的缝隙都有两个状态，通过微电子机械系统（Micro Electronic Mechanical Systems，MEMS）的开关技术可以改变微小缝隙的“开”“关”状态，从而调节其吸收频带的位置，并且可以简单计算出，当有3个微小带隙的时候，不同“开”“关”状态的组合就能实现7个频段的吸收。他们给出了不同数量缝隙结构的不同吸收频段，同时还将不同的结构排列在一起实现了多个带宽的吸收，但是他们还没有在实验中设计出开关去实现微小缝隙的开关状态，未达到可调的目的。

Ye等［26］也提出了相似的SRR微小缝隙结构的设计方案，讨论了通过不同数量和不同结构的排列方式实现多带宽的吸收，但他们也未提出如何设计MEMS去调节SRR上微小缝隙结构的开关状态。

Hand等［27］从理论和实验上分析了如何通过在谐振环开口上加载MEMS系统去实现对磁谐振的调节，分别总结了MEMS系统在谐振环上并联和串联结构的优缺点，并在串联的情况下实现了不同频带电磁波吸收的调节，其设计思路和Gil等［23］的很相近，然而，MEMS系统的尺寸太大，不可能应用在微小的带隙上去实现其可调性能。

上述可以看出，加载集总元件和通过MEMS系统控制开关状态实现可调宽频超材料吸波体在实际应用中还存在很大的困难，并且增加了超材料的整体尺寸，对于大规模的应用更是一种挑战，因此，这种可调宽频超材料还有待进一步的研究。

4 基于分形学的宽频超材料设计

2002年Engheta［28］提出一种由超材料表面构成的超薄吸收屏，与传统超材料结构设计方案不同的是，构成这种超材料表面的结构是希尔伯特曲线，他从理论上计算出这种超材料表面可以表现出高的阻抗，形成高阻抗表面，实现与空气的阻抗匹配进而实现电磁波的高吸收。随后 Mcvay等［29，30］进一步研究了不同阶数的希尔伯特曲线和皮亚洛曲线构成的超材料表面的谐振规律，他们发现阶数越高其谐振频率越低，并且指出，由希尔伯特曲线等该类分形学曲线所构成的超材料的最大优势是可以用非常小的周期单元实现低频的谐振。

2009年Noor等［31］研究了双层希尔伯特曲线构成的超材料吸波体的吸波性能，重点观察了介质层参数对此超材料吸波体吸波性能的影响，同年，作者就该结构对电磁波极化的响应作了更深入的研究［32］，实验测量了其单站雷达散射面积，结果表明，入射波极化方式对该结构的吸波性能影响不大，分析其面电流分布情况之后发现，出现这种特点的原因是因为其不同结构对入射波极化响应不同，从而整体上表现出极化不敏感的特点。

根据分形学思想，张燕萍等［33］设计了一种基于树枝结构的超材料吸波体（图3），虽然结构不是严格的分形学图案，但是每一级树枝结构确实带有分形的特点。仿真结果表明，每一级树枝结构都产生了一个吸收峰，进一步通过对树枝结构尺寸的调节使三个吸收峰扩展成为一个完整的吸收峰从而实现了9.7～11.7GHz的宽吸收。由于此树枝结构的旋转对称性，所以这种超材料吸收体同时具有各向同性、宽吸收带宽、高吸收率等优点。

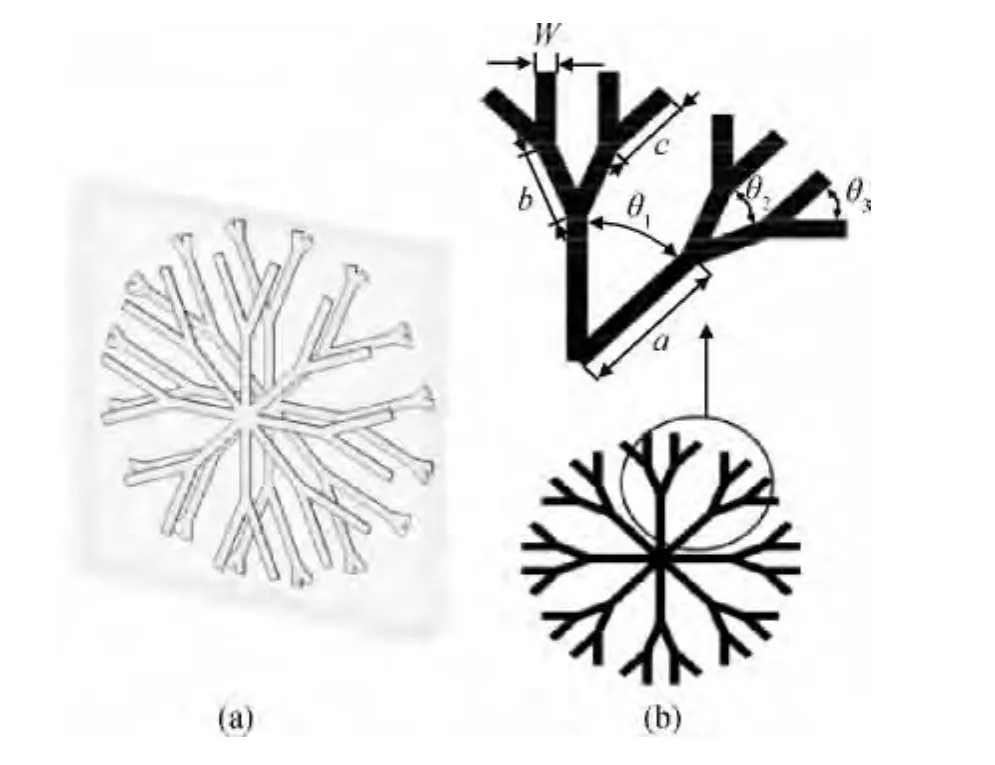
图3 设计样品示意图［33］ （a）基本结构单元；（b）树枝单元结构Fig.3 The illustration of the design［33］（a）basic unit of the structure；（b）branching structure

根据传统SRR结构吸波机理的研究和分析可以看出，SRR结构吸波就是LC谐振吸波［11］，分析其谐振规律可知，当SRR结构的线宽越大，环的圈数越多，其谐振频率越低，因此想获得低频吸收，SRR结构需要较大的尺寸，这就导致在非谐振频段，SRR超材料结构会有很大的反射，这不利于扩展超材料吸波体的带宽；而引入分形学曲线可改善这个问题，因为分形学曲线的最大优点就是能在很小的尺寸下实现低频的谐振［29，34］。与此同时，分形学图案的每一级都相当一个微小的谐振单元，不需要牺牲吸波体的厚度去实现多频段谐振，所以分形学图案可能是未来超材料吸波体设计发展的一个理想方案。

综上所述，不同结构超材料吸波体的吸波机理及其优缺点如表1所示，由机理对比分析可以看出，超材料获得吸波性能最根本的方法是通过金属单元的谐振吸收。而加宽其吸波频带的方法一是通过多单元结构的设计实现多带宽吸收［16，17］，二是通过加大消耗从而增加单峰的吸波带宽［20］。仅仅从方法本身来看，多单元结构容易实现多带宽吸收，却不容易实现宽频吸收，改变消耗机制能增加单峰的带宽却不容易大规模制作。因此如何将这两个方法有效地结合起来是未来超材料吸波体发展成为宽频吸波材料的必经途径。

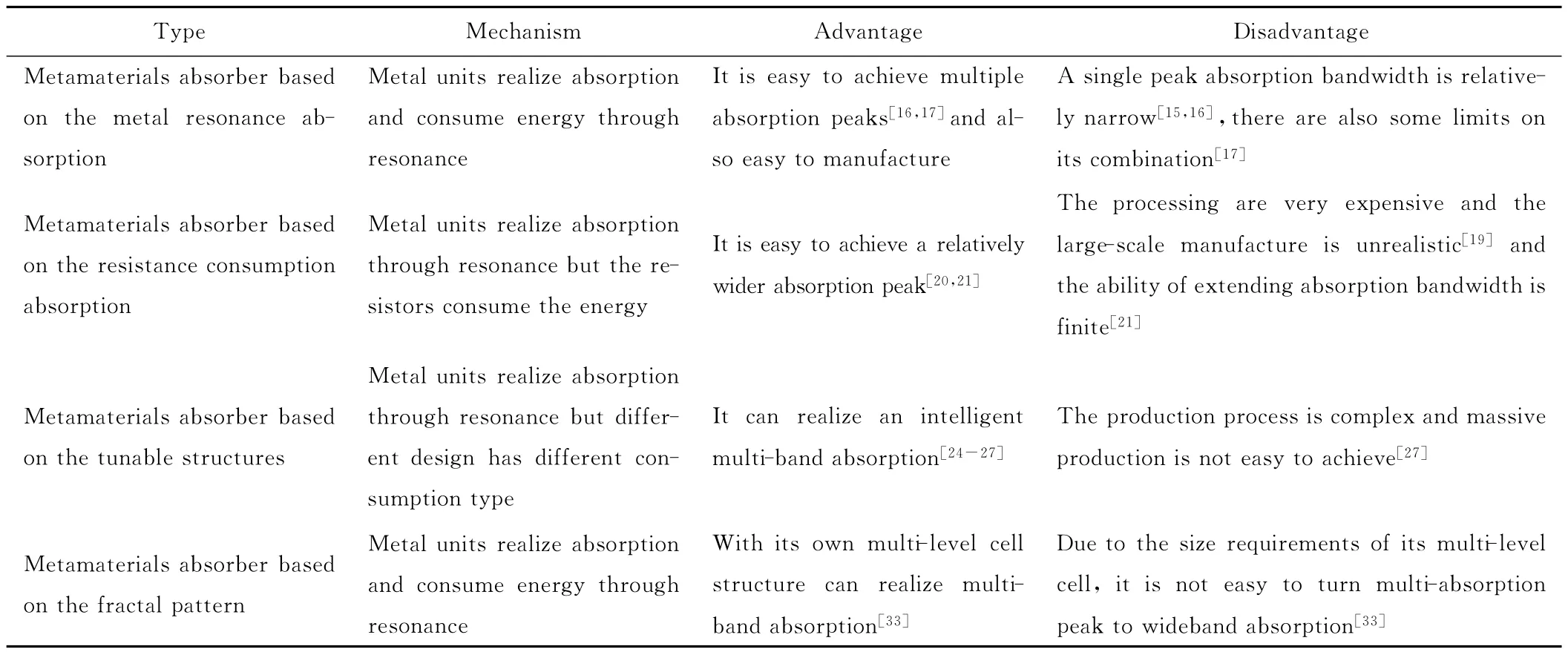
表1 不同吸波体的优缺点比较Table 1 The comparison of the advantages and disadvantages of different absorber

5 结束语

本文主要对超材料吸波体频带扩展的规律及其不同扩展途径的研究现状进行了综述，总结了不同超材料吸波体的吸波机理及其优缺点，重点分析了基于分形学曲线的超材料设计方案及其作为吸波体的设计方案的特点，其很小的尺寸可以实现低频谐振以及分形学图案本身所具有的多级多谐振频率的特征都可以用于吸波带宽的扩展，这就为超材料吸波体宽频衰减吸收性能的发展提供了重要的研究方向。

［1］ VESELAGO V G.The electrodynamics of substances with simultaneously negative values ofεandμ［J］.Sov Phys Usp，1968，10（4）：509－514.

［2］ SMITH D R，PADILLA W J，VIER D C，et al.Composite medium with simultaneously negative permeability and permittivity［J］.Phys Rev Lett，2000，84（18）：4184－4187.

［3］ PENDRY J B，PENDRY A J，STEWART W J.Extremely low frequency plasmons in metallic mesostructures［J］.Physical Re－view Letters，1996，76（25）：4758－4776.

［4］ PENDRY J B，HOLDEN A J，ROBBINS D J.Low frequency plasmons in thin－wire structures［J］.J Phys Condens Matter，1998，10（22）：4785－4809.

［5］ BROWN J.Artificial dielectrics［J］.Progress in Dielectrics，1960，2：195－225.

［6］ KHAN M F，MUGHAL M J.Modified single side paired S－ring resonators［A］.3rd International Congress on Advanced Electromagnetic Materials in Microwaves and Optics［C］.London：IEEE，2009.522－524.

［7］ BAENA J D，MARQUES R，MEDINA F，et al.Artificial magnetic metamaterial design by using spiral resonators［J］.Physical Review B，2004，69（1）：014402.

［8］ LIU R，JI C，MOCK J J，et al.Broadband ground－plane cloak［J］.Science，2009，323（5912）：366－369.

［9］ 刘凌云，胡长寿，郭彪.超材料吸波体吸波特性研究［J］.材料导报，2010，24（5）：1－3.

LIU Ling－yun，HU Chang－shou，GUO Biao.Research on absorbing properties of metamaterial absorber［J］.Materials Review，2010，24（5）：1－3.

［10］ LANDY N I，SAJUYIGBE S，MOCK J J，et al.Perfect metamaterial absorber［J］.Physical Review Letters，2008，100（20）：207402.

［11］ WAKATSUCHI H，PAUL J，GREEDY S，et al.Cut－wire metamaterial design based on simplified equivalent circuit models［J］.IEEE Transactions on Antennas and Propagation，2012，60（8）：3670－3678.

［12］ LIU X L，STARR T，STARR A F，et al.Infrared spatial and frequency selective metamaterial with near－unity absorbance［J］.Physical Review Letters，2010，104：207403.

［13］ 胡长寿，刘凌云，裴嘉政.对电磁波极化不敏感超材料吸波体的研究［J］.光学与光电技术，2010，8（4）：83－86.

HU Chang－shou，LIU Ling－yun，PEI Jia－zheng.Study on a polarization insensitive metamaterial absorber［J］.Optics ＆ Optoelectronic Technology，2010，8（4）：83－86.

［14］ CHENG Y，YANG H，CHENG Z，et al.Perfect metamaterial absorber based on a split－ring－cross resonator［J］.Applied Physics A，2010，102（1）：99－103.

［15］ TAO H，BINGHAM C M，PILON D，et al.A dual band terahertz metamaterial absorber［J］.Journal of Physics D：Applied Physics，2010，43（22）：225102.

［16］ LI M H，YANG H L，HOU X W，et al.Perfect metamaterial absorb with dual bands［J］.Progress in Electromagnetics Research，2010，108：37－49.

［17］ LUO H，WANG T，GONG R Z，et al.Extending the bandwidth of electric ring resonator metamaterial absorber［J］.Chin Phys Lett，2011，28（3）：034204.

［18］ SUN J B，LIU L Y，DONG G Y，et al.An extremely broad band metamaterial absorber based on destructive interference［J］.Optics Express，2011，19（22）：21155－21162.

［19］ 顾超，屈绍波，裴志斌，等.基于磁谐振器加载的宽频带超材料吸波体的设计［J］.物理学报，2011，60（8）：662－667.

GU Chao，QU Shao－bo，PEI Zhi－bin，et al.Design of a wide－band metamaterial absorber based on loaded magnetic resonators［J］.Acta Physica Sinica，2011，60（8）：662－667.

［20］ 孙良奎，程海峰，周永江，等.一种基于超材料的吸波材料的设计与制备［J］.物理学报，2011，60（10）：750－754.

SUN Liang－kui，CHENG Hai－feng，ZHOU Yong－jiang，et al.Design and preparation of a radar absorbing material based on metamaterial［J］.Acta Physica Sinica，2011，60（10）：750－754.

［21］ 顾超，屈绍波，裴志斌，等.基于电阻膜的宽频带超材料吸波体的设计［J］.物理学报，2011，60（8）：668－672.

GU Chao，QU Shao－bo，PEI Zhi－bin，et al.Design of a wide－band metamaterial absorber based on resistance films［J］.Acta Physica Sinica，2011，60（8）：668－672.

［22］ 程用志，聂彦，龚荣洲，等.基于超材料与电阻型频率选择表面的薄型宽频带吸波体的设计［J］.物理学报，2012，61（13）：130－136.

CHENG Yong－zhi，NIE Yan，GONG Rong－zhou，et al.Design of a thin wide－band absorber based on metamaterials and resistance frequency selective surface［J］.Acta Physica Sinica，2012，61（13）：130－136.

［23］ GIL I，BONACHE J，GARCIA－GARCIA J，et al.Tunable metamaterial transmission lines based on varactor－loaded split－ring re－sonators［J］.IEEE Transactions on Microwave Theory and Techniques，2006，54（6）：2665－2674.

［24］ AYDIN K，OZBAY E.Capacitor－loaded split ring resonators as tunable metamaterial components［J］.Appl Phys，2007，101（2）：024911－1－024911－5.

［25］ EKMEKCI E，TOPALLI K，AKIN T，et al.A tunable multiband metamaterial design using micro－split SRR structures［J］.Optics Express，2009，17（18）：16046－16058.

［26］ YE Q W ，LIN H，CHEN X Q，et al.A tunable metamaterial absorber made by micro－gaps structures［A］.2011 Cross Strait Quad－Regional Radio Science and Wireless Technology Conference［C］.Harbin，China：IEEE，2011.234－237.

［27］ HAND T，CUMMER S.Characterization of tunable metamaterial elements using MEMS switches［J］.IEEE Antennas and Wireless Propagation Letters，2007，6：401－404.

［28］ ENGHETA N.Thin absorbing screens using metamaterial surfaces［A］.Antennas and Propagation Society International Symposium［C］.San Antonio，Texas：IEEE，2002.392－395.

［29］ Mc VAY J，ENGHETA N，HOORFAR A.High impedance metamaterial surfaces using Hilbert－Curve inclusions［J］.IEEE Microwave and Wireless Components Letters，2004，14（3）：130－132.

［30］ Mc VAY J，HOORFAR A，ENGHETA N.Thin absorbers using space－filling－curve high－impedance surfaces［A］.Antennas and Propagation Society International Symposium［C］.Washington DC：IEEE，2005.22－25.

［31］ NOOR A，HU Z.Effects of spacer parameters on resistive Hilbert curve array absorbers［A］.Microwave Conference，2009.APMC 2009.Asia Pacific［C］.Singapore：IEEE，2009.602－605.

［32］ NOOR A，HU Z.Dual polarised wideband metamaterial radar absorbing screen based on resistive Hilbert curve array［J］.Electronics Letters，2009，45（2）：130－131.

［33］ 张燕萍，赵晓鹏，保石，等.基于阻抗匹配条件的树枝状超材料吸收器［J］.物理学报，2010，59（9）：6078－6083.

ZHANG Yan－ping，ZHAO Xiao－peng，BAO Shi，et al.Dendritic metamaterial absorber based on the impedance matching［J］.Acta Physica Sinica，2010，59（9）：6078－6083.

［34］ YOUSEFI L，RAMAHI O M.Artificial magnetic materials using fractal Hilbert curves［J］.IEEE Transactions on Antennas and Propagation，2010，58（8）：2614－2622.