双向玻纤织物复合材料双轴拉伸载荷下的力学行为

蔡登安，周光明，王新峰，钱 元，刘伟先

（南京航空航天大学 机械结构力学与控制国家重点实验室，南京210016）

纤维增强复合材料以其轻质、高强以及抗疲劳、耐高温、可设计等一系列优点，在航空、航天制造领域获得了广泛应用［1，2］。双向玻纤织物复合材料是指在互相垂直的两个方向上同时具有增强玻璃纤维交错排列的一种复合材料［3］。该种材料在纵、横向都具有良好的力学性能，克服了单向纤维复合材料横向性能弱的缺点，因而得到了较多的应用。同时，随着纤维增强复合材料在航空、航天结构中应用水平的不断提高，复合材料在复杂应力状态下的力学行为逐渐成为人们关注的热点，尤其是双轴或多轴加载状态下的力学性能研究。

近年来，关于玻璃纤维增强复合材料双轴加载问题国外已经开展了不少实验和理论研究，主要集中在单向玻璃纤维增强复合材料及其层合板的研究上，对双向玻纤织物复合材料提及甚少，如Mailly在单向纤维增强复合材料单轴拉伸实验的基础上，使用不同形状和尺寸的横向加载臂，设计出单向复合材料双向拉伸的十字型试件［4］；Smits等［5］和 Makris等［6］以玻璃纤维增强复合材料层合板为基础，深入研究了双轴加载十字型试件的设计、优化与实验；Lamkanfi等［7，8］和Antoniou等［9］基于三维有限元分析模型，对单向纤维增强复合材料层合板进行了数值模拟，对双轴加载应变分布及破坏区域进行了预测；Moreno等［10］根据双轴加载仿真与实验，拟合了纤维增强复合材料在拉－拉象限的强度包络线。在国内，由于实验条件的限制及缺乏统一的规范，对这方面的研究还比较少，对双轴加载问题的研究也主要侧重于金属和理论分析层面，王颖晖提出了功能材料双轴加载的十字板试件设计的优化方案［11］；吴向东等［12］建立了臂上开缝十字形试件双向拉伸实验有限元计算模型，分析了板料的变形行为；任家陶等［13］研究分析了钛板双向拉伸的强化效应。对于纤维增强复合材料的双轴加载问题，陆晓华自行设计了双轴加载实验设备，对两种纤维增强复合材料1∶1双轴拉伸行为进行了探索［14］，但由于实验条件的限制而未能深入研究。

本工作在现行双轴加载实验方法的特点和适用性的基础上，设计了双向玻纤织物复合材料十字型试样，进行了该材料的单轴与双轴拉伸实验，研究了双向玻纤织物复合材料在复杂载荷条件下的力学行为。

1 实验

1.1 试样制备

双向玻纤织物由南京玻璃纤维研究设计院提供，环氧树脂为WSR618，环氧固化剂为苯二甲胺，增塑剂为邻苯二甲酸二丁酯。根据双向玻纤织物复合材料的特点，设计四个加载臂之间以锥形圆角过渡形式的十字型试样，采用模压成型工艺制备。试样铺层方向相同，层数为18，试样尺寸及实貌如图1所示。

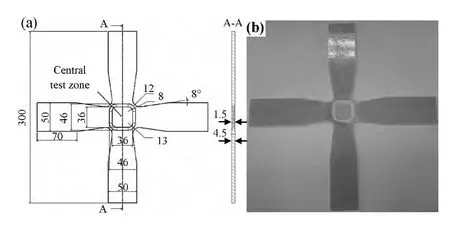
图1 十字型试样 （a）几何尺寸；（b）试样实貌Fig.1 Cruciform specimen （a）geometry；（b）morphology

1.2 单轴拉伸实验

实验在WDW－E200D电子万能试验机上进行，使用DH－3818－2静态应变测试仪采集应变数据。单轴拉伸试样尺寸为250mm×25mm×2mm；采用位移控制加载，加载速率为1mm／min。

1.3 双轴拉伸实验

双轴拉伸实验在SDS100双轴四缸电液伺服动静试验机上进行。该试验机采用最新研制的数字式电箱，其内部采用模块化设计，全部操作和设置均由系统软件的虚拟面板实现。它具有位移、负荷、变形三种控制方式，四缸均独立控制，每缸最大加载±100k N，最大加载位移±60mm，可实现任意比例的双轴加载实验。

设计的双向玻纤织物复合材料双轴拉伸十字型试样满足如下条件：（1）中心实验区应力分布均匀；（2）中心实验区剪应力最小；（3）中心实验区外的应力集中最小；（4）中心实验区应力水平较高，以保证初始破坏发生在实验区。

本工作研究的双向玻纤织物复合材料为正交各向异性材料，在纵向（X轴）和横向（Y轴）具有相同的力学性能。同时设计了载荷比f（Y轴与X 轴的载荷之比）分别为1／1，1／2，1／4的双轴拉伸实验，实验过程如图2所示。为了测量试件中心实验区的应力水平，且考虑到试件正反两面可能受力不够均匀，因此在中心实验区中心正反两面各贴了两组0°，90°应变片。实验加载采用负荷控制，加载速率为f×0.01k N／s，确保载荷按比例匀速、准确施加到十字型试样上。

图2 双向玻纤织物复合材料双轴拉伸实验Fig.2 Biaxial tensile testing of the bidirectional glass fiber fabric composites

2 结果与讨论

2.1 双轴拉伸模量特性

定义双向玻纤织物复合材料在双轴载荷作用下中心实验区的真实应力为：

式中：Fi为十字型试样i方向加载臂上的外载荷；Ai为试样i方向加载臂端部横截面面积；ηi为中心实验区承力系数。

中心实验区承力系数是指在一定外载荷下，中心实验区平均应力（本工作取实验区中心点纵向和横向应力）与名义应力（纵向和横向加载臂所受外载荷／加载臂截面积）的比值，采用有限元数值仿真方法确定。此承力系数在加载过程中保持不变，并据此计算实际实验时中心实验区的应力水平及破坏应力。本工作采用的十字型试样具有几何对称性，获得的中心实验区承力系数在纵横向是相同的，但不同的载荷比对应的中心实验区承力系数不同。对应载荷比为1／1，1／2，1／4的中心实验区承力系数分别为0.63，0.71，0.75。

双向玻纤织物复合材料拉伸模量测试结果如表1所示。本工作定义双轴拉伸平均模量为应力－应变曲线的割线模量，单轴拉伸平均模量为应力－应变曲线线性段直线模量；定义各载荷比下两方向上平均拉伸模量较大值为该载荷比下材料的双轴拉伸模量，与单轴拉伸模量的比较结果列于表1中。

表1 双向玻纤织物复合材料单轴和双轴拉伸模量Table 1 Uniaxial and biaxial tensile modulus of the bidirectional glass fiber fabric composite

从表1中可以看出，与单轴拉伸模量相比，双向玻纤织物复合材料的双轴拉伸模量明显增加。等比例双轴拉伸载荷下，双轴拉伸模量比单轴拉伸模量增加10.1%；载荷比为1／2的双轴拉伸载荷下，双轴拉伸模量增加16.5%；载荷比为1／4时双轴拉伸模量增加38.2%，增幅最大。由此可见，双轴拉伸载荷对双向玻纤织物复合材料的拉伸模量具有一定的强化作用，且双轴拉伸模量随载荷比的减小而增大。

双向玻纤织物复合材料单轴拉伸应力－应变曲线如图3所示。可以看出，加载初始时期，材料的单轴拉伸应力－应变保持着线性关系；随着载荷的增大，应力－应变关系逐渐从线性过渡到非线性阶段，说明材料内部已经出现一定的破坏，材料的弹性模量有所降低；加载末期，曲线迅速下降，试样突然破坏，表明双向玻纤织物复合材料单轴拉伸呈现非线性与脆性破坏。

图3 复合材料单轴拉伸应力－应变曲线Fig.3 Stress－strain curve of the composite under uniaxial tensile

图4 复合材料双轴拉伸应力－应变曲线（a）f＝1／1；（b）f＝1／2；（c）f＝1／4Fig.4 Stress－strain curves of the composite under biaxial tensile （a）f＝1／1；（b）f＝1／2；（c）f＝1／4

图4为双向玻纤织物复合材料双轴拉伸应力－应变曲线。对比图3可知，材料在双轴拉伸载荷下表现出更为明显的非线性关系，与材料在单轴拉伸后期拉伸模量随载荷的增加而减小不同，材料的双轴拉伸模量随载荷的增加而增大。对比表1可知，等比例双轴拉伸时，材料两个方向的拉伸模量均有所增加，但增幅不大，表现出明显的非线性关系，如图4（a）所示；非等比例双轴拉伸载荷对材料双轴拉伸模量的强化作用表现不平衡，载荷比为1／2和1／4时，X轴向载荷分别为Y轴向载荷的2倍和4倍，X轴向较大的拉伸载荷引起材料Y轴向拉伸模量的显著增加，且X轴向载荷越大，材料Y轴向拉伸模量增幅越大，如图4（b），（c）所示；而材料X轴向本身的平均拉伸模量并未因其拉伸载荷的增大而增大，相反还有一定的减小趋势，说明双轴拉伸载荷对材料的双轴拉伸模量的强化作用与较大载荷加载方向有关。由图4曲线可以看出，无论是材料的X轴向还是Y轴向在应力－应变曲线末端的上升趋势均比较急剧，切线斜率不断增加，说明随着双轴拉伸载荷的增大，材料两个方向的拉伸模量均呈现一定的强化作用。

2.2 双轴拉伸强度与破坏形式

为了研究双向玻纤织物复合材料的双轴加载强度，表2给出了双向玻纤织物复合材料双轴拉伸强度与单轴拉伸实验结果的对比。双轴承载强度由双轴载荷中最大极限载荷计算得到。从表2中可以看出，与双轴拉伸模量的强化作用相反，双向玻纤织物复合材料的双轴拉伸强度存在明显的双向弱化效应，并且随着载荷比增大，材料的双向弱化效应越明显。等比例双轴拉伸时，材料的双轴拉伸强度仅为单轴的60.5%，材料的双向弱化效应最为显著。分析认为，材料强度存在双向弱化的原因是：双向玻纤织物复合材料本身存在一定量的微裂纹，根据断裂力学的相关理论分析，裂纹在双轴拉伸应力状态下更容易扩展，从而导致材料的双轴拉伸强度较低；同时，由于材料的制备工艺导致其界面性能的下降，也会造成复合材料双轴拉伸强度降低。因此，在双向玻纤织物复合材料的结构研究与分析中应充分重视其强度双向弱化效应的影响。

表2 双向玻纤织物复合材料单轴和双轴拉伸强度Table 2 Uniaxial and biaxial tensile strength of the bidirectional glass fiber fabric composite

图5所示为双向玻纤织物复合材料单轴拉伸破坏形式。可以看出，靠近试样端部位置和部分试样中部位置断裂；有明显的断口，断面上纤维断裂；试样侧面凸起，出现明显分层。影响双向玻纤织物复合材料破坏的因素有多种，不仅与纤维和基体的力学性能有关，还与纤维束的形状、分布以及体积分数密切相关；同时，增强相与基体间的界面状况、工作环境以及加载形式对材料的破坏也具有非常重要的影响。在单轴拉伸载荷作用下，双向玻纤织物试样受拉应力，纤维、基体和界面同时承载。随着载荷的增加，叠层玻纤布间较薄弱的界面及基体先行失效，出现分层；纤维继续承载，继而纤维断裂。加载端部的应力集中效应使得界面和基体失效提前，引起靠近试样加载端部附近位置的纤维断裂，界面间的剪切作用也加速了试样的破坏。

图5 复合材料单轴拉伸破坏形式Fig.5 Failure forms of the composite under uniaxial tensile

图6所示为双向玻纤织物复合材料不同载荷比下的双轴拉伸破坏形式。双轴加载方向为双向玻纤织物复合材料的两个纤维增强方向。一般情况下，复合材料层合板在平行于层合方向拉伸载荷作用下的失效模式主要有基体失效、分层和纤维断裂。在不同的双轴载荷下，材料的破坏形式有所不同。

试样等比例双轴拉伸的破坏形式主要表现为试样中心实验区纤维断裂，破坏发生在实验区域，如图6（a）所示。断口方向约沿中心实验区对角线方向，这与实验区最大主应力方向与X轴成45°夹角的理论分析结果相一致。从断口面来看，该破坏特征与单轴拉伸破坏形式不同，等比例双轴拉伸破坏未出现明显的纤维布分层的现象，纤维和基体的失效属拉伸脆性破坏。

如图6（b）所示，载荷比为1／2时的破坏裂纹方向与X轴约成30°角。随着载荷增大，试样中心实验区部分区域基体逐渐破坏失效，同时属于应力集中部位的加载臂根部倒角位置与中心实验区同步产生裂纹，并由此向实验区内部延伸。破坏形式与等比例双轴拉伸类似，主要以纤维断裂为主，同时也伴有一定的实验区纤维布分层现象。

图6 复合材料双轴拉伸破坏形式 （a）f＝1／1；（b）f＝1／2；（c）f＝1／4Fig.6 Failure forms of the composite under biaxial tensile （a）f＝1／1；（b）f＝1／2；（c）f＝1／4

载荷比为1／4时的破坏形式如图6（c）所示。宏观裂纹方向近似呈关于Y轴对称的双抛物线，中心实验区基体大面积失效，层间脱粘，出现较明显分层，层间剪切作用不容忽略。失效模式与单轴拉伸破坏特征较为相似，但与载荷比为1／1和1／2的双轴拉伸破坏形式差别较大，界面分层及纤维断裂方向主要沿载荷较大的加载方向。

3 结论

（1）双向玻纤织物复合材料在单轴拉伸载荷下加载初期表现为线性、脆性断裂行为，但在加载后期出现一定的非线性，材料的拉伸模量随载荷的增大而降低；双轴拉伸载荷下材料表现为显著的非线性行为，材料的双轴拉伸模量随载荷的增大而增大，双轴拉伸载荷对材料的拉伸模量具有一定的强化作用。

（2）与双轴拉伸模量的强化作用相反，双向玻纤织物复合材料在双轴拉伸载荷下的强度特性表现为明显的双向弱化效应，等比例双轴拉伸载荷下材料双轴拉伸强度的双向弱化最显著，仅为单轴拉伸强度的60.5%。

（3）载荷比为1／1和1／2的双轴拉伸载荷下材料的失效模式主要表现为纤维断裂；载荷比为1／4的双轴拉伸载荷下材料的失效特征与单轴载荷下的失效模式相似，主要表现为基体失效和玻纤布分层。

［1］ 杜善义.先进复合材料与航空航天［J］.复合材料学报，2007，24（1）：1－12.

DU S Y.Advanced composite materials and aerospace engineering［J］.Acta Materiae Compositae Sinica，2007，24（1）：1－12.

［2］ 刘代军，陈亚莉.先进树脂基复合材料在航空工业中的应用［J］.材料工程，2008，（增刊1）：194－198.

LIU D J，CHEN Y L.Application of advanced polymer matrix composites in aviation industry［J］.Journal of Materials Engineering，2008，（Suppl 1）：194－198.

［3］ 沈观林，胡更开.复合材料力学［M］.北京：清华大学出版社，2006.

［4］ MAILY L，WANG S S.Recent development of planar cruciform experiment on biaxial tensile deformation and failure of unidirectional glass／epoxy composite［J］.Journal of Composite Materials，2008，42（13）：1359－1379.

［5］ SMITS A，Van HEMELRIJCK D，PHILIPPIDIS T P，et al.Design of a cruciform specimen for biaxial testing of fibre reinforced composite laminates［J］.Composites Science and Technology，2006，66（7－8）：964－975.

［6］ MAKRIS A，VANDENBERGH T，RAMAULT C，et al.Shape optimisation of a biaxially loaded cruciform specimen［J］.Polymer Testing，2010，29（2）：216－223.

［7］ LAMKANFI E，Van PAEPEGEM W，DEGRIECK J，et al.Strain distribution in cruciform specimens subjected to biaxial loading conditions.Part 1：two－dimensional versus three－dimensional finite element model［J］.Polymer Testing，2010，29（1）：7－13.

［8］ LAMKANFI E，Van PAEPEGEM W，DEGRIECK J，et al.Strain distribution in cruciform specimens subjected to biaxial loading conditions.Part 2：influence of geometrical discontinuities［J］.Polymer Testing，2010，29（1）：132－138.

［9］ ANTONIOU A E，Van HEMELRIJCK D，PHILIPPIDIS T P.Failure prediction for a glass／epoxy cruciform specimen under static biaxial loading［J］.Composites Science and Technology，2010，70（8）：1232－1241.

［10］ MORENO S M C，LÓPEZ CELA J J.Failure envelope under biaxial tensile loading for chopped glass－reinforced polyester composites［J］.Composites Science and Technology，2011，72（1）：91－96.

［11］ 王颖晖，方岱宁.功能材料双轴拉伸十字板试件的优化设计［J］.力学学报，2002，34（5）：705－714.

WANG Y H，FANG D N.Optimal design of biaxial tensile cruciform specimens for smart materials［J］.Acta Mechanica Sinica，2002，34（5）：705－714.

［12］ 吴向东，万敏，周贤宾.十字形双向拉伸试验有限元模拟分析［J］.塑性工程学报，2001，8（2）：57－59.

WU X D，WAN M，ZHOU X B.FEM simulation and analysis of cruciform biaxial tensile test［J］.Journal of Plasticity Engineering，2001，8（2）：57－59.

［13］ 任家陶，李冈陵，豆志武，等.双向拉伸实验的进展与钛板双向拉伸的强化研究［J］.实验力学，2001，16（2）：196－206.

REN J T，LI G L，DOU Z W，et al.Biaxial tension test and the strengthening of titanium sheets under biaxial tension［J］.Journal of Experimental Mechanics，2001，16（2）：196－206.

［14］ 陆晓华.双轴纤维增强复合材料强度准则研究与双向拉伸试验［D］.南京：南京航空航天大学，2007.