天线阵元相位中心的一种测量方法

任晓飞，赵 地，龚书喜，金元松

（1.中国电波传播研究所，青岛 266107；2.西安电子科技大学天线与

微波技术重点实验室，西安 710071；3.中国电子科技集团公司第54研究所，石家庄 050081）

0 引 言

当前复杂环境下无线电定位和宽带数字波束合成是电子通信领域的重要研究热点［1］，而高精度的测向技术、波束合成技术大都需要天线的相位中心作为参考建立阵列流型［2-3］。随着通信系统的发展，天线系统也越来越复杂，而如何寻找复杂天线的相位中心就显得尤为重要。文献［4］～［5］曾给出对数周期天线的可变相位中心计算方法，理论上可以计算互耦情况下阵列天线的相位中心，但是随着阵列数目的增加，计算复杂度会显著地提高。文献［6］通过反复迭代的方法计算出了单个对数周期偶极子天线的相位中心。文献［7］以阵列分析理论为基础，求解了场相位方向图和相位中心的关系，计算了阵列天线的相位中心。文献［8］对单个天线的相位方向图进行了实测，不断调整参考点，通过最小二乘法精确估算天线相位中心，并研制出了实际的测试系统，得到了较高精度的相位中心位置，然而对于数个波长的大尺寸天线阵列，移动天线阵元进行测试就不太可能。当多个天线阵元同时存在时，如何准确地测量阵元相位中心位置目前还未看到相关研究。

大多数天线没有固定的相位中心，但是很多天线能够在主瓣范围内找到一个近似稳定的相位中心，通常这样的相位中心被称为“视在相位中心”。即使是“视在相位中心”，可能有的天线在空间辐射方向上不同的截面（E面或H面）也不相同［9］。在具体工程应用中，人们往往更关注主波束范围内视在相位中心，本文主要解决主波束范围内视在相位中心的测量问题。

通过对天线阵列接收到的信号相位差与其相位中心关系的分析，导出了目标函数，利用最小二乘逼近方法求得实际阵列天线“视在相位中心”。这种新的方法能够测得的存在互耦情况下天线阵元的相位中心，无需高复杂度计算，对工程中阵元相位关系处理具有指导意义。最后通过实际天线阵列的数据验证了该方法的有效性。本文中时间因子选取ejωt。

1 阵元相位差与其相位中心的数学关系

为了准确表示阵元相位差与其相位中心的关系，需要保证组成阵列的各个阵元具有较高的幅相一致性，这一点在实际中也常常能够得到保证。建立如图1坐标系，设有P个相同的阵元组成均匀圆形阵列，对于某一来波方向，其中N个子阵元处在主波束范围内，由于阵列均匀、中心对称性，耦合相同，那么这N个子阵元的相位中心分布在同一圆周。设阵元相位中矢径为r′，来波信号矢径为r。

图1 阵元分布坐标系

对于阵元本身的远场电场某一极化分量在其本地坐标系下可以写成：

式中：f（θ，φ）为阵元幅度方向图；φ（θ′，φ′）为参考点取阵元本身相位中心的相位方向图。

当把相位因子归算于统一坐标系下原点，考虑远区场时，θ′＝θ，φ′＝φ，相位项中rp＝r-＾r·r′，距离项中rp≈r。故在统一坐标下远场区电场可改写为：

式中：k＝k，k＝2π／λ，为波数。

那么对于某一信号，其来波方向为（θ，φ），照射到天线阵列，子阵中各个阵元收到的信号相位为：

式中：（θ，φn）为第n个子阵元相位中心相对于来波方向的夹角。

根据相位中心的含义，其在各个方向上构成等相的原则，并考虑到各个阵元的幅相一致性，则有：

那么，对于式（3）中各个方程进行两两相减，得到：

设阵元以夹角为β均匀分布在平面圆周上，在主波束观测区域内各个子阵元的相位中心可以认为近似分布在同一圆周上，则式（5）在直角坐标下展开写成：

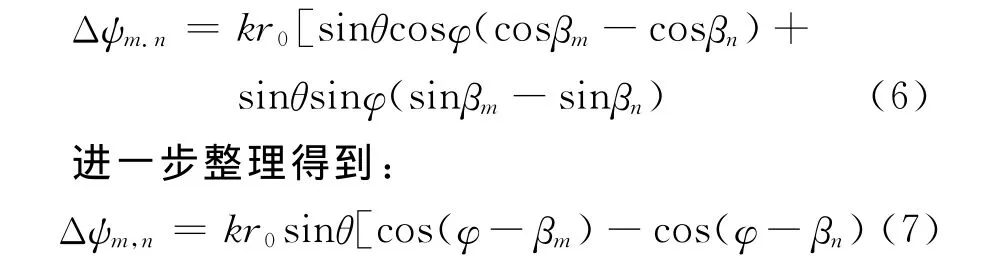
式中：r0为阵元相位中心到圆心距离；βm、βn分别为第m、n个阵元与x轴夹角；Δψm，n为相位差。

在实际信号鉴相过程中，相位差数据都包含噪声在内的各种误差，通过式（7）求解相位中心时会造成一定的误差，此时可利用最小二乘逼近方法求解相位中心位置。令：

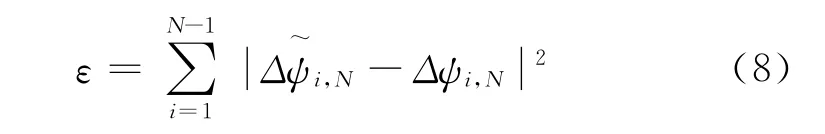
通过求出使ε最小的r0，即得到相位中心。

2 实验结果及分析

实验测试框图如图2所示，利用发信机在天线阵列近似远场区发射共极化信号，多通道接收机同时对天线阵元接收到的信号进行放大、滤波、检波、鉴相，得到信号实测相位。

图2 实验测试系统框图

实验模型中，发信源由扫频信号源、宽带辅助发射天线、GPS接收机构成。GPS用于确定信号源位置。测量接收部分由天线阵列、天线放大器、模拟信道、多信道数字接收机及终端显示组成，信号鉴相过程由快速傅里叶变换提取完成。接收天线阵列为对数周期天线圆形阵列，工作频率80～1 350MHz，天线波束方向指向圆心，阵列口径4.4m。图3给出了利用本文方法实测的相位中心与理论相位中心的对比结果。

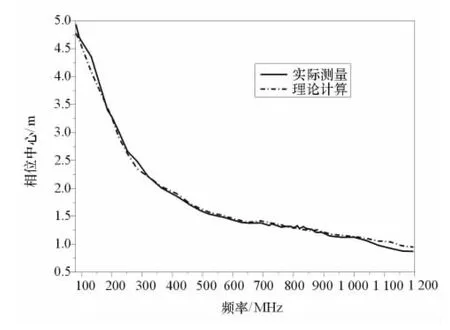
图3 实际测量与理论计算相位中心对比

从图3结果得出，利用式（8）反演得到相位中心与理论计算的相位中心位置在大部分频段都非常吻合，符合对数周期天线视在相位中心随频率变化的规律。在高频端实测的相位中心位置比理论值偏小，更靠近馈电点，这是由于实际天线存在一定缩波，而在理论计算时并未考虑这一点；同时在频率低端相位中心位置超出阵列口径，因为在频率低端相邻阵元间距电长度非常小，耦合很强，导致相位中心位置在阵列外侧。

图4给出了在1 200MHz下，来波方向-3°时，各个天线阵元基线间相位差关系图。从图中可以明显看到，实测阵元相位差比理论计算要小，偏离来波方向越大阵元表现越明显。

图4 相位差随阵元分布图

如果利用式（8）得到相位中心来表征阵元之间的相位关系，可以有效改善高频端实测相位与理论相位差偏差大的现象，如图5所示。

图5 修正后相位差随阵元分布图

为进一步验正测量相位中心的有效性，利用来波方向-3°情况下实际测量反演的相位中心，计算7.1°来波方向下各阵元基线相位差，并与在该方向设置辐射源测试结果对比。图6给出了1 062MHz基线相位差对比情况。

从图6中明显看到，依据反演测量得到相位中心计算得到的相位差与实际测量相位非常吻合，有效地修正了纯理论计算的误差。进一步的实际测试验证了在其他更多的角度上，反演测量的相位中心依然具有有效性。

图6 7.1°方向各阵元相位差对比图

在实际实测过程中，可以增加方位面上空间采样点，在许多不同方向上进行测试，反演得到各自测试方向上的视在相位中心，把这些各自的相位中心进行平均处理，可以有效减小每次测量过程中引入的误差，必要的是这些测试方向需要保持在天线主瓣范围内。

3 结束语

虽然大部分天线阵元存在“相散”特性，但是在天线主波束范围内，一般都能够找到近似的视在相位中心，而且该相位中心一般能够满足大部分的系统需要，诸如干涉仪测向、宽带波束合成、数字阵列分析等。通过对对数周期天线阵列进行外场实际测试，得到天线阵元的实测相位关系，利用最小二乘法反演出阵元的相位中心位置。通过实际测试数据与理论数据的分析、对比，验证了该方法的有效性。由于实际的对数周期天线在高频端存在一定的缩波，实测的相位中心更靠近馈电点，测量的相位中心能够有效表征阵元之间的相位关系。本文研究的方法是基于互耦均匀的阵列展开，实际中还有一部分阵列是非均匀阵列，此时由于互耦各不相同，各个阵元相位中心相互独立，此种情况下相位中心位置的测量还有待进一步研究。

［1］ 潘宝凤.通信侦察系统总体设计技术［J］.电讯技术，2011，51（6）：1-5.

［2］ 洪伟.一种对修正MUSIC算法的改进测向方法［J］.舰船电子对抗，2011，34（3）：71-73.

［3］ 赵地，任晓飞.相关干涉仪测向原始样本的求解方法［J］.舰船电子对抗，2012，35（6）：55-58.

［4］ 金元松，任晓飞，冀海鸣，等.对数周期偶极子天线全空间可变相位中心［J］.电波科学学报，2007，22（2）：229-233.

［5］ 金元松，董眀玉，何绍林，等.对数周期偶极子天线的可变相 位 中 心 ［J］.电 波 科 学 学 报，2001，16（3）：323-328.

［6］ 丁晓磊，王建，林昌禄.对数周期偶极子天线相位中心的 分 析 与 计 算 ［J］.电 子 学 报，2003，31（9）：1375-1377.

［7］ 陈曦，傅光，龚书喜，等.阵列天线相位中心的计算与分析［J］.电波科学学报，2010，25（2）：330-335.

［8］ 尚军平，傅德民，邓颖波.天线相位中心的精确测量方法研究［J］.西安电子科技大学学报，2008，35（4）：673-677.

［9］ Prata A Jr.Misaligned Antenna Phase-Center Determinaton Using Measured Phase Patterns.IPN Progress Report［R］.California：Jet Propulsion Laboratory，California Institute of Technology，2002.