多平台对单目标的被动跟踪系统研究

刘晓锋

（中国电子科技集团公司第20研究所，西安 710068）

0 引 言

对目标跟踪一般分为主动式和被动式两种，主动跟踪利用传感平台向目标区域发射电磁信号并接收目标反射的回波信号，从而获取目标的参数信息。被动跟踪是通过接收目标辐射源信号对目标进行跟踪。主动跟踪具有全天候、高精度等优点，它广泛应用在国防、交通等领域。但平台在主动跟踪中容易被敌方侦察，研究具备隐身能力的探测系统成为需求。而被动目标跟踪技术具有隐蔽性强、能反电子侦察、抗电子干扰等优点［1］，其合乎现代作战的要求，因此被动目标跟踪技术成为国内外学者研究的热点。文献［2］提出基于量测确定的定位线的空间几何关系和卡尔曼滤波法对目标进行被动跟踪，但过分依赖目标与平台的几何关系，若平台机动性强，则这种几何关系变得更加复杂，容易导致定位跟踪失败。文献［3］给出机载单平台对机动目标定位与跟踪方法，但其依靠平台的运动，定位跟踪实时性不强。而多平台对目标定位跟踪具有实时性、高精度和可靠性，从而能满足现代一体化战争的需求。

1 单目标被动跟踪系统结构

多平台对单目标被动跟踪系统可分为伪线性模型系统和非线性模型系统。前者首先将观测方程转换成伪线性，其次利用线性相关技术从而估算出目标的运动信息。文中建立基于纯方位信息的伪线性量测方程，利用最小二乘法得到目标位置的粗估计值，然后将其作为卡尔曼滤波的输入进行结果平滑处理，具体系统结构如图1所示。

图1 伪线性模型跟踪系统结构

非线性模型系统结构可分为集中式和分布式两种。集中式处理结构，可以利用传感器的原始量测数据，没有任何信息的损失，因而融合跟踪的结果是最优的［4］。为了便于对伪线性模型系统和非线性模型系统进行对比研究，文中提及的非线性模型系统指集中式结构，它将纯方位量测送给处理中心，然后采用并行滤波（量测扩维）技术解算出目标运动状态。并行滤波可以选用非线性滤波技术，例如扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）等，文中非线性滤波指EKF。非线性模型跟踪系统结构如图2所示。

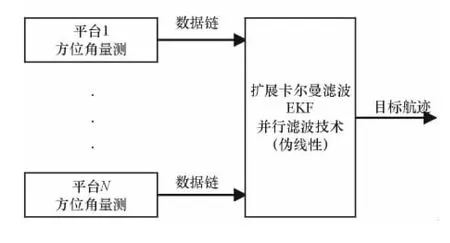
图2 非线性模型跟踪系统结构

2 伪线性模型系统

2.1 目标位置粗估计

被动跟踪示意图如图3所示。设观测平台的位置为Si（xi，yi），i＝1，2，…，N，为平台的个数；θi为观测平 台 对 目 标 量 测 的 方 位 角；T（xt，yt） 为 目标所在航迹上的位置值。方位角θi的真实值可表示成：

式（1）可转换为：

图3 被动跟踪示意图

将式（2）写成矩阵形式：

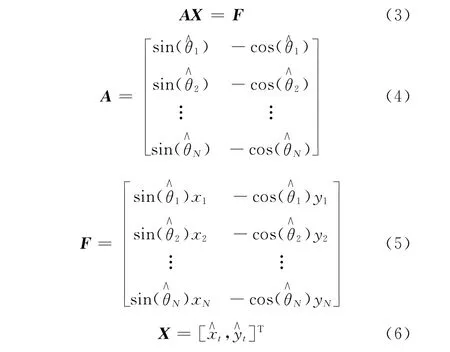
若Δθi为方位角量测噪声，则真实的方位角θi＝i-Δθi。当Δθi为相互独立的高斯白噪声时，式（3）是伪线性形式，若只考虑向量F的噪声干扰，利用最小二乘法可求得目标位置估计值：

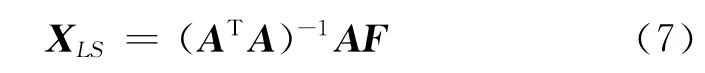
目标位置估计的协方差阵为：

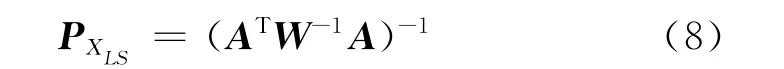
式中：W为量测误差方差，由于文中AX＝F是伪线性的形式，可取W为单位矩阵。

2.2 线性卡尔曼滤波

前面利用观测平台对目标的方位角量测数据，依据静态估计理论最小二乘法估计出某时刻目标的位置值。本节采用卡尔曼滤波对估计的结果进一步处理，从而可以提高精度。

设运动目标的状态方程为：

量测方程表示为：

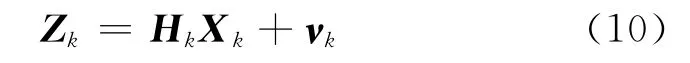
式中：Xk为k时刻运动目标的状态向量；Φk为状态转移矩阵；Zk为量测值；Hk为量测矩阵；ωk和νk分别为状态噪声和观测噪声且假定两者为互不相关的零均值高斯白噪声，其协方差矩阵分别为Qk和Rk。对于上述系统，线性卡尔曼滤波方程表示如下。状态的一步预测及预测协方差：

卡尔曼滤波增益：

在获取新的量测Zk后，滤波更新值及协方差阵：

本文假定目标作匀速运动，采样周期为T，目标的运动状态为X＝ （x，vx，y，vy）T，这时状态转移矩阵为：

将最小二乘法的位置估计值XLS（k）作为卡尔曼滤波中的量测值Zk，估计协方差阵PLS（k）为量测噪声矩阵Rk，这时：

将上述量代入卡尔曼滤波方程，可得到处理后的目标位置。

3 非线性模型系统

设运动目标的状态方程：

式中：νk为均值为0、方差为σ2的高斯白噪声。

将系统线性化处理后，得到扩展卡尔曼滤波的更新值及估计误差的协方差阵为：

其中，扩展卡尔曼滤波的增益为：

式中：Rk为量测噪声协方差矩阵。

4 仿真结果及分析

为验证文中所论述的被动跟踪系统的精度性能，利用Matlab工具设计了仿真试验。仿真场景参数：设2个观测平台所在的位置分别为（-5km，0）和（5km，0），目标以（-10km，10km）为初始位置沿着x轴匀速运动，速度为200m／s。2个观测平台方位角量测噪声均为零均值的高斯白噪声，其标准差分别为0.2°、0.3°，方位角采样周期为1s，蒙特卡罗次数为100次。

在此场景下，观测平台S1、S2位置及运动目标航迹如图4所示，对目标被动跟踪精度如图5所示。

本文选取均方根误差（RMSE）作为被动跟踪精度评价标准。

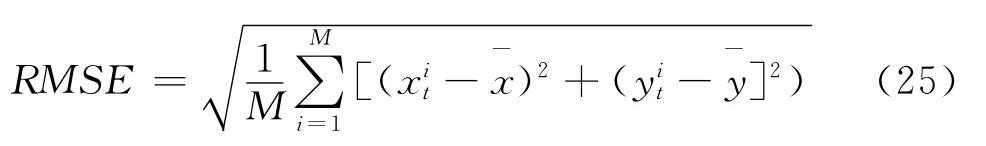
图4 观测平台位置与目标运动航迹

图5 跟踪误差比较

由图5可知：非线性系统对目标的跟踪精度性能比伪线性系统好，而在伪线性系统中，对最小二乘的输出结果进行线性卡尔曼滤波后，很明显提高了目标跟踪精度。

5 结束语

本文针对多平台对单目标的被动跟踪系统，给出伪线性和非线性2种系统结构。伪线性跟踪系统对方位角量测采用最小二乘-卡尔曼滤波相结合的算法进行处理，而非线性系统则基于并行滤波技术对量测数据处理，并在Matlab上进行计算机仿真试验。仿真结果表明，基于EKF的非线性并行滤波技术对目标跟踪精度最高，具有较强的工程应用价值。

［1］ 孙仲康，郭福成，冯道旺.单站无源定位跟踪技术［M］.北京：国防工业出版社，2008.

［2］ 邱玲，沈振康.三维纯角度被动跟踪定位的最小二乘-卡尔曼滤波算法［J］.红外与激光工程，2001，30（2）：83-87.

［3］ 周振，王更辰.机载单站对机动目标无源定位与跟踪［J］.电光与控制，2008，15（3）：60-63.

［4］ 韩崇昭，朱红艳，段战胜.多源信息融合［M］.北京：清华大学出版社，2006.