基于CLEAN算法的HFM脉压信号研究

周旭广，苏 涛，黄 科，张 鹏

（1.西安电子科技大学，西安 710071；2.解放军93856部队，兰州 730060；3.西安陕鼓工程技术有限公司，西安710075；4.解放军93808部队，兰州 730100）

0 引 言

在雷达系统中，脉冲压缩技术较好地解决了雷达探测能力与距离分辨力之间的矛盾，在实际中得到了广泛的应用［1］。相对于线性调频（LFM）信号而言，双曲调频信号（HFM）也具备脉压信号特点。另外，它是一种多普勒不敏感信号，对于运动目标的脉压输出几乎不存在时频耦合的现象。然而，该信号脉压结果的时间宽度较大［2］，且具有较高、缓慢衰减的旁瓣，直接影响了距离分辨力。在多目标环境中，强目标很容易会淹没其邻近弱目标，从而造成目标丢失。在脉冲压缩雷达体制下，为了解决多目标分辨的问题，可以减小发射脉冲宽度或加大信号带宽，但距离旁瓣将会进一步抬高［3］；或者设计更为复杂的相位调制雷达波形［4］，但技术实现会更加困难。

CLEAN算法最初由Högbom于1974年提出，用于改进射电天文中综合孔径合成图的质量［5］。文献［6］利用CLEAN算法对静止目标脉压结果进行处理，实现简单；但该文献并未考虑LFM信号检测运动目标时所面临的问题，即多普勒频移引起的目标距离徙动。为了进一步适应运动目标的检测，本文以HFM信号为雷达发射波形，在分析HFM信号波形特点和多普勒不变性的基础上，首先，使相互邻近的静止或运动目标回波通过匹配滤波器，得到多目标的脉压输出，然后，运用CLEAN算法对脉压结果进行处理。仿真实验表明：本文方法不仅使HFM信号脉压输出的距离分辨力得到了极大提高，而且能较准确地反映运动目标的距离信息。

1 HFM信号模型

1.1 HFM 信号

以双曲调频信号为雷达发射波形，信号表达式为：

式中：A为信号幅度；rect（t／T）为矩形函数；T为脉冲持续时间；μ＝fLfHT／B；f0＝ （fL＋fH）／2，为中心频率，fL和fH分别为信号的频率下限和频率上限，带宽为B＝fH-fL。

由于HFM信号的时宽T和带宽B无相互约束关系，即具有可选择的时宽带宽积，因此该信号能够进行脉冲压缩。由图1可以看出，HFM信号相位曲线是对数函数，其频谱在带宽内拖着长尾递减［7］。

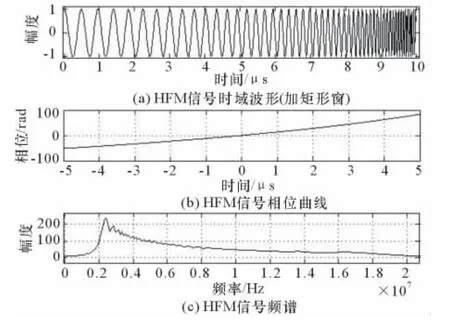
图1 HFM信号的时频特性

1.2 HFM信号多普勒不变性

1.2.1 HFM 信号模糊函数

根据雷达信号模糊函数的定义：

将式（1）代入式（2），利用计算机仿真出 HFM信号的模糊函数。为便于观察，从零多普勒处沿时延轴对三维模糊函数图进行切割，得到半个模糊函数图（见图2）。可知它为近似的矩形脊线，随着多普勒频移的增加，由图3可知，HFM信号模糊函数的脊线几乎与零时延轴保持在同一垂直面上，偏移极小。

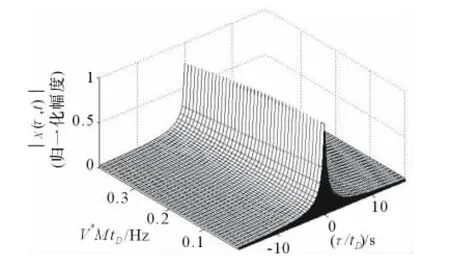
图2 HFM信号模糊函数

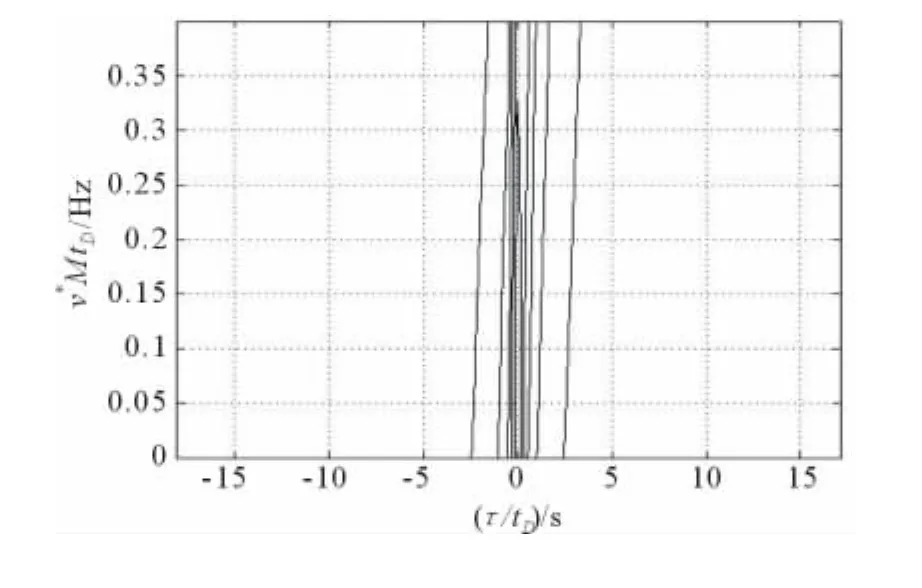
图3 模糊函数对应的等高线图

从图4可知，多普勒失配使得HFM信号模糊函数峰值幅度有所下降，但很缓慢。因此，HFM信号是一种对多普勒极不敏感的信号形式。

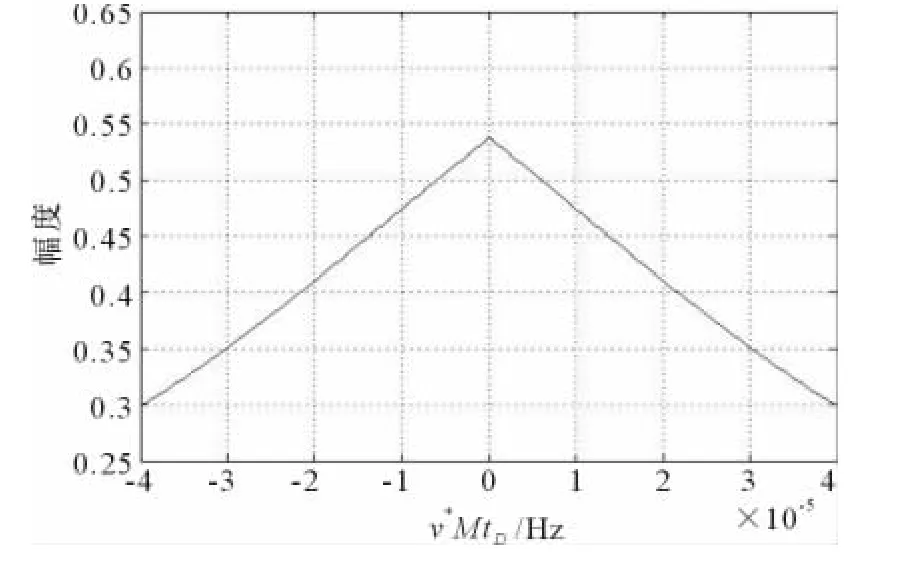
图4 HFM信号零延迟截线

从图5看到HFM信号模糊函数的零多普勒截线时宽大，表明它的距离分辨力较低。

1.2.2 HFM信号多普勒不变性分析

假定雷达发射信号为s（t），R0为目标初始距离，且朝向雷达以匀速v运动，暂不考虑其它因素，则认为目标回波能量不变，归一化之后回波信号表示为［1］：

图5 HFM信号零多普勒截线

令α＝ （c＋v）／（c-v），τ＝2R0／（c＋v），α为多普勒因子，τ为时延因子。

式（3）就是理想条件下目标的回波模型。事实上，当目标静止（即v＝0、α＝1）时，经过时延τ，式（3）与传统回波形式一致，r（t）＝s（t-τ）。可见式（3）是比较严格的回波表达式，对运动和静止目标都具有适应性。

雷达发射HFM信号，经过一定的时延τ，忽略其它因素时，接收机得到的回波为：

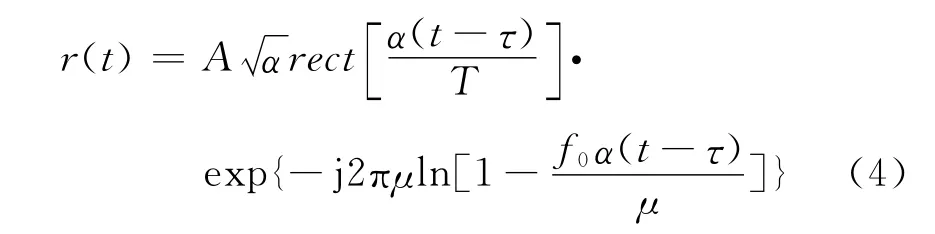
得到回波的瞬时频率：

而发射信号的瞬时频率为：

要使信号满足多普勒不变性，需要找到一个与时间无关的常量td，使得发射信号和回波的瞬时频率满足下式［7］：

代入式（5）和式（6），得到：

明显地，上式中的td是一个与时间无关的量，由此也表明了HFM信号具有多普勒时不变性质，因而它是一类多普勒不敏感信号。

2 基于CLEAN算法的脉压处理流程

CLEAN算法不仅是一种消卷积方法，而且是一个滤波过程，可提高信号脉压分辨力与降低旁瓣［8］。近年来，CLEAN算法在机载毫米波综合孔径成像［9］、空间轨道目标ISAR成像中得到了广泛应用［10］。前人在对SAR成像的处理中，提出在距离向压缩之后进行CLEAN处理。在实际数据运算中，CLEAN算法是对一维数据进行搜索迭代的过程［11］，需要多次将强目标对应的匹配滤波响应找出，依次将强目标的脉压输出进行消除，并预先设定门限值作为退出循环的条件。当剩余脉压结果幅度的最大值小于设置的门限时，循环结束。HFM信号的脉压旁瓣平坦且较高，通过CLEAN算法的逐步消除，可以削弱强目标副瓣和噪声的影响，使得邻近弱目标的主峰显露出来，利于后续的检测。

以HFM信号为雷达发射信号，CLEAN算法的具体流程如图6所示。

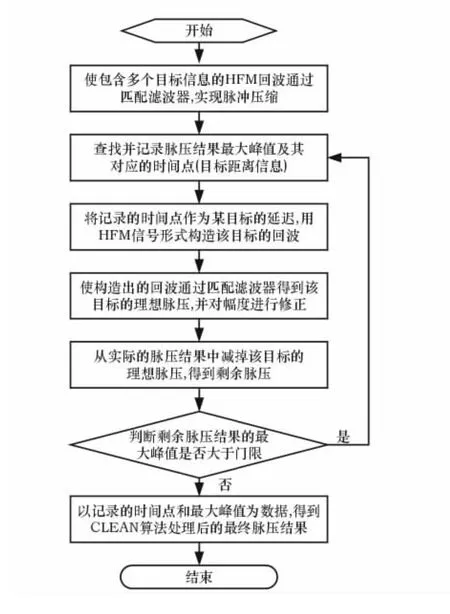
图6 CLEAN算法处理原始脉压结果流程图

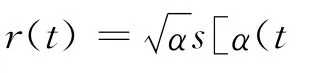
3 仿真结果

3.1 HFM信号的脉压仿真

在Matlab环境下，设目标分别为静止和匀速运动，速度为2倍音速（2Ma），与雷达的距离同为R＝6 000m，雷达发射HFM信号，时宽T＝50μs，频率下限和上限分别为fL＝2MHz和fH＝20MHz，采样频率Fs＝100MHz。由图7可见，尽管2Ma的速度已经非常大，但HFM信号对于运动目标的脉压结果与静止目标相比，差别仍然很小。局部放大图（图8）进一步表明，其脉压输出能够较准确地反映运动目标的距离信息，误差极小，这是其多普勒不变性质的直接表现。同时可以看到，脉压输出虽无明显突出旁瓣，但时宽较宽，较低的距离分辨力不利于邻近多目标的检测。

3.2 CLEAN算法对脉压结果的处理仿真

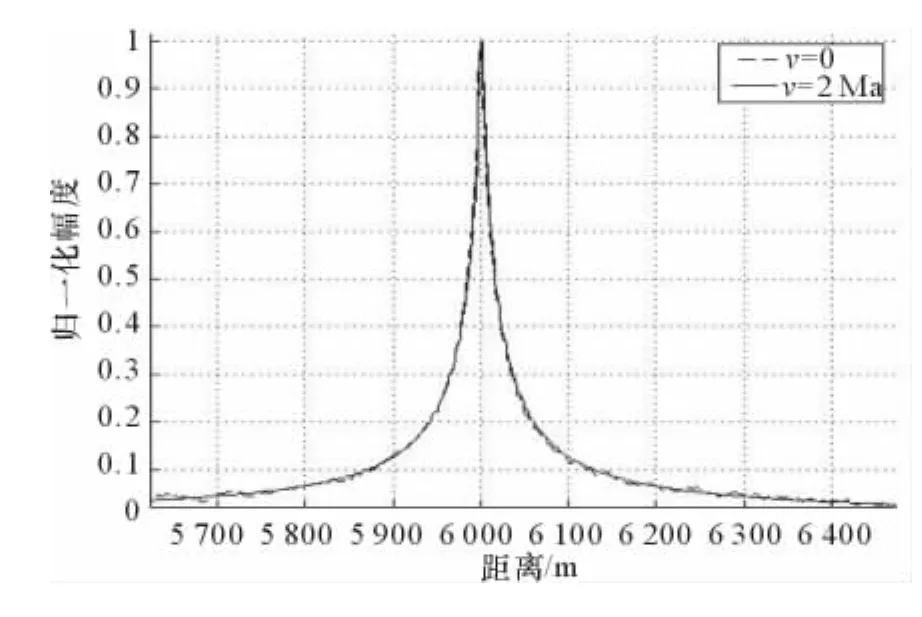
图7 HFM信号脉压结果

图8 脉压结果局部放大

在Matlab中，以HFM为雷达发射信号，设置4个距离相近的静止和运动目标，仿真的部分参数为：距离R＝［9 000m，9 020m，9 050m，9 085m］，雷达有效截面积σRCS＝［3，2，0.8，1.2］，速度v＝［0，0.5Ma，1Ma，2Ma］，门限值设为0.45，均以RCS来表征不同目标的信号强度。目标回波信号未进行脉压之前的波形如图9所示。

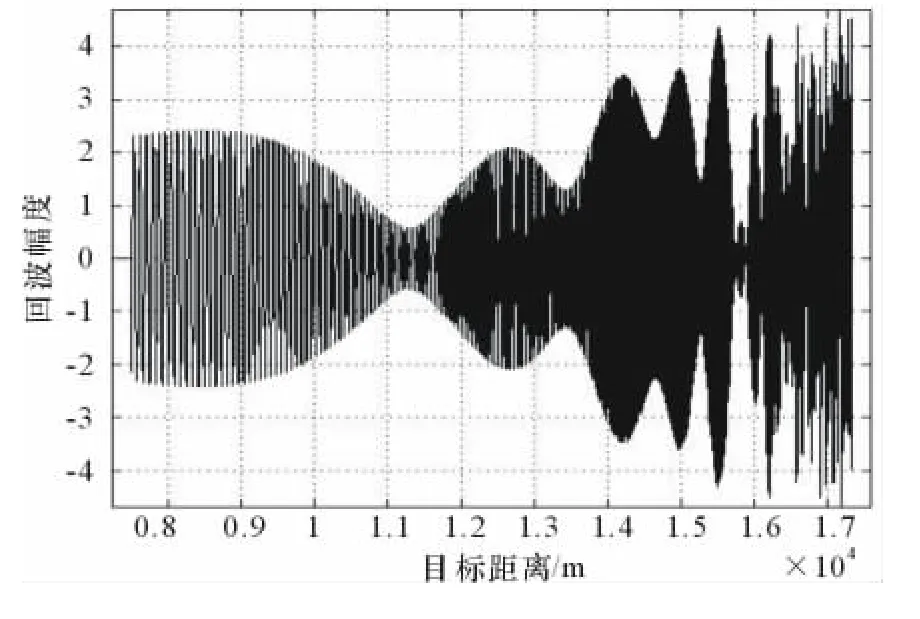
图9 目标回波信号

从原始脉压结果（图10）中可看出，门限值之上只能观察出3个峰值，且不能确定真实目标的具体位置，这表明虽然经过了脉压，但HFM信号并未有效检测出邻近的多个目标。

经过CLEAN算法处理之后（图11），脉压结果将不同速度目标的距离信息准确检测了出来（仿真最大误差不到3m），且具有极高的距离分辨力，消除了旁瓣对主峰的影响。

图10 原始脉压结果

图11 经CLEAN算法处理过的脉压

但同时也应看到，在去除目标的脉压结果中（图12），剩余杂波中仍存在一定数量的突出尖峰，相对高度最高达到了-7.5dB，因此，如果门限选择不当，很容易造成虚警情况的发生。

图12 门限以下的杂波

仿真图中的归一化幅度是以所有目标中最大脉压幅度为标准。

4 结束语

实际中，雷达要探测的目标往往是高速运动的物体。作为一种多普勒不敏感信号，HFM信号对于运动目标的距离检测具有一定的优势。文中对HFM信号的特点进行分析仿真之后，进一步通过CLEAN算法解决了其脉压输出距离分辨力较低的问题。但在CLEAN算法处理脉压结果的流程中，存在2个问题：一是对目标速度的估计需要一定的先验知识，以便更准确地构造目标回波；二是门限值的初始设置要符合实际，否则很容易造成漏警或虚警。因此，速度的预先估计和门限的设定仍待进一步研究。

［1］ 丁鹭飞，耿富录.雷达原理［M］.第3版.西安：西安电子科技大学出版社，2002.

［2］ 朱埜，倪伯林.动物声呐信号在鱼雷中的应用［J］.声学学报，1999，24（1）：29-44.

［3］ 马晓岩，向家彬.雷达信号处理［M］.长沙：湖南科学技术出版社，1999.

［4］ Richards Mark A.雷达信号处理基础［M］.邢孟道，王彤，李真芳译.北京：电子工业出版社，2008.

［5］ Hogbom J A.Apertuer synthesis with a non-regular distribution of interfer-ometer baselines［J］.Astronomy and Astrophysics，1974，15（2）：417-426.

［6］ 陈星，杜雨洺.一种基于匹配滤波的脉压新算法研究［J］.通信技术，2013，46（4）：133-138.

［7］ Yang J，Sarkar T K.Doppler-invariant property of hyperbolic frequency modulated waveforms［J］.Microwave and Optical Technology Letters，2006，48（6）：1174-1179.

［8］ Schwarz U J.Mathematical-statistical description of the iterative beam re-moving technique［J］.Astronomy and Astrophysics，1978，65（2）：345-356.

［9］ 何云涛，江月松，钟宇.CLEAN算法在机载毫米波综合孔径成像中的应用［J］.电子与信息学报，2007，29（7）：1756-1760.

［10］黄小红，邱兆坤，许人灿.空间轨道目标ISAR成像方法［J］.数据采集与处理，2005，20（2）：203-207.

［11］林清源，王彦平，洪文.一种基于CLEAN的SAR图像旁瓣抑制方法［J］.中国科学院研究生院学报，2011，28（5）：355-359.