修正逻辑法在多传感器信息多目标航迹起始中的应用

檀 绪，顾仁财

（中国电子科技集团公司第20研究所，西安 710068）

0 引 言

航迹起始是多目标跟踪技术中的一个重要组成部分［1-5］。任何航迹起始的目的都是希望在目标进入雷达探测区域之后能立即建立起目标的航迹。另一方面，还要防止由于存在不可避免的虚假点迹而建立起虚假航迹。因此，为了确认记录的点迹为可靠航迹，必须花费一定的时间进行确认。换句话说，航迹起始性能是快速起始航迹能力与防止产生虚假航迹能力之间的最佳折衷。由于航迹起始时，目标一般距雷达站很远，传感器探测分辨力低，测量精度差，加之真假目标的出现无真正的统计规律。因此，在多目标航迹处理中，航迹起始是难以处理的问题。其中，杂波环境下多平台多传感器多目标航迹起始更为复杂。在多融合中心的集中式多传感器系统中，不同传感器可能位于不同的平台，传感器的采样周期可能也是不一样的。因此，在进行航迹起始时需要对各传感器来的数据进行时间、空间配准和数据压缩等预处理。

航迹起始是目标跟踪的第一步，它是建立新的目标档案的决策方法，主要包括暂时航迹形成和轨迹确定两个方面，是目标跟踪领域中的首要问题［5］。航迹起始的准则应是在虚警概率最小的情况下能正确起始目标航迹。多目标航迹起始技术具体包括两大类：面向目标的顺序处理技术和面向量测的批处理方法。由于后者在密集杂波环境下计算量太大，工程实现比较困难［4］。

本文采用面向目标的顺序处理技术，重点研究修正逻辑法在多平台多传感器系统中的应用，讨论该航迹起始算法的性能。

1 航迹起始方法

1.1 航迹起始波门的形成

相关波门是用来判断量测值是否源自目标的决策门限，它是以被跟踪目标的预测位置为中心，用来确定该目标下一时刻观测值可能出现范围的一块区域。区域大小由正确接收回波的概率来确定。落入相关波门内的回波称为候选回波。

量测方程为：

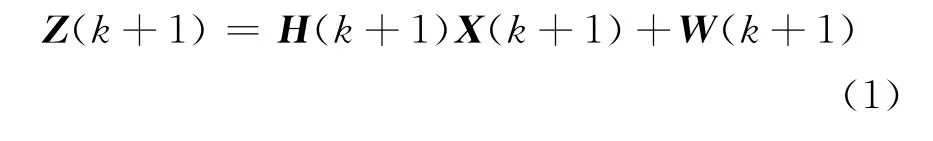
式中：H（k＋1）为量测矩阵；X（k＋1）为状态向量；W（k＋1）为具有协方差R（k＋1）的零均值、白色高斯量测噪声序列。

新息为：

新息协方差为：

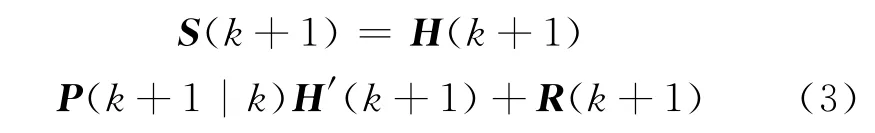
式中：P（k＋1｜k）为协方差的一步预测。

1.1.1 环形波门

环形波门一般是用在航迹起始中的初始波门，它是以航迹头为中心建立的一个自由目标最大、最小运动速度以及采用间隔决定的360°环形大波门。这是由于航迹起始时目标一般距离较远，传感器探测分辨率低，量测精度差，所以初始波门相应地要建大波门，环形波门的内径和外径应满足R1＝VminT、R2＝VmaxT，如图1所示。其中Vmin和Vmax分别为目标的最小和最大速度，T为采样间隔。

图1 环形波门

1.1.2 椭圆（球）跟踪门

若传感器测得的目标直角坐标系下的转换量测值Zc（k＋1）满足：

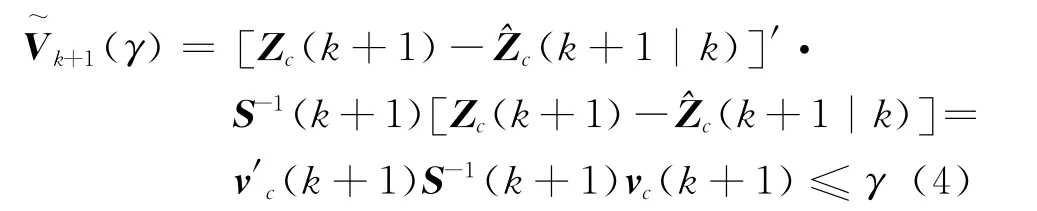
则称转换量测Zc（k＋1）为候选回波，式（4）称为椭圆（球）波门规则。其中参数γ是χ2分布随机变量。当nz＝2时，椭圆相关波门的形状如图2所示。

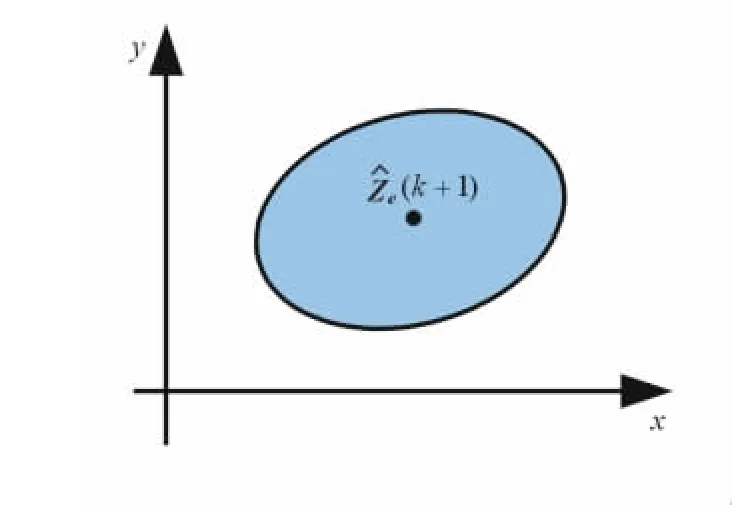
图2 直角坐标系下的椭圆相关波门

对于不同的γ值和不同的量测维数nz，真实量测转换落入波门内的概率PG不同，表1给出了量测维数nz从1到3，不同参数γ对应的概率PG。

表1 nz维量测落入波门内的概率PG

1.2 雷达量测转换

在雷达跟踪系统中，目标的动态模型通常在笛卡尔坐标系中进行建模，而雷达量测一般在极／球坐标系中得到。这时需要将雷达量测通过坐标变换成笛卡尔坐标系量测的伪线性形式，然后估计转换量测误差的前两阶矩。

在球坐标系中，相对于目标的真实斜距r、方位角θ和俯仰角η，雷达量测得到的斜距rm、方位角θm和俯仰角ηm可以定义为：

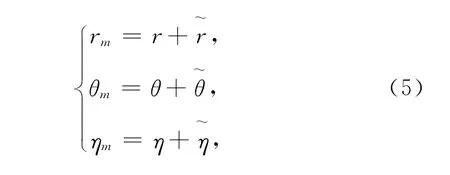
式中：假定斜距量测误差、方位角量测误差和俯仰角量测误差为互相独立、均值为零的Gauss噪声，标准差分别为σr，σm和ση。

式（5）给出的球坐标系中的量测可以通过下式转换成笛卡尔坐标系的量测：

式（6）可进一步写为：

式中：x＝rcosηcosθ，y＝rcosηsinθ，z＝rsinη，（x，y，z）为目标在笛卡尔坐标系中的真实位置。

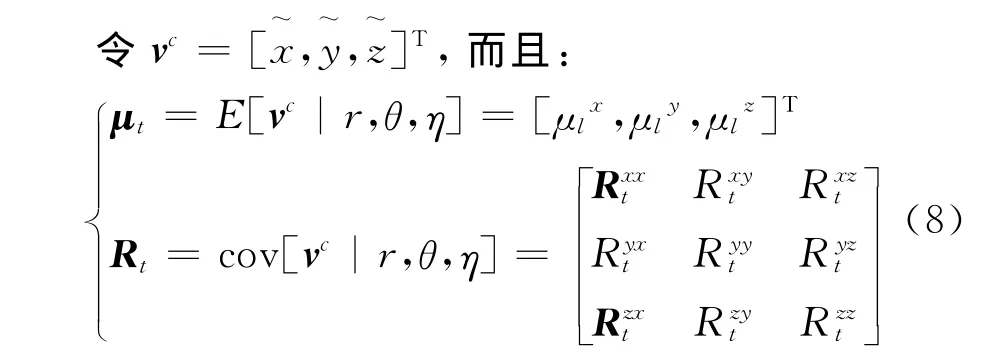
经过推算，真实的偏差和协方差要求已知目标真实的斜距、方位角和俯仰角，但在实际当中，目标的斜距、方位角和俯仰角是无法得到的。为了使其具有实用性，可在量测得到位置 （rm，θm，ηm）已知的条件下对上述真实均值和协方差均值求数学期望，分别为：

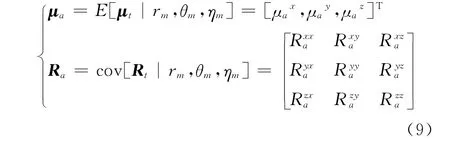
因此，式（6）量测转换修正为：

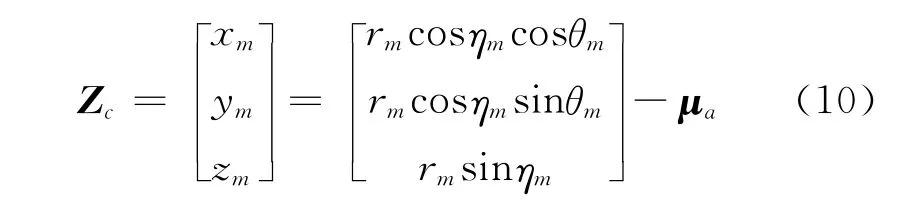
1.3 基于逻辑的航迹起始算法

在多融合中心的集中式数据融合结构中，每个节点上的数据融合处理单元处理来自本地平台和其它远程平台发送过来的所有点迹数据。由于采用相

（2）对每条临时航迹进行直线外推，并以外推点os1为中心，建立后续相关跟踪门。对任意同的数据和融合算法，输出的处理结果也相同。

设ZA（tk）是某一节点接收到的传感器A在tk时刻扫描得到的雷达量测数据（斜距、方位角、俯仰角），对ZA（tk）进行去偏量测转换和空间统一，得到其在融合笛卡尔坐标系下的量测集ZAc（tk），量测对应的协方差矩阵为RAc（tk）。不考虑先扫描到的雷达量测后到达融合中心的情形［5］。

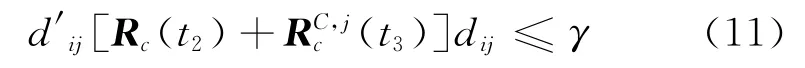
（3）若后续波门没有量测，根据设定的逻辑规则判定是否撤销该临时航迹，如果不撤销，则将该临时航迹进行外推，以外推点为中心建立相关波门，利用式（11）和式（12）来判定第4组到达的扫描量测是否落入跟踪门中。

（4）继续上述步骤，直到形成稳定航迹。

（5）在历次扫描中，未落入相关波门参与数据互联的量测（自由量测）作为新的航迹头，转步骤1。

用逻辑法进行航迹起始时，稳定航迹的确认一般采用滑窗法的m／n逻辑原理，如图4所示。

序列 （z1，z2，…，zi，…，zn）表示含n次雷达扫描的时间窗的输入，如果在第i次扫描时相关波门内有点迹，则元素zi等于1，反之为0。当时间窗口内的检测数达到某一特定值m时，航迹起始便告成功；否则，滑窗右移一次扫描。

图3 航迹起始算法流程图

图4 滑窗法的m／n逻辑原理

1.4 目标状态初始化

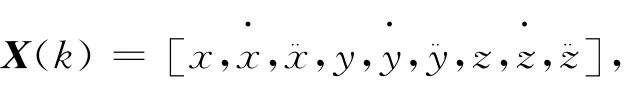
初始协方差阵为：

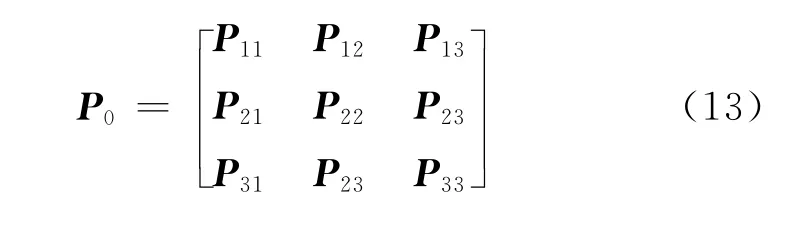
式中：P11、P12、P13、P22、P23、P33为分块矩阵，且：

2 计算机仿真及分析

设一个3D搜索雷达对5个做匀速直线运动的目标进行跟踪，目标初始位置为（80 000m，90 000m，5 000m），（95 000m，70 000m，5 000m），（80 000m，75 000m，5 000m），（85 000m，85 000m，5 000m），（75 000m，60 000m，5 000m），目标运动速度均为（300m／s2，300m／s2，0m／s2）。雷达采样周期为4s，雷达的测距误差、方位角和俯仰角误差分别为σr＝100m，σθ＝0.3°，ση＝0.3°，探测概率为PD＝0.90，杂波均匀分布在雷达视域范围内。

图5显示了雷达探测到的点迹集合，包括杂波和目标真实量测，杂波密度λ＝0.000 1。图6为通过去偏量测转换后的杂波点和真实量测态势图。基于3／4逻辑法起始的航迹如图7所示，从图中可以看出逻辑法能够有效地起始目标的航迹。

图5 雷达探测到的杂波点和真实量测态势图

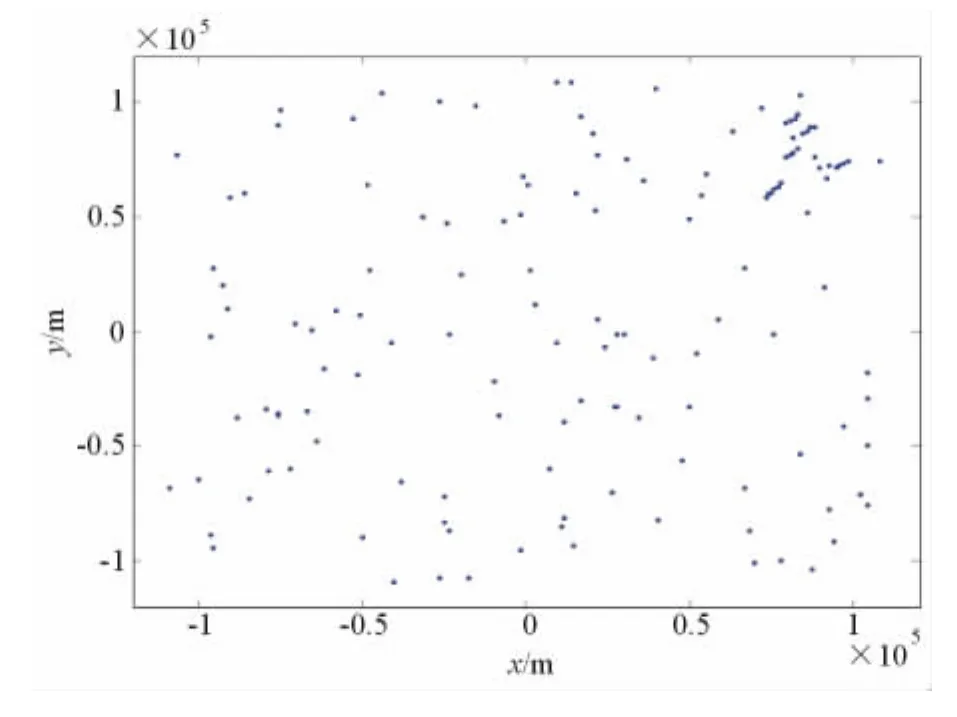
图6 转换到直角坐标系下的杂波点和真实量测态势图

进一步考虑密集杂波环境下的航迹起始问题，杂波密度λ＝0.005。图8为直角坐标系下的杂波点和真实量测态势图。图9和图10分别为基于3／4逻辑法和基于4／5逻辑法起始的航迹图。对比两图可以发现，在密集杂波环境下，3／4逻辑法起始的航迹中存在较多的虚假航迹，而基于4／5逻辑法不仅能够准确地起始目标的航迹，还能有效地抑制虚假航迹的产生。

图7 基于3／4逻辑法起始的航迹图

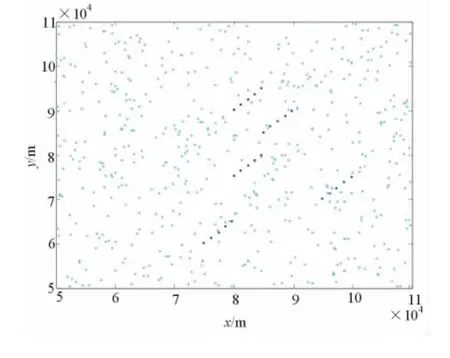
图8 直角坐标系下的杂波点和真实量测态势图

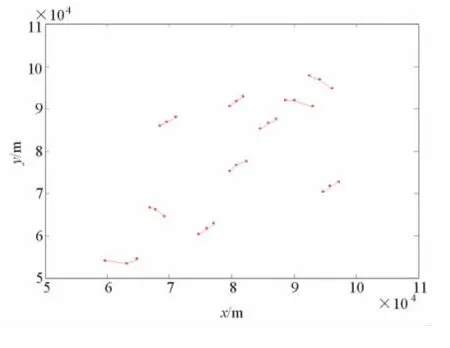
图9 基于3／4逻辑法起始的航迹图

图10 基于4／5逻辑法起始的航迹图

接下来讨论检测概率对航迹起始性能的影响。取杂波密度λ＝0.005，检测概率PD＝0.70。

图11为直角坐标系下的杂波点和真实量测态势图。图12和图13分别为基于3／4逻辑法和基于3／5逻辑法起始的航迹图。

图11 直角坐标系下的杂波点和真实量测态势图

图12 基于3／4逻辑法起始的航迹图

图13 基于3／5逻辑法起始的航迹图

对比图12和图13可以发现，在相同杂波环境和检测概率下，3／4逻辑法起始的虚假航迹较少，但也不能有效地起始真实目标的航迹；基于3／5逻辑法产生了较多的虚假航迹，但却保证了更高的真实目标航迹起始概率。

3 结束语

本文研究了密集杂波环境下多目标航迹起始问题，分析并采用了面向目标的顺序处理技术，讨论了算法存在的不足。为了在复杂杂波环境下得到比较好的航迹起始结果，重点研究修正逻辑法在多平台多传感器系统中的应用，最终讨论该航迹起始算法的性能。该算法能够较有效的完成多个目标的起始。最后通过计算机仿真，仿真了算法流程并分析了在不同参数下修正逻辑法对航迹起始的正确率。

［1］ Bar-Shalom Y，Fortmann T E.Tracking and Data Association［M］.Walpham：Academic Press，1988.

［2］ Bar-Shalom Y，Li X R.Multitarget-Multisensor Tracking：Principles and Techniques［M］.Storrs，CT：YBS Publishing，1995.

［3］ 何友，关欣，王国宏.多传感器信息融合及应用［M］.北京：电子工业出版社，2007.

［4］ 朱洪艳，韩崇昭.航迹起始算法研究［J］.航空学报，2004，25（3）：284-288.

［5］ 苏峰，王国宏，何友.修正逻辑航迹起始算法［J］.现代防御技术，2004，32（5）：445-456.