相位量化DRFM的误差性能分析

吕东泽，喻旭伟，何 敏

（中国电子科技集团第29研究所，成都 610036）

0 引 言

数字射频存储器（DRFM）可以产生与雷达信号相干的干扰信号，对采用多普勒、脉冲压缩等技术的相干雷达具有很好的干扰效果，因此DRFM在电子对抗领域得到了广泛的关注［1］。DRFM按照其量化方法分为幅度量化DRFM和相位量化DRFM。其中相位量化DRFM具有结构实现简单、存储量小、动态范围大等优点，相比幅度量化，DRFM还具有可以直接进行频率和相位调制的优势［23］。

在相位量化DRFM系统中，针对威胁雷达信号的瞬时相位信息进行量化然后进行存储、调制等处理，相位量化DRFM主要分为1bit、3bit和4bit相位量化DRFM［4-6］。由于量化位数有限且雷达信号存在噪声，因此存储的瞬时相位信息存在量化误差和噪声误差，这就会影响相位量化DRFM的性能。因此，本文对噪声环境下相位量化DRFM的量化和噪声相位误差进行了研究，并对其统计特性进行分析。

1 相位量化DRFM

图中比较器输出为4bit数据流I0＝sgn ［cosφ］，I1＝sgn ［cosφ-45°］，I0＝sgn ［sinφ］，I1＝sgn ［cosφ＋45°］［9］。利用编码器可以将比较器输出的4bit数据流变换为3bit编码数据流，由

1.1 相位量化DRFM结构

相位量化DRFM是根据威胁雷达信号瞬时相位的不同而对信号的2π相位进行量化的，当量化位数为m时，将其划分为2π／2m个相位子空间［7-8］。3bit相位量化DRFM的结构如图1所示。于格雷码具有良好的纠错特性，因此本文采用格雷 码，该编码器的输入与输出变换关系如表1所示。

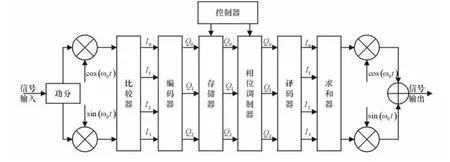
图1 3bit相位量化DRFM结构图

表1_编码器输入与输出变换关系

1.2 相位DRFM信号模型

相位DRFM接收到的威胁雷达信号为：

式中：A为幅度；f0为频率；φ为信号相位。

对接收到的雷达信号进行采样后可表示为：

将样本点数取为N0＝p·N，其中p为样本中包含的被测信号周期数，N表示每周期点数，对信号进行整数周期采样，则正交变换后I支路信号表示为：

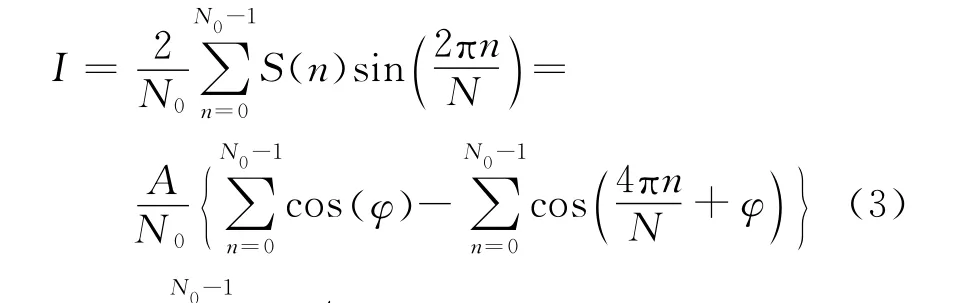
同理可得正交变换后Q支路信号为：

因此相位的计算公式为（-π≤φ≤π）：

2 相位量化DRFM中噪声及量化误差分析

2.1 量化误差、噪声误差分析

同时考虑到量化噪声和高斯白噪声时，相位DRFM接收的威胁雷达信号可以表示为：

式中：el（n）为量化噪声；eg（n）为高斯白噪声。考虑到噪声后的Q支路信号表示为：

式中：Qg，Ql分别为高斯噪声以及量化噪声经过正交变换后的值，并有：

将相位DRFM的量化噪声el（n）看作均匀分布的噪声，则其量化间距Δ为：

式中：m为量化位数。

则el（n）以等概率分布在 （-Δ／2，Δ／2）的区间内，有E（el（n））＝0，σ2el＝Δ2／12。因此可知信号每一个采样点的量化误差是期望为0、方差为Δ2／12的均匀分布，且它们相互独立，则有：

式中：σ2Ql为随机变量Ql的方差。

设高斯白噪声eg（n）是均值为0、方差为σ2g的随机变量，可知：

式中：σ2Qg为随机变量Qg的方差。

令误差项Qe＝Qg＋Ql，根据概率论计算Q的过程中，噪声经过变换服从高斯分布，其均值为0，又有Qg，Ql相互独立，则其方差为：

将式（4）和式（5）代入式（15）可得：

已知接收信号的信噪比SNR＝A2／σ2g，并将N0＝pN代入可得：

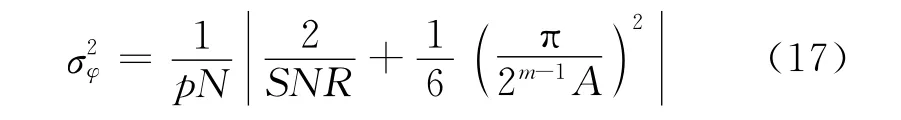
2.2 DRFM量化后相位噪声的统计特性

叠加在I，Q两支路上的噪声Qe，Ie均服从零均值高斯分布，方差为2σ2g／N0。在I≥0时，相位估计值与真实值之间的误差为：

式中：φe为相位误差；φ′为相位的估计值；φ为相位的真值。

则相位误差的概率分布函数为：

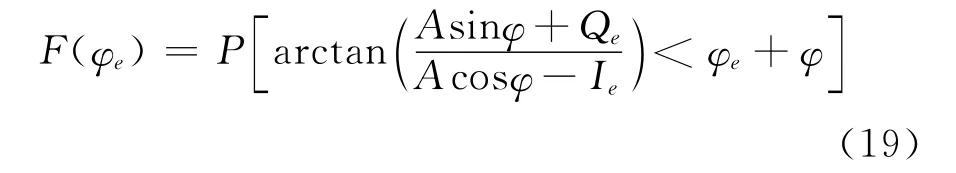
已知相位0≤φ（t）≤π／2，则arctan函数为单调递增，因此有：

假定Qe，Ie的联合概率密度函数为f（Qe，Ie），则相位误差的概率分布函数为：

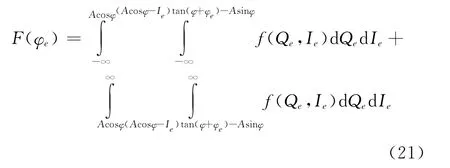
对相位误差的概率分布函数求微分即可得到相位误差的概率密度函数：

已知Qe，Ie 服从均值为0、方差为σ2 ＝2σ2g／N0＋Δ2／6(N0) 的高斯分布，因此有：

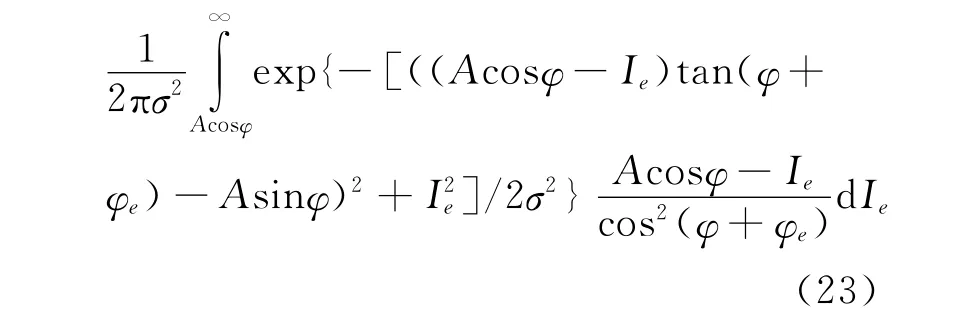
由上式可知，相位误差的概率密度函数与瞬时相位真实值有关，并且具有复杂积分形式，实际应用中可依据上式对相位误差的概率分布进行估计和分析。

3 仿真分析

采用3bit相位DRFM，此时分别在接收到的雷达信号不存在高斯白噪声、SNR＝30dB和SNR＝10dB的情况下进行仿真，3种情况下DRFM接收的原始信号和3bit相位量化后的相位值分别如图2～4所示。由图可见，不存在高斯白噪声时，量化后的相位值与真实值最逼近；存在高斯白噪声时，随着信噪比的降低，信号进行相位量化后的相位误差增大。

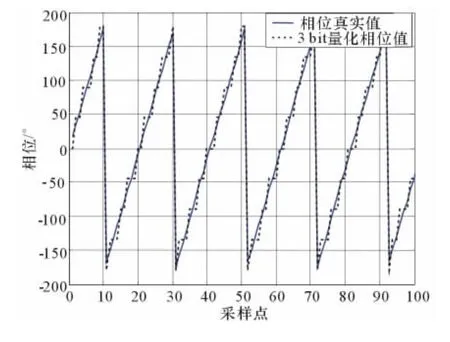
图2 3bit相位量化前后相位值

图3 SNR＝30dB，3bit相位量化前后相位值

不存在高斯白噪声时3bit相位量化后的误差概率密度函数如图5所示，此时仅存在量化误差，量化误差服从均匀分布。雷达信号信噪比在30dB～0dB时，其3bit相位量化后的误差概率密度函数如图6所示。由图6可见该误差分布较为复杂，在信噪比较高即噪声功率较小时，其相位误差较小，此时可以对相位进行校正从而使相位DRFM具备较好的相干性；在信噪比较低即噪声功率较大时，其相

图4 SNR＝10dB，3bit相位量化前后相位值

位误差较大，此时难以对其相位值进行校正，相位DRFM的相干性较差。

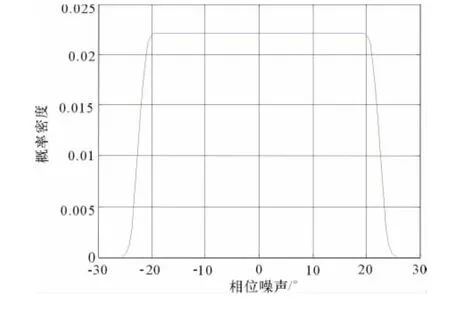
图5 相位DRFM量化误差概率密度函数

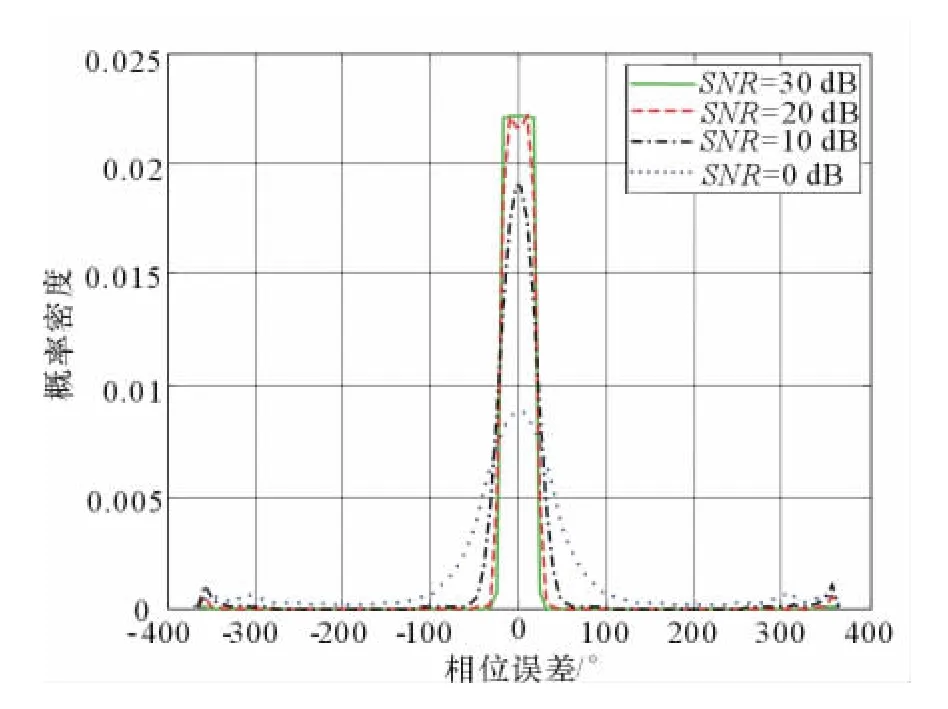
图6 不同SNR时误差概率密度函数

4 结束语

本文对相位量化DRFM的误差性能进行分析，结果表明：

（1）相位量化DRFM系统中由于量化位数有限从而在量化过程中产生误差，该量化误差服从均匀分布；

（2）雷达信号中存在高斯白噪声时，对信号量化后的相位误差包括量化误差和噪声误差两部分，该相位误差的概率密度函数为与瞬时相位真实值有关的复杂积分形式；

（3）随着雷达信号信噪比的降低，相位量化后的相位误差增大，相位DRFM的相干性降低。

［1］ Schleher D C.Electronic Warefare in The Information Age［M］.Boston：Artech House，2000.

［2］ 王春丽，安红.多比特相位量化仿真技术及应用研究［J］.航天电子对抗，2009，25（3）：61-64.

［3］ Neri F.Introduction to Electronic Defense Systems［M］.Perth：Sci Tech Pulishing，2006.

［4］ 喻旭伟.3bit相位量化技术［J］.电子对抗技术，2001，16（5）：28-31.

［5］ 曲尔光.数字射频存储器多比特相位量化原理及影响寄生电平的因素［J］.山西大学学报（自然科学版），2002，25（1）：34-37.

［6］ 苏培勇，唐斌.数字储频的结构及其比较［J］.舰船电子对抗，2005，28（6）：30-32.

［7］ Vu T T，Hattis J M.A GaAs phase digitizing and summing system for microwave signal storage ［J］.IEEE Journal of Solid-State Circuits，1989，24（1）：104-117.

［8］ 周国富.相位量化DRFM 性能分析［J］.电子学报，2005，33（12）：2213-2218.

［9］ 周国富，姬国良.相位量化数字射频存储器的设计考虑［J］.系统工程与电子技术，1994（2）：27-31.

［10］李滔，李勇.基于正交变换的相位估计方法性能分析［J］.电子与信息学报，2008，30（8）：1857-1860.