一种基于数据平滑技术的回归预测算法

龙浩，霍娜

（徐州工业职业技术学院 信息管理技术学院，江苏 徐州 221000）

一种基于数据平滑技术的回归预测算法

龙浩1，霍娜2

（徐州工业职业技术学院 信息管理技术学院，江苏 徐州 221000）

在基于固定窗口宽度滑动窗口模型的基础上，提出了一种基于回归参数存储的预测模型，该模型设置了计算区、数据区和参数区。计算区用于获得最近一个滑动窗口中的数据，数据区用于接收新数据，参数区存储最近若干组滑动窗口数据所计算得到的线性回归参数值，作为计算预测结果的原始数据集。按照这种模型的处理思路，提出了一种基于数据平滑技术的回归预测算法，随着窗口的滑动，对数据区中的数据进行回归分析，获得前面若干组滑动窗口数据的回归函数并存入参数区中，检验当前窗口中数据获得的回归函数预测效果。实验分析表明，通过修正当前回归函数的参数，可以使预测函数的预测精度得到很大程度的提高。

数据流；预测模型；数据平滑技术；回归预测算法

0 引言

数据流预测，是通过对数据流建立预测模型，分析既有的数据，利用不同的分析方法，对其将来的趋势进行预测。这对于灾害的防控有重要的意义，可以通过对某段时间的数据流分析，预测出可能发生的灾害，从而消除隐患，达到防患于未然的目的。目前，国内外现有的研究工作主要集中在数据流的局域实时信息查询和压缩处理方面，但是对数据流变化趋势的预测查询较少。由于数据流模型有其独特的性质：实时和独立，因此，基于数据流的预测技术，其预测速度会显著提高，又因其系统环境和人为干预的影响因素少，也使得预测结果更加准确[1]。

根据数据流的定义——数据流是实时、连续、有序的数据项序列（顺序由到达时间隐含地表示或显式地由时间戳指定），数据流的数量在理论上是无限的，无法完整地存储下来。关于数据流可以找出如下关键词：实时，连续，有序，数量无限。由于数据流应用环境的这些特点，对我们的预测查询提出了相应的要求[2]。

首先，数据流预测查询的目标是为实际的应用提供有效的信息预测服务，因此，根据当前获取的信息，数据流预测查询算法应该有较高的预测精度，对于在未来的时间段内的发展趋势应该有较为精确的预测和估算。

其次，数据流是实时变化的数据序列，因此，数据流预测查询应该有较快的实时响应速度，在用户可以接受的时间范围内，预测算法应该有比较优秀的时间复杂度[3]。

最后，数据流应用环境的数据量非常庞大，这就对计算机的内存带来了巨大的压力，因此，数据流预测算法必须在保证预测精度的基础上，采取多种方法降低对内存的压力，从而提高预测效率。

在运用回归分析方法分析事物发展变化趋势时，必须找到影响预测目标变化的主要因素，才能建立预测模型。选取单因素条件下的回归预测，即仅考虑现场监测数据基于时间因素t的变化函数f（t）。根据目前观测到的数据集，采用回归分析方法，计算得到关于数据流的变化函数。

1 基于数据平滑技术的回归预测模型

在数据流环境中，数据具有变化连续、无限、快速的特点，在这种情形下对数据流进行预测，要达到预设的要求和理想的效果比较困难[4-5]。文中提出了一种基于数据平滑技术的回归预测模型（如图1所示），该模型设置了三个缓冲区，计算区用于获得最近一个滑动窗口中的数据，参数区用于存储基于最近若干组（设为m组）滑动窗口数据所计算得到的若干组线性回归参数（a，b）的值。模型中的滑动窗口是基于固定窗宽的滑动窗口，它保留最近到达的n组数据，n称为滑动窗口的窗宽。在模型中，滑动窗口可以看作是一块内存缓冲区，新到达的数据进入这个缓冲区，当新数据填充该滑动窗口的内存区域时，计算区中的数据被清空，然后将滑动窗口内的数据移到计算区中，滑动窗口继续获取新的数据。

随着窗口的滑动，对计算区中的数据进行回归分析，获得针对若干次滑动窗口中数据的回归函数并存入参数区中，检验基于计算区数据计算得到的回归函数的预测效果。如果预测效果不理想，通过修正当前回归函数的参数，可以有效地提高预测函数的预测精度。

图1表明了预测模型的一次处理过程。首先通过当前计算区中的数据计算出回归函数f（a2，b2），接着通过该函数预测当前滑动窗口上的值，比较预测值与实际观察值的偏差。如果预测效果达不到设定要求，修正回归函数参数，用参数区中的函数参数集（a0，b0），（a1，b1）修正当前的函数参数（a2，b2），得到修正后的预测函数f（），然后判断新函数f（）在当前滑动窗口上的预测效果，可以反复修改参数，直到预测效果满足给定条件为止。参数修正的时间必须小于一个滑动窗口的更新周期Δt，在一个更新周期Δt内，预测函数的预测效果如果无法满足用户设定的条件，则更新计算区和参数区中的数据，算法重复执行。

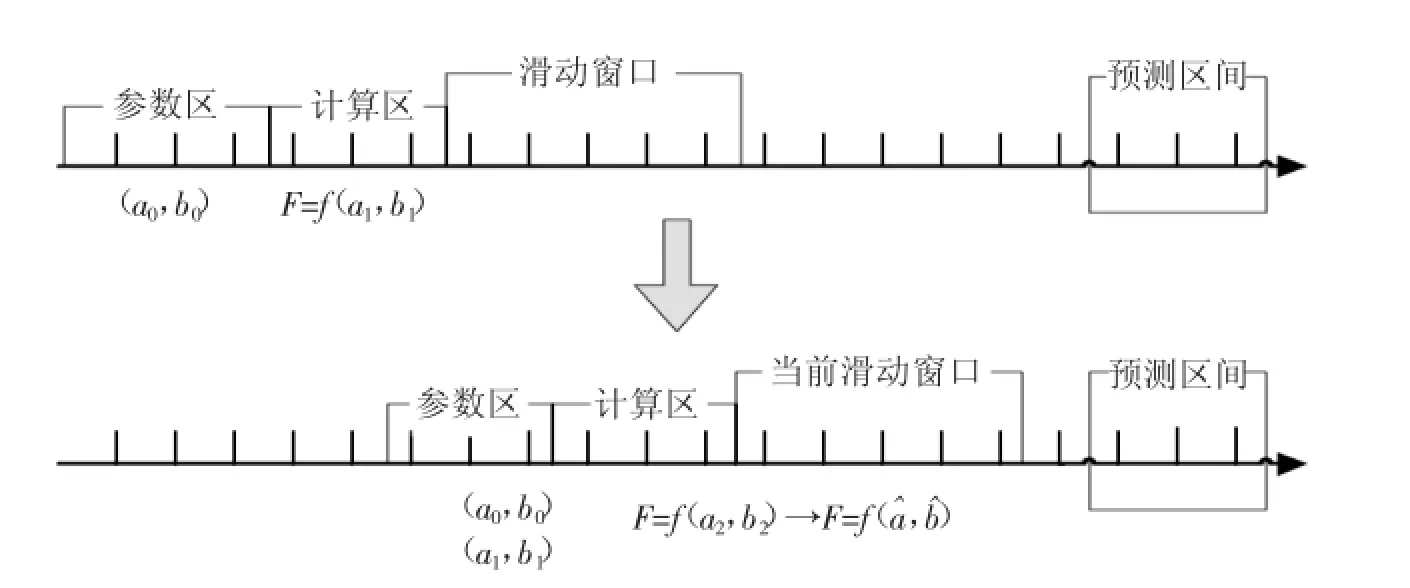
图1 回归参数存储的预测模型

2 算法描述

该算法分为4个阶段。

第1阶段：用数据缓冲区中最新得到的数据，建立线性回归方程，这里是回归方程的系数。

第2阶段：根据第一阶段得到的回归函数，计算在预测区间上的预测值，并与实际观察值比较，计算预测的残差。

第3阶段：比较计算得到的残差和用户给定的阈值σ，判断残差是否大于σ，“是”则说明预测失败，转第4阶段，“否”则说明接受预测函数。

第4阶段：根据一个窗口时间的大小，给定阈值n，判断预测失败的次数的累加值和阈值n的大小，失败次数小于n则转入参数调整策略，否则更新数据缓冲区中的数据，转第1阶段重新执行。

算法的说明如下：

输入：预测函数y=f（x）+β，滑动窗口获取的数值（y0，y1，…，y∞），需要预测的时间区间（tj，tj+1，…，tj+n-1），j∈（0，∞）用户可接受的精度阀值θ

算法中函数的具体说明：

LRA（yi，yi+1…yi+n-1）表示对窗口（yi，yi+1…yi+n-1）中烟流温度值（即火灾中产生烟流的温度值）进行线性回归分析，得到参数a，b的估计值；

GET_RSS（f_yk）：计算窗口（tj，tj+1…tj+n-1）（j＞I）对应（yj，yj+1…yj+n-1）的残差；

ADJUST（f-a，f-b）表示根据当前窗口数据的变化趋势，调整预测函数参数取值，调整策略采用指数平滑法。

ACCEPT（adj_c）表示以合适的形式输出符合精度要求的烟流温度值。

3 实验结果分析

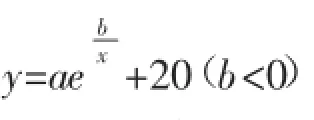
表1 FDS4.0火灾模拟现场数据流

窗口宽度选取500，根据20 000条数据对未来（900～1 200）（1 200～1 500）（1 500～1 800）（1 800～2 100）（2 100～2 400）（2 400～2 700）（2 700～3 000）（3 000～3 300）（3 300～3 600）几个时间段内的烟流温度值进行预测，显示参数进行指数平滑前后对预测精度的影响。实验从600～900条数据开始，根据600～900条数据计算得到的a，b（3.541，-99.08），平滑系数选取前次窗口的调整值0.65，预测精度变化如图2所示。横坐标表示预测的时间段，纵坐标表示预测精度，精度用残差RSS表示。从图中可以看出，靠近样本窗口的数据，使用未经过平滑处理的参数获取的温度估计值精度较高，但要预测远离样本窗口的温度值时，平滑处理后的参数值会获取较高精度的温度估计值。

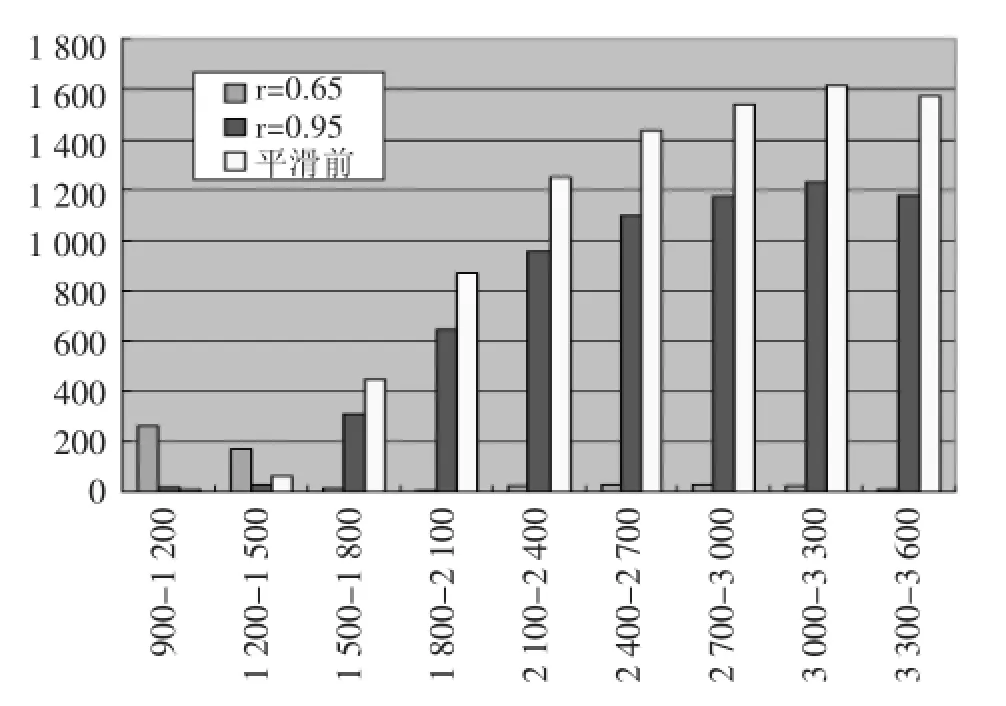
图2 指数平滑法平滑效果比较图

4 结论

实验证明，通过回归参数存储的预测模型，随着窗口的滑动，对数据区中的数据进行回归分析，获得前面若干组滑动窗口数据的回归函数并存入参数区中，用来检验当前窗口中数据获得的回归函数预测效果，如果效果不理想，通过修改回归函数的参数，可以有效提高预测函数的预测精度。

［1］Vazhkudai S，Schopf J M.Using regression techniques to predictlarge datatransfers［J］.International Journal of High Performance Computing Applications，2013，17（3）：249-268.

［2］李建中，郭龙江，张冬冬，等.数据流上的预测聚集查询处理算法［J］.软件学报，2010，16（7）：1252-1261.

［3］李国徽，陈辉，杨兵，等.基于概率模型的数据流预测查询算法［J］.计算机科学2012（4）.

［4］李国徽，付沛，陈辉，等.基于GEP方法的数据流预测模型［J］.计算机工程，2013.

［5］陈安龙，唐常杰，傅彦，等.基于能量和频繁模式的数据流预测查询算法［J］.软件学报，2008（6）.

Data Stream Pred iction Model Based on Parameters Smoothing Methods

LONG Hao1，HUO Na2
（Information Management Institute,Xuzhou College of Industrial Technology,Jiangsu Xuzhou 221000,China）

Fixed windowwidth model meansthe size ofthe sliding windowwidth is afixed number.Based onthis model，this paper proposed adatastreamprediction model based on regression parameters smoothing method.Compared withthe sliding windowmodel，anewbuffer zone is set forthe storage ofthe parameters which calculated by recent data.Then anewdatastreamprediction algorithmis proposed.By usingthe datain current databuffertogetthe prediction function，we can getthe prediction value in current window.Given afixed deviation value，ifthe difference betweenthe prediction results and observation datanotlessthanthe deviation，parameters correction stepneedtobe done，in whichthe prediction function parameters needtobe changed.Experiments showusthatthis algorithmcan reducethe space andtime complexity，and alsoimprovesthe prediction accuracy.

datastream;prediction model;sliding window; regression parameters

TP309．1

A

1673-2022（2014）04-0047-04

2014－08－26

龙浩（1984-），男，湖南长沙人，讲师,主要研究方向为软件工程、数据挖掘；霍娜(1984-)，女，陕西榆林人，讲师，主要研究方向为软件工程。