汾西TFC6905-3型发电机的机体模态分析

卢五弟，林建中，陈云

（1.上海理工大学，上海200090;2.瓦锡兰中国有限公司，上海201201; 3.上海安声船舶技术有限公司，上海 200333）

安装在大型柴油机组上的发电机，工作运行时受到发动机不同频率下的激励，使其结构产生振动、变形，甚至产生共振，对整个机组结构强度造成一定破坏，甚至影响整个机组的安全工作性能.目前工程应用中，使用有限元分析法对发电机进行模态分析，是最为快速有效的方法，能解决复杂的机构设计问题，其精确性和正确性是国内外专家学者研究的重点;［1］而基于发动机的激励源来调整发电机的结构参数的分析方法，更是减振、降噪设计中需要考虑的重点方向.［2］

模态分析法是对运动机构的动态性能分析，通过该方法得到结构体完整的模态参数，建立起结构动态响应动力学模型，对其动态性能作研究分析，调整结构参数，为其强度设计和动态特性分析提供依据.［3］

本文采用有限元模态分析法计算了发电机体的固有频率及其振型，主要包含自由无约束状态下的模态分析和约束状态下的模态分析，根据发动机的激励来研究分析在0～200 Hz频率段内的其前15阶模态振型及其固有频率.［4］

1 创建几何模型及FEM分析

利用ABAQUS/CAE 6.12.3/ANSYS V12有限分析计算软件建立某型发电机机体的有限元模型，确定设计结构或机体的振动特性（固有频率和振型），为完成振动模态实验和优化模型设计参数提供参考.主要模态计算分析法包含自由状态下的模态分析和约束条件下的模态分析，由于其匹配的为瓦锡兰公司的中速柴油机，额定转速为720 r/min或750 r/min，根据发动机的主要激励，分析结果包括0～200 Hz频率的前15阶模态计算结果.

在ANSYS V12中采用三维实体单元建立机体实体模型，将模型导入ABAQUS/CAE 6.12.3有限元软件中进行网格划分和求解，采用两种特征值提取方法，即Lanczos方法和子空间迭代算法.提取多阶频率时，使用Lanczos方法提取速度快;提取的模态阶数少于20阶时，使用子空间迭代法更快，使用位移作归一化处理，得到各阶振型的最大位移量.通过脉冲响应函数进行特征系统实现算法（ERA），除了可得到模态频率、阻尼和振型等参数外，还可得到模态质量和刚度.当模态频率较密集、频域识别有难度时，将频响函数逆变换得脉冲响应函数，用ERA方法进行识别，可得到满意的结果.

有限元分析过程包括前处理、施加载荷求解和后处理3个环节.前处理包括分析环境设置、定义单元机材料类型、建立几何模型、网格划分、定义边界条件和约束条件等.施加载荷和求解包括定义载荷信息、指定分析类型和分析选项、执行求解等.后处理则包括对求解结果的各种统计和计算，如绘制矢量图、云图、观察指定位置的数值等操作.

计算的方法主要采用Lanczos分块方法和基于SIM的线性动态分析法.模型定义的主要参数如下.

（1）单位参数：长度（mm），重量（t），时间（s），力（N）.

（2）坐标参数：X-轴，Y-轴，Z-轴.

（3）材料参数：材料名称为Q 235 A（GB/T 3274—2007），质量密度为7 850 kg/m3，杨氏模量E为200 GPa，泊松比为0.3.

FEM方法计算满足如下条件：

（1）3D模型导入ABAQUS/CAE 6.12.3分析软件;

（2）分析过程中忽略模型结构的小台阶;

（3）所有的网格化基于局部水平，用10节4立方体C3D10元素法;

（4）实体均匀截面，材料同为Q 235 A;

（5）模型网格元素的尺寸均为40 mm，模型以有限元网格划分;

（6）自由状态下前15阶最小固有频率的模态分析;

（7）约束条件下，通过固定电机地脚3个螺栓来约束所有自由度（DOF），并对前15阶最小固有频率的模态进行分析;

（8）仅研究频率0～100 Hz间的模态振型.

FEM模型的质量参数要求如下：

（1）最小面贴合角大于3°;

（2）最大面贴合角小于170°;

（3）纵横比小于10°;

（4）分析误差为0%;

（5）分析预警小于4%.

模型的基本信息如下.

（1）经收敛性验证后，网格元素定义为193 938.

（2）网格节点为381 837.

（3）有限元模型的总质量为2.862 t.

（4）重心位置为－0.000 644 994 21（X），14.203 43（Y），－1 096.332（Z）.

（5）原点转动惯性矩Ixx=6 307 980;Iyy= 6 575 178;Izz=1 450 372.其约束条件为：约束电机的上、下平面，通过固定电机地脚3个螺栓来约束所有自由度（DOF）.

2 计算结果与分析

根据FEM模态计算结果可以获得自由状态下和约束状态下的固有频率和振型的分析结果，如表1所示.

由表1可知，在自由状态下前6阶为刚体模态，此时机体外形不发生变化，并在相应频率下作转动或平移运动;当第7阶机体将开始发生弹性体变形时，最小频率为41.39 Hz，并作1阶扭转.在自由状态下的机体的固有频率和振型如图1所示.当在约束状态下的1阶模态时，机体就开始发生弹性体变形，最小频率为43.27 Hz，并作1阶轴向弯曲.约束状态下的机体的固有频率和振型如图2所示.

表1 自由状态和约束状态下发电机机体的固有频率和振型

图1 自由状态下机体的固有频率和振型

图2 约束状态下机体的固有频率和振型

两种状态下发生弹性体模态的最小频率误差率为4.5%，这是由于边界的约束条件不同，导致振型不同.由图1和图2分析可知，机体两端的端板刚度较小，振幅较大，因此需要调整结构参数，改进结构设计，提高其强度.

3 模态试验分析法

采用锤激法对已有相同型号的发电机的机体作模态试验，采用OROS RX35型8通道分析仪，结合Kistler8762A50三轴向传感器，并采用逐点采集法，采集点位于发电机的机体，利用ME Scope VES 8.20分析软件进行分析，其结果如图3所示.

通过模态试验分析可知，试验的结果和在自由状态下的计算结果相近，当机体处于弹性模态时（40～100 Hz频段）各阶固有频率的误差约为1 Hz，验证了自由状态比约束状态下的有限元仿真分析更具有参考价值.

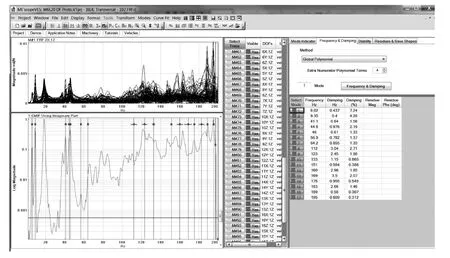
图3 对已有相同型号的发电机机体进行模态试验分析界面

4 结语

对转速为720 r/min或750 r/min的中速柴油发动机，主要研究其频段为25～100 Hz间的弹性体模态的固有频率和模态振型，若避免发动机的激励与发电机的固有频率相重合而发生共振现象，必须提高该机体的弹性体模态的最小固有频率至60 Hz.（假设发动机生产商最大缸数为9 L或18 V型，根据发动机激励可以计算发火频率为56 Hz.）对汾西TFC 6905-3型发电机机体的模态分析可知，需要提高其两端板的钢结构或增加厚度来提高整体结构的固有频率.通过模态试验的结果与有限元仿真的结果进行比较分析，显示模态实验结果与自由状态下计算仿真结果相一致，说明自由状态下分析结果更具有准确性.

另外，根据分析可知，由于边界条件的约束不同，约束状态下和自由状态下的固有频率有所差异，机体的固有频率不仅和结构的材料属性（如质量、刚度、阻尼）有关，而且还与边界条件的约束有关.

［1］THORBY D.Structural dynamics and vibration in practice［M］.Hungary：Butterworth-Heinemann，2008：159-180.

［2］HE JM，FU Z F.Modal analysis［M］.Oxford：Butterworth-Heinemann Elsevier Ltd.，2001：79-158.

［3］BALACHANDRAN B，MAGRAB E B.Vibrations［M］.Second Edition.Toronto：Cengage Learning，2009：663-683.

［4］张力，林建龙，项辉宇.模态分析与实验［M］.北京：清华大学出版社，2011：106-130.

（编辑桂金星）