核电站稳压器水位控制系统及其仿真

薛 阳，林 静，李 媛，冯建彪

(上海电力学院自动化工程学院，上海 200090)

稳压器(Pressurizer，PZR)是压水堆核电站的重要设备之一，其控制系统的主要功能是使稳压器内的压力和水位按预期的规律变化.PZR是一个非线性、时变、多干扰、大惯性的复杂系统，内部有加热器、喷淋阀和流量调节阀等复杂的热工和流体力学过程，想要获得精确的数学模型非常困难.由于比例积分微分(Proportion Integral Derivative，PID)控制器不依赖于对象的精确模型，且具有控制原理简单、实现容易、实用性强等优点，目前核电站中稳压器控制系统多采用传统的PID控制，但因其理论本身存在局限性，致使超调量较大，动态性能不佳，控制效果不够理想，因此往往不能满足高性能的要求.基于现代控制理论的多种方法应用于稳压器压力水位控制中，虽然可以获得较好的控制效果，但需要对象的精确模型，且算法复杂.而智能控制理论对被控对象的精确模型没有要求，但也存在很多问题，如应用单纯模糊控制时，系统响应速度加快，动态过程波动剧烈且稳态偏差较大等.自抗扰控制(Active Disturbances Rejection Controller，ADRC)是韩京清研究员在非线性PID基础上提出的一种适应数字控制需要的控制策略.与经典PID控制理论相比，其省去了积分环节，增加了扩张状态观测器以实现对系统内部模型摄动和外部扰动的实时估计，并采用非线性误差状态反馈策略，保留了PID控制器的优点，克服了PID控制精度低的缺陷.

本文将自抗扰控制技术引入稳压器水位控制系统中，对PZR水位进行控制，最后在Matlab软件平台上进行仿真分析.

1 稳压器水位控制系统

压水堆核电站中的稳压器是对一回路压力进行控制和超压保护的重要设备，其位置见图1.［1］稳压器是一个立式圆筒，上部是蒸汽，下部是水，其主要由电加热器组、喷淋系统、安全阀组和相关仪表等组成.稳压器控制系统是核电站主要的过程控制系统之一，可分为保持稳定一回路的压力、防止沸腾的稳压器压力控制系统和保持一回路的水装量的稳压器水位控制系统.两者共同构成重要的反应堆控制系统，但同时相互独立.通常利用控制电机调节比例阀的方法来实现水位的控制，但这种方法中PI控制器使系统的超调量较大，系统的安全系数较低.

图1 压水堆核电站工艺流程

稳压器水位控制系统的工作过程是，由于反应堆的功率变化导致一回路水温发生变化，从而使得稳压器的水容积发生变化.为了保证在此功率下的实际水位值和整定值相一致，化学与容积控制(RCV)系统中的阀门会根据实际功率的变大或变小随之变化，若实际功率变大，水位升高，则阀门将关小，上充流量减少，反之则增多.其目的是保持稳压器的实际水位能和此功率下的整定值相符.

稳压器水位控制的基本原理是保持下泄流量不变，通过改变上充流量来调节稳压器水位.图2为稳压器水位控制原理图.

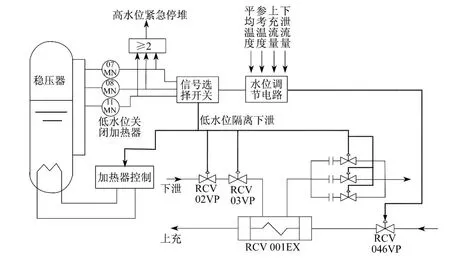
图2 稳压器水位控制原理

图3为水位调节电路原理图.由007MN，008MN，009MN测得3个水位实测信号，输入信号选择开关，经过筛选后其中的一个水位实测信号被送往水位调节电路.在水位调节电路中，由一回路平均温度Tav按指定曲线产生水位整定值，同时引入一回路平均温度的参考值Tref对其进行修正，然后与水位测量信号比较得到水位偏差值.由于上充流量与下泄流量的不平衡会对水位产生影响，所以也要将其实测值引入计算.调节电路经过计算，将开度调节信号输送给上充流量调节阀，从而使上充流量发生变化，起到调节稳压器水位的作用.

图3 水位调节电路原理

2 自抗扰控制器基本结构解析

自抗扰控制技术的核心是将系统的未建模动态和未知外扰作用归结为对系统的总扰动，并利用非线性状态观测器对总扰动进行实时估计，在控制信号中给予补偿.ADRC具有算法简单、超调量小、系统响应快、抗干扰能力强，以及实用性强、适应范围广等特点.现已应用于电力、航空航天、化工和军工等多种领域.

跟踪微分器(Tracking Differentiator，TD)、扩张状态观测器(Extended State Observer，ESO)和非线性状态误差反馈控制律(Nonlinear State Error Feedback Law，NLSEF)是自抗扰控制器的3个核心部分.其中TD为系统输入安排过渡过程，得到光滑的输入信号(即跟踪信号)并提取跟踪信号的微分信号，解决了PID中快速性和超调之间的矛盾.ESO是ADRC中最核心的部分，将控制对象的未知部分和未知扰动作为系统的总扰动进行实时估计，以前馈的形式给予补偿，其作用相当于反馈线性化方法，将非线性系统转化为积分器串联型结构形式.NLSEF的功能是将TD给出的跟踪信号及其微分信号和ESO得到的对象模型的状态估计通过非线性函数进行组合，其结果作为被控对象的控制量，以增强系统的鲁棒性.［2］

本文以二阶控制对象为例(一般高阶控制对象可近似简化为二阶控制对象［3］)，其微分方程为:

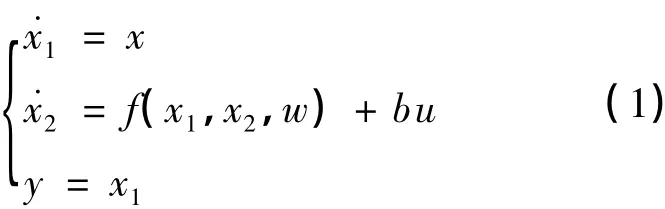
式中:u，y——被控对象的输入信号和输出信号;

x1——y的状态估计信号;

f(x1，x2，w)——包含了系统的所有未建模动态特性.

图4为典型二阶自抗扰控制器的结构图，虚框部分为自抗扰控制器.

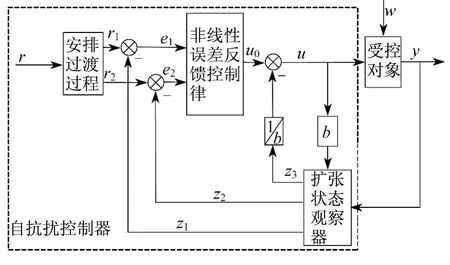
图4 典型二阶自抗扰控制器的结构

2.1 跟踪微分器

跟踪微分器(TD)是一个非线性环节:向TD输入一个信号v(t)，得到该信号的跟踪信号v1(t)及其微分信号v2(t)，其中v1(t)跟踪v(t)，v2(t)=˙v1(t).

二阶跟踪微分器的离散动态方程为:

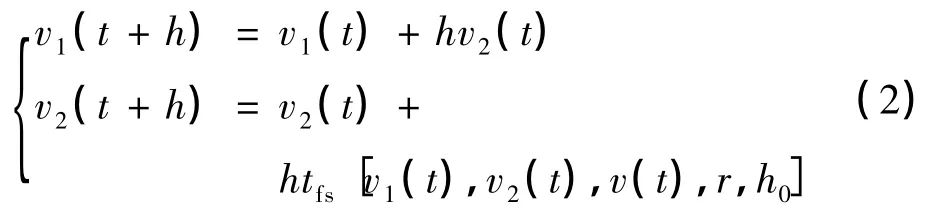
式中:h——采样步长;

h0——滤波因子;

r——速度因子.

tfs(v1(t)，v2(t)，r，h0)为时间最优控制综合非线性函数，其表达式为:

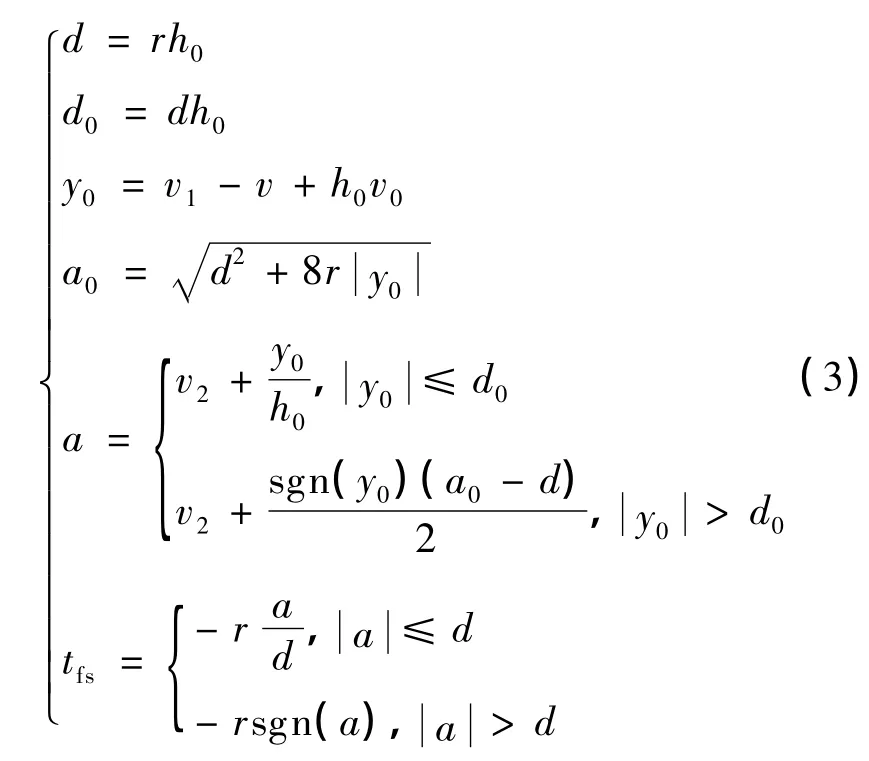
式中的 d，d0，y0，a0，a 均为中间变量.

2.2 扩张状态观测器

二阶自抗扰控制器中的状态观测器是三阶的，其离散动态方程为:

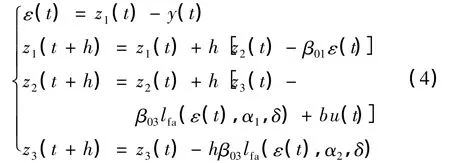
式中:u(t)，y(t)——对象的输入和输出，均是ESO的输入量;

z1，z2——对象状态变量的估计;

z3——对象的内扰和外扰实时总和作用的估计;

b0——对b的估计值;

ε，α——非线性函数 lfa(ε，α，δ)的假设变

δ——可调参数;

β01，β02，β03——增益，为 ESO 的可调参数.

这一扩张状态观测器是独立于对象模型和外扰作用的，其动态特性主要取决于增益 β01，β02，β03，并且响应越快，估计的精度越高.当外扰频率较高时，ESO需要减小h来提高跟踪精度.

2.3 非线性状态误差反馈控制律

TD给出的跟踪信号v1(t)及其微分信号v2(t)与ESO给出的状态估计z1和z2形成两个误差，即:

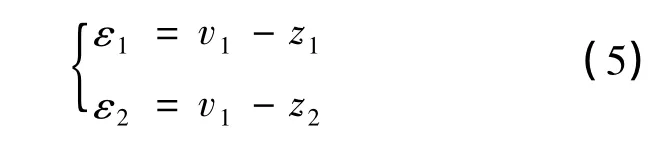
然后用ε1和ε2的适当非线性函数产生u0，其表达式即为非线性状态误差反馈控制律，可以取为:

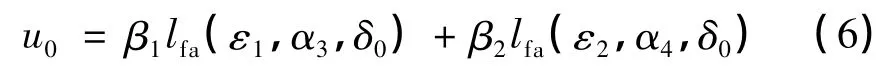
式中:β1，β2——NLSEF 的可调参数.

由式(6)可知，反馈控制律中只存在比例和微分环节，省去了积分环节.

2.4 扰动估计及动态反馈线性化

对于式(1)所表示的二阶对象，将被控对象的控制量u分解为两个量，即:

式(9)即为线性标准积分器串联型对象的表达式.因此，ESO和式(1)将对象的内扰和外扰的总和作用给予了全部补偿，实现了闭环系统的动态反馈线性化，从而使自抗扰控制器具有抗扰能力.

3 仿真研究

文献［4］中通过核电站稳压器水位特性实验，得到了其数学模型为:

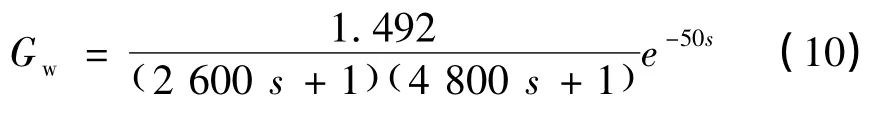
由式(2)至式(9)可知，ADRC中TD的参数有 h，h0，r;ESO 的参数有 δ，α1，α2，β01，β02，β03;HLSEF 的参数有 α3，α4，β1，β2，δ0，b.其中一部分参数是根据经验设定的，如 β01，β02，β03是根据采样步长 h 决定的，只要 h 相同，则 β01，β02，β03相同;r是由所要求的过渡过程的快慢和被控对象的承受能力共同决定的.自抗扰控制器各部分参数的整定直接关系到其控制性能的好坏，尤其是ESO参数的选取.在整定参数时，ADRC的3个部分(TD，ESO，NLSEF)相互独立，先分别整定TD和ESO的参数并达到较理想的效果，再整定NLSEF参数，从而对整体参数进行调整.［5］

(1)TD参数整定 TD有h，h0，r 3个参数需要整定.首先确定采样步长h和速度因子r，当TD输出的跟踪信号对输入信号的跟踪精度在要求范围内，则此时的h和r为整定值.另外，考虑到r越大过渡过程越快，再适当修正参数r，但是r不能过大，否则会影响TD输出信号的品质;同时相应地调节h0，以保证TD有较快的响应速度.

(2)ESO参数整定 ESO是ADRC的核心部分，其跟踪精度的高低直接影响整个ADRC的控制效果.β01，β02，β03可以按 β01=1，β02=1/(3h0.5)，β03=2/(82h1.5)进行数量级的选择，然后根据得到的仿真曲线进行修正.ESO的参数多，选取复杂，需要反复整定才能达到理想效果.

(3)NLSEF参数整定 NLSEF参数的选取会影响系统的性能指标.β1是比例增益，β2为微分增益，其整定方法与PID控制中的比例和微分环节相同.

下面通过仿真结果研究ADRC的阶跃响应及其抗干扰的特性，并将仿真结果与PID控制器进行比较.在PID和ADRC分别控制下稳压器压力控制的阶跃响应曲线如图5所示.

图5 PID和ADRC控制下稳压器水位系统响应曲线

此外，为了验证ADRC的抗干扰能力，在系统达到稳定运行后，在2 400 s时加入方波扰动，其中扰动持续时间为100 s，扰动幅值为0.04.仿真时间设定为3 000 s，PID控制器和自抗扰控制器各参数分别设定如下:h=0.01，h0=0.01，r=0.01;δ=0.5，α1=0.5，α2=0.35，β01=235，β02=300，β03=2 600;b=5，δ0=0.5，α3=0.5，α4=0.25，β1=0.26，β2=0.7.

根据PID参数的工程整定方法，其各参数分别设定为 Kp=700，Ki=2.25，Kd=0.5.

图5表明，与PID控制相比，ADRC控制下的超调量较小，调节时间较短，稳态误差较小，且在加入方波扰动后的波动较小，更容易回到设定值，这说明其抗干扰能力较强.但从图5也可以看出，ADRC的调节仍存在不足之处(如响应速度慢)，因此还需要进一步改进.

4 结语

自抗扰控制算法原理易于理解，不依赖于被控对象模型，具有很高的工程实用价值.本文将自抗扰控制技术应用于稳压器水位控制系统中，解决了强干扰、大时滞的问题，并与PID控制器仿真曲线进行了对比.仿真结果表明，自抗扰控制技术在超调量性能上明显优于传统PID控制，且具有较强的抗干扰性.但自抗扰控制器在响应速度和上升时间方面的控制效果并不理想，仍需作进一步的研究和改进.

［1］马进，刘长良，李淑娜.稳压器压力水位控制系统建模与仿真［J］.核科学与工程，2010，30(1):9-14.

［2］姜萍，郝靖宇，宗晓萍，等.自抗扰控制器的SIMULINK建模与仿真［J］.自动化技术与应用，2010，29(2):1-4.

［3］程启明，汪明媚，薛阳，等.核电站蒸汽发生器水位控制系统的仿真研究［J］.计算机仿真，2012，29(2):188-193.

［4］张国铎，杨旭红，卢栋青，等.核反应堆稳压器水位和压力控制系统研究［J］.化工自动化及仪表，2013，40(1):35-38.

［5］朱丽玲，于希宁，赵凯君.基于自抗扰技术的主气温控制系统［J］.计算机仿真，2006(8):211-214.