多模型预测控制及其在火电厂过热汽温控制中的应用

牛玉广，李晓明，赵子昂

(华北电力大学a.新能源电力系统国家重点实验室，b.控制与计算机工程学院，北京 102206)

随着以煤炭和石油为代表的传统能源成本的上升，电力企业对火电机组的经济、节能运行提出了更高的要求.过热蒸汽温度(简称过热汽温)是火电机组的重要被控参数之一，稳定的过热汽温对于提高汽轮机效率，减少锅炉和汽轮机的热应力，提高电网消纳新能源电力的能力具有十分重要的意义.目前火电机组普遍采用常规PID控制器，它是根据某一工况下的近似线性模型进行整定的.由于火电机组被控过程普遍具有大惯性、大滞后和时变的特点，常规PID控制方法往往不能取得令人满意的控制效果.［1］预测控制产生于20世纪70年代，预测控制对有大惯性、大滞后、时变特性的工业对象具有较好的控制品质和较强的鲁棒性，因而受到人们的重视，广泛应用于生产实践并取得了大量的成果.［2-3］

基于线性模型的模型预测控制(Model Predictive Control，MPC)在热工控制系统中应用较为广泛，但是用线性动态模型描述大范围变化的强非线性过程是不充分的.［4］而实际过程大多为非线性的，这一建模方式的局限性以及对控制品质越来越高的要求，共同促进了非线性MPC的发展.

人工神经网络(Artificial Neural Network，ANN)具有表达任意非线性映射的能力，被广泛应用于非线性建模和控制.STAIB W E等人将人工神经网络技术应用于电弧炉(多变量、非线性、时变特性，难以用传统数学模型描述的系统)的建模和控制，取得了较好的效果.［5-6］BONGARDS M等人将模糊控制与ANN建模结合起来，在污水处理方面取得了良好的效果.［7］柴天佑将ANN与自适应控制相结合，实现了多变量系统的解耦控制，并将该方法应用于火电机组钢球磨煤机控制中，极大地提高了磨煤机的制粉效率.［8］陈立甲等人利用锅炉过热器系统机理和ANN复合建模方法建立了锅炉过热器系统的复合模型，仿真表明该模型具有较高的精度.［9］

基于ANN技术的MPC，首先要利用学习算法对所选定的ANN模型进行训练.为了确保ANN建模达到预期的精度，其训练数据应该覆盖被控对象的全局工作区间.如果被控对象的全局工作区间波动较大，则很难训练全局ANN模型.［10］为了解决这一问题，本文在多模型预测控制方法［11］的基础上，提出了一种新的控制方法，即在若干工作点构建局部ANN模型，通过局部模型加权输出的方式得到被控对象的ANN模型预测输出.因此，本方法只需一个控制器即可实现对被控对象的全工况控制.通过对某600 MW直流锅炉过热汽温控制系统的仿真结果表明，与常规PID控制相比，本文所提出的控制方法具有较好的变负荷适应性，在负荷大范围变化时取得了较好的控制效果和较强的鲁棒性.

1 改进Elman神经网络建模

本文采用改进Elman神经网络作为预测模型，其结构由输入层、隐层、承接层、输出层4部分组成.其中，输入层为信号传输层，仅起信号传输的作用;输出层起信号线性加权的作用;隐层激发函数可为线性或非线性函数，多数情况为Sigmoid非线性函数;承接层的作用是储存隐层相对应单元的前一时刻的输出值，可视为具有一步迟延功能的延时算子，因此承接层又叫做内部反馈层.隐层和承接层具有相同的单元数，输入层、隐层、输出层的连接方式与前馈ANN网络相类似.

Elman回归ANN网络的特点是:隐层单元的输出通过承接层的延迟、记忆，最后反馈到该隐层单元的输入，这种自我连接方式使得Elman网络对历史数据具有独特的敏感性.Elman网络独特的结构——内部反馈层，提高了神经网络处理动态信息的能力，有利于对动态过程进行建模.

当Elman神经网络用于辨识单输入单输出过程时，其输入层只需要2个输入单元，输出层仅需要1个输出单元.与输入输出数据经多分头时延系统连入ANN输入层的静态ANN相比，Elman神经网络的结构较为简单.此外，Elman网络的动态信息仅由内部反馈层提供，不需要将过程状态变量经多分头时延系统作为输入或训练信号.但当Elman网络采用BP算法进行训练时，由于该算法只有一阶梯度，若增加所辨识系统的阶次或该神经网络所含的隐层节点，那么在确保学习收敛的前提下，将导致学习率极小，逼近精度往往不能满足要求，因此Elman神经网络只能辨识一阶线性系统.［12］

为了提高Elman人工神经网络有效辨识高阶系统的能力，需要采用较复杂的学习算法，如动态反向传播学习算法，或者对网络结构进行改造.目前，较为常用的方法是在基本Elman神经网络的承接层增加一个自反馈连接，设定该反馈连接的固定增益为α.这样，承接层单元在k-1时刻输出值的α倍与相对应的隐层单元在k-1时刻的输出之和，即为该承接层单元在k时刻的输出.改进的Elman人工神经网络能有效辨识高阶系统，其结构如图1所示.

令列向量Y(k)为改进Elman网络在k时刻的输出向量，U(k)为k时刻的输入向量，NI为输入节点数，NH为隐节点数，NO为输出节点数，则Y(k)=［y1(k)，y2(k)，y3(k)，…，yNO］T，U(k)=［u1(k)，u2(k)，u3(k)，…，uNI(k)］T.令 XH，XC分别表示隐层单元输入和承接层单元输入;，分别表示第 j个隐层单元到输入层第 i个单元，到承接层第l个单元，到输出层第n个单元的连接权值;θHj，θOn分别表示隐层第j个节点和输出层第k个单元的阈值.

图1 改进Elman神经网络结构

假设输出层激发函数为f2(·)，隐层的激发函数为f1(·)，则Elman神经网络输出层第n个输出值nym(k)为:

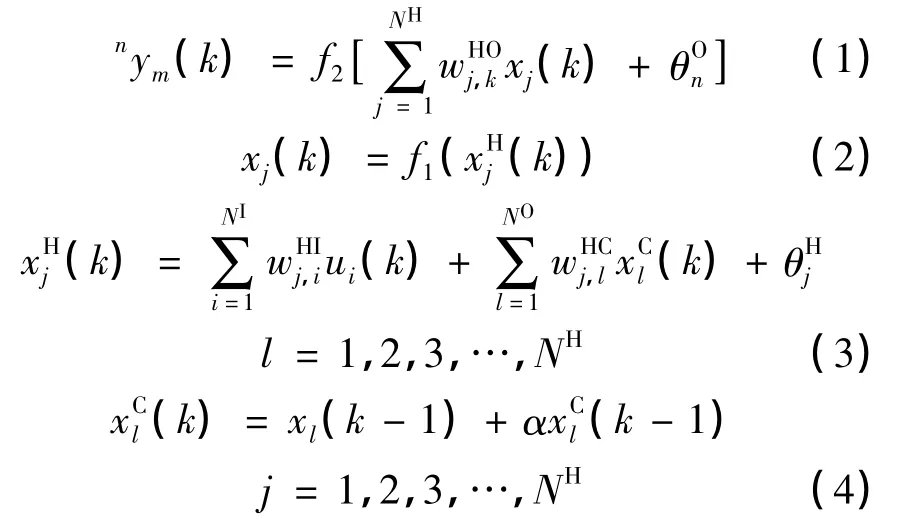
为了进一步提高该神经网络辨识高阶非线性系统的能力，本文采用强跟踪滤波器来训练Elman神经网络.强跟踪滤波器的基本原理是:利用正交原理，强制残差正交或近似正交;引进时变渐进因子，调整时变增益.强跟踪滤波器克服了常规Kalman滤波器的一些缺点，如对初值敏感、鲁棒性差、机动目标跟踪性能差等，具有收敛快、精度高的特点，具体算法见参考文献［13］.

2 多模型预测控制器设计

文献［14］指出直流锅炉过热汽温被控对象的动态模型可由主蒸汽流量、主蒸汽压力以及温度组成的函数表示.其中，对过热汽温的动态特性影响最大的是主蒸汽流量，其次是主蒸汽压力，而温度对其影响程度最小.当直流锅炉运行在稳定工况时，温度的变化波动很小，在控制系统设计过程中可以忽略.此外，在直流锅炉启动、停止或者增加、减少负荷时，主蒸汽流量与主蒸汽压力相互耦合，并且具有相同的变化趋势，即主蒸汽流量减小则压力下降，主蒸汽流量增大则压力上升.相对于蒸汽焓温度通道来说，该变化过程是很快的，因此主蒸汽压力可以近似看作是主蒸汽流量的函数.综上所述，根据主蒸汽流量的不同值便可以确定工作点，并在该工作点下建立过热汽温模型.

2.1 多模型神经网络预测输出

设局部神经网络模型数为N个，y(k)为当前时刻过程值.定义输出残差为(k)=y(k)-(k)，其中第i个局部模型输出值iym(k)可根据式(1)更新.根据贝叶斯概率理论，该局部模型当前时刻的概率值为:［15］

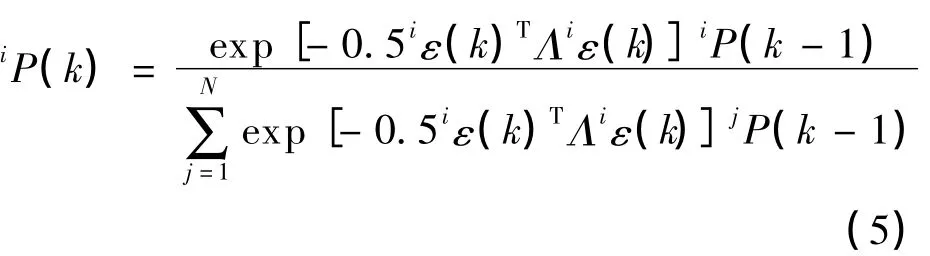
式中:Λ——残差扩展矩阵，可根据需要设定.

由式(5)可知，模型的概率值计算是通过递归的方式进行的.为了防止在递归计算中出现接近于零的数，使参与计算的模型保持一定的活性，人为地设置了一个概率阈值，只有当模型概率值大于该阈值时，该模型才可参与计算.由上述可知，当前时刻的局部模型的权重为:

式中:μ——权重计算阈值.

由式(1)可得出未来k时刻的第i个局部模型预测值为:

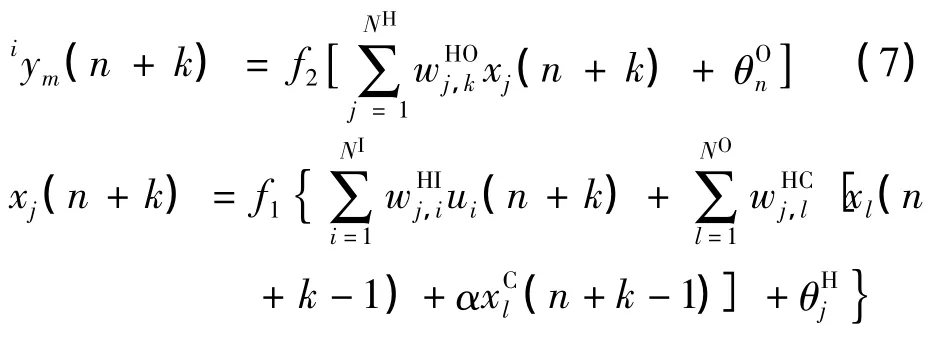
根据式(6)和式(7)可知，神经网络加权预测k时刻的输出为:

2.2 滚动优化

建立如下性能指标函数:

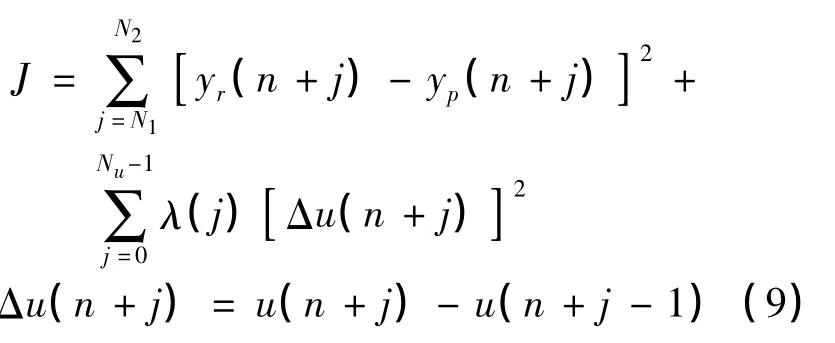
式中:N1——最小预测时域;

N2——最大预测时域;

Nu——控制时域;

yr——参考轨迹;

yp——经反馈校正后的预测输出值;

λ(·)——控制加权值.

性能指标函数最小化算法的目的是确定控制序列 U=［u(n)，u(n+1)，…，u(n+Nu)］T，使式(9)中的性能指标J最小.其中，U可由Newton-Raphson 迭代法得到.［16］

2.3 反馈校正

在实际情况下，由于噪声、模型精度等问题，预测模型输出值与过程输出值之间往往存在误差.为此，需要计算该差值，并利用这一实时信息对MPC算法进行反馈校正，然后再进行滚动优化.误差预测采用误差外推器，表示如下:

式中:Mc——误差外推器阶次;

N1，N2——最小、最大预测步长.

校正后的模型预测输出值为:

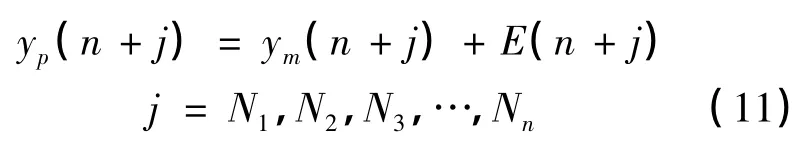
3 仿真及分析

文献［14］给出了某600 MW 直流炉过热气温在100%，75%，50%负荷下的动态模型，如表1所示。基于这3个工况点的多模型神经网络预测控制的结构图如图2所示.图2中局部神经网络模型数N=3，预测模型采用基于强跟踪学习算法的改进Elman神经网络.

表1 过热气温动态模型

图2 多模型神经网络预测控制结构

现假定过热器在某一段时间内处于某一工况(工况4，区别于上述3个局部神经网络模型的标称工作点)下，其气温对喷水扰动的动态特性为:导前区为-2.362/(1+23 s)2;惰性区为1.161/(1+34.6 s)7.

本文采用在设定值端加入单位阶跃扰动的方式验证控制器的鲁棒性和控制效果，同时将多模型MPC方法与常规PID控制［17］进行比较，结果如图3所示.图3a为传统 PID控制下，50%，75%，100%负荷与工况4时的系统响应曲线，其中传统PID控制器在100%工况下整定的.由于传统PID控制是根据某一工况下的近似线性模型整定的，因此当被控对象偏离其整定工况较远时，难以取得满意的控制效果.图3b为采用本文多模型MPC控制策略下的系统响应.由图3a可以看出，随着距离整定工况(100%负荷)越来越远，常规PID控制下的过热气温出现了较大幅度的超调和振荡，在距离最远的50%负荷工况下，出现了严重的发散振荡.由图3b可以看出，采用本文提出的基于人工神经网络技术的多模型MPC控制策略的过热汽温控制系统，在3个建模工况点和工况4均取得了较好的控制效果.

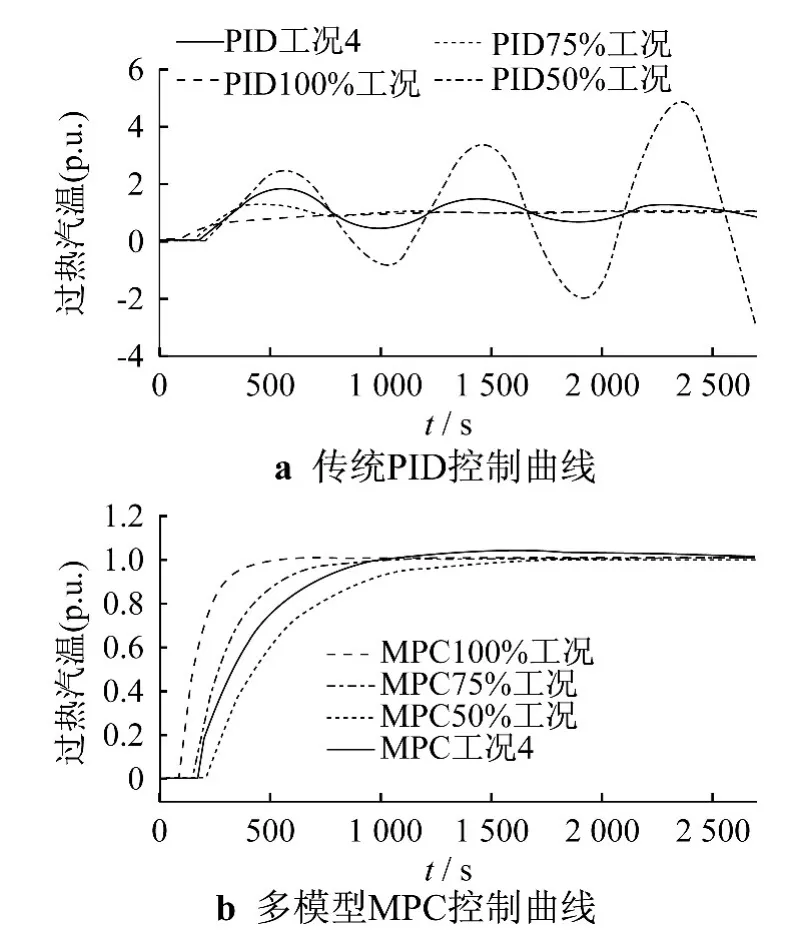
图3 4种工况下传统PID与多模型MPC控制曲线

图4为多模型MPC控制器在工况4下的模型权值曲线.

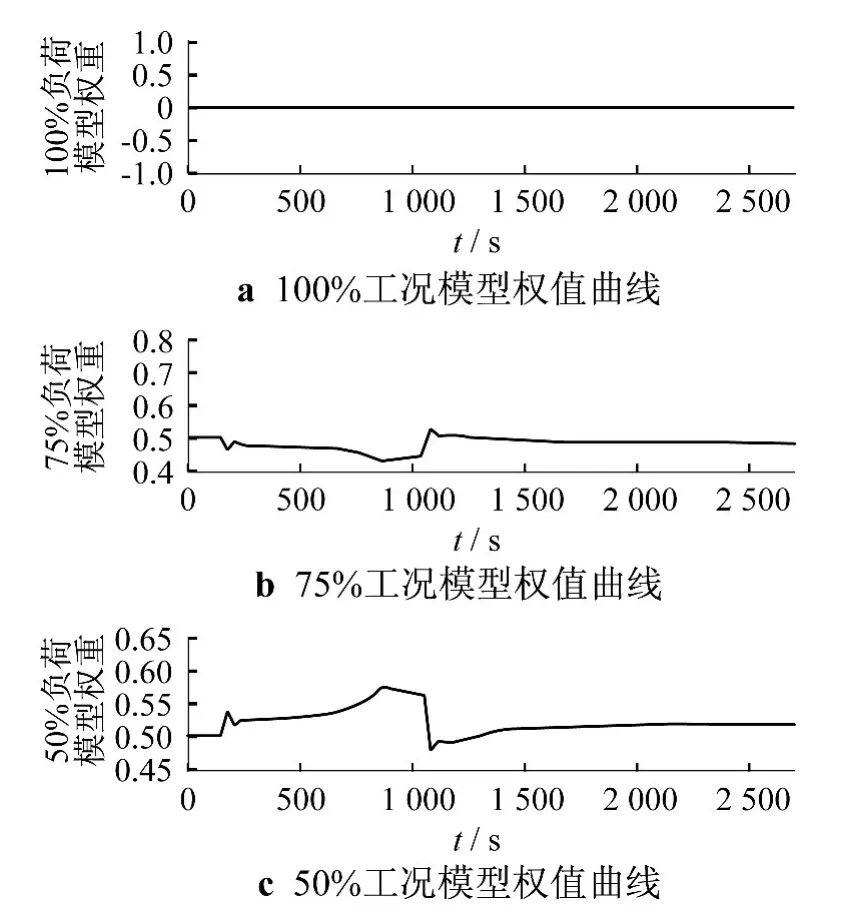
图4 多模型控制器权重变化曲线

由图4可以看出，由于设置了切换阈值，距离工况4较远的100%负荷下的模型并未参与控制.同时，这也从另一方面验证了工况4介于50% ～75%负荷模型之间.仿真表明，在大范围变负荷情况下，多模型MPC控制可实现对过热汽温的稳定控制，具有较好的控制效果和较强的鲁棒性.在仿真过程中，过热汽温控制曲线平滑，模型切换平滑.

4 结论

(1)将贝叶斯估计与神经网络模型相结合，提出了神经网络多模型拟合建模方法，并给出了基于改进Elman神经网络的多模型拟合公式;

(2)利用预测误差的反馈补偿模型预测模型的失配，神经网络模型不需要在线学习，只需进行充分的离线训练;

(3)由于采用了被控对象多模型拟合建模，利用多个局部神经网络模型拟合被控对象模型并预测输出，因此本方法仅用一个控制器即可实现被控对象的全工况控制.

［1］吕剑虹，陈来九.预测控制在热工控制中的应用前景［J］.动力工程，1997，17(2):12-15.

［2］CAMACHO E.F，BORDONS C.Model predictive control in the process industry［M］.New York:Springer，1995:11-20.

［3］MORARI M，LEE J H.Model predictive control:past，present and future ［J］.Comput.Chem.Eng.，1999，23(4-5):667-682.

［9］陈立甲，伞冶，王子才，等.锅炉过热器系统机理与神经网络组合建模方法［J］.中国电机工程学报，2001，21(1):73-76.

［10］HUNT K J，SBARBARO D，Z˙BIKOWSKI R，et al.Neural networks for control systems——a survey［J］.Automatica，1992，28(6):1 083-1 112.

［4］HENSON M A.Nonlinear model predictive control:current status and future directions［J］.Computers and Chemical Engineering，1998，23(2):187-202.

［5］STAIB W E，STAIB R B.Theintelligentarcfurnace controller:a neural network electrode position optimization system for the electric arc furnace［C］∥Neural Networks，International Joint Conference on IEEE，1992:1-9.

［6］STAIB W E，MCNAMES J N.Operating experience from intelligent arc furnace installations［J］.Iron and Steel Engineer(USA)，1994，71(5):38-40.

［7］BONGARDS M.Improving the efficiency of a wastewater treatment plant by fuzzy control and neural networks［J］.Water Science ＆ Technology，2001，43(11):189-196.

［8］柴天佑.多变量自适应解耦控制及应用［M］.北京:科学出版社，2001:178-181.

［11］MAYBECK P S，STEVENS R D.Reconfigurableflight control via multiple model adaptive control methods［J］.Aerospace and Electronic Systems，IEEE Transactions on，1991，27(3):470-480.

［12］周洪煜，张坚，常力民.基于 E1man网络的过热汽温隐式广义预测控制［J］.自动化技术与应用，2003，22(3):13-16.

［13］赵奇，刘开第，庞彦军.Elman神经网络训练方法及其在非线性系统辨识中的应用［J］.煤矿机械，2005，5(5):73-74.

［14］杨锡运，徐大平，柳亦兵，等.过热汽温多模型预测函数控制策略的研究［J］.动力工程，2005，25(4):537-540.

［15］KUURE-KINSEY M，Bequette B W.Multiple model predictive control:a state estimation based approach［C］∥American Control Conference，ACC07 IEEE，2007:3 739-3 744.

［16］SOLOAWY D，HALEY P J.Neural generalized predictive control［C］∥Proceeding of the 1996 IEEE International Symposium on Intelligent Control，Dearborn，M.I.，USA，1996:277-282.

［17］诸静.智能预测控制及其应用［M］.浙江:浙江大学出版社，2000:15-18.