基于人工神经网络的风电功率预测优化算法

朱海婷，杨宁，王博

（上海电力学院a.电气工程学院，b.自动化工程学院，上海 200090）

风电作为一种可再生能源，以其不消耗能源、无空气污染、建设成本和可持续成本较低等优点成为发电领域的新选择.但持续变化的风速和环境因素导致了风电厂的输出功率波动较大.为了提升风电能源的经济效益和电网容纳程度，对风速和风电功率进行精确预测是至关重要的.

目前，国内用于风电功率预测的算法有很多，［1-2］主要包括智能类方法和时序类方法.智能类方法是用人工智能方法建立输入变量与输出变量之间的特定关系，如BP神经网络、［3］RBF神经网络、［4］Elman神经网络、［5］遗传算法（GA）、［6］粒子群算法（PSO）、支持向量机回归法（SVM）、［7］灰色模型、［8］模糊逻辑等.时序类方法是寻找风电功率历史数据在时间上的相关性，如持续预测法、［9］指数平滑法、［10］卡尔曼滤波法［11］等.

殖民竞争算法（Imperialist Competitive Algorithm，ICA）［12］是ATASHPHAZ-Gargari和LUCAS于2007年提出的，它是一种模拟人类社会殖民竞争过程的新颖的元启发式算法.国内对这种方法的研究不多，主要用于离散制造系统优化［13］和切削参数优化［14］等问题.本文在国外学者研究［15］的基础上提出了一种结合人工神经网络和殖民竞争算法的风电功率预测方法.这种新型算法运用殖民竞争算法优化BP人工神经网络的初始权值和阈值，采用实际风电厂的数据对该方法进行分析和验证，结果表明，该方法能有效提高风电功率预测的准确性.

1 风电功率预测模型

本文所有数据均来源于江苏省某风电厂的SCADA系统和测风塔.

1.1 算法流程

ICA算法是一种新智能算法，“国家”为群体中的个体，每个国家分别代表待优化问题的一个解.在初始群体中，依据国家强弱程度的不同将其分为“殖民国”和“殖民地”，一个帝国是一个殖民国与其占领的殖民地的总称.经过帝国间的竞争，当群体只剩下最后一个帝国时算法结束.算法的流程图如图1所示.

1.2 帝国初始化

在一个Nvar维的最优化问题中，一个国家即为一个1×Nvar的矩阵.该矩阵定义为：

式中：p1，p2，p3，…，pNvar——被优化的变量.

国家中的一个变量可以理解为该国家的特殊属性，也就是算法中需要优化的最小的成本值.每个国家的成本由变量所组成的函数决定，该函数为：

图1 ICA算法流程

首先，初始化国家数量Ncountry，选取其中Nimp个能量最大的的国家形成殖民国.剩下的Ncol个最初国家作为这些殖民国的殖民地，相应的殖民国和殖民地组成一个帝国.

为了形成最初的帝国，依据各殖民国的能量情况来确定殖民地，每个殖民国的成本被定义为：

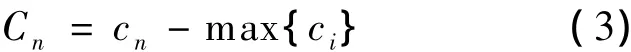
式中：cn——第n个殖民国的成本值;

Cn——第n个殖民国归一化之后的成本值.

每个归一化之后的能量pn由Cn决定，即为：

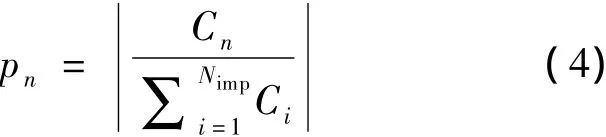
最初的殖民地的分配依赖于其所属的殖民国的能量，因此最初殖民地的分配为：

式中：NCn——第n个帝国拥有的殖民地数量.

能量较大的殖民国拥有较多的殖民地数量，而能量较小的殖民国则拥有较少的殖民地.

1.3 帝国的同化和更新

殖民国试图去吸收和同化自己的殖民地，以使其帝国更加壮大，这个过程可以表示为殖民地沿着坐标轴向着殖民国随机移动，如图2所示.

图2中，x为一个随机数，服从均匀分布x～U （0，β×d），d表示殖民地与殖民国之间的距离，若β＞1，则会使殖民地从两边趋向于殖民国.但帝国内的吸收并不会直接使殖民地向殖民国移动，因此引入了一个随机的角度θ模拟该运动，θ参数服从均匀分布θ～U（－γ，γ），γ为调整偏移量的参数.一般将β设为2，γ设为π/4.

图2 殖民地向其相关殖民国的移动过程示意

帝国内的更新是指在相对短的时间内，殖民地的能量和组织结构所发生的变化.一般将更新率设为0.3，即帝国中有30%的殖民地会随机改变位置.

1.4 帝国竞争

一个帝国的总能量主要是由其殖民国的能量所决定的，但殖民地的能量也会对帝国的能量有所影响.因此，一个帝国的总成本可概括为：

式中：TCn——第n个帝国的总能量;

ζ——一个较小的正数.

若ζ变大，则殖民地对帝国的影响就会变大.根据殖民国的总能量可以确定每个帝国占领其他殖民地的可能性，即：

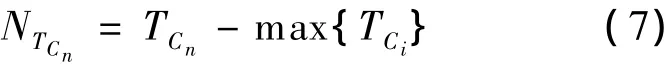
式中：NTCn——第n个帝国归一化之后的能量.

每个帝国占有自由殖民地的可能性为：

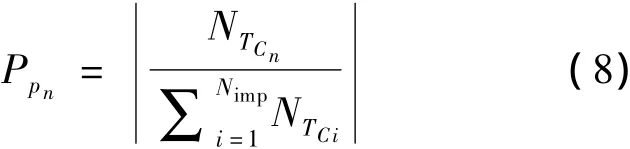
将自由殖民地分配给殖民国的过程，可引入向量P来表示，即：

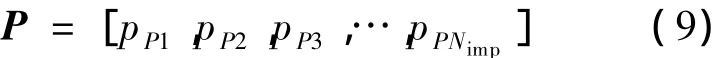
向量R与向量P的形式相同，其元素服从均匀分布：

用向量P减去向量R得到向量D，即：

在向量D中，数值最大的殖民国将会占领上述自由殖民地.

1.5 帝国删除及算法终止

当一个帝国失去所有殖民地时，当前群体将删除该帝国，算法停止.

从以上理论可以看出，殖民竞争算法并非梯度类下降算法，其仿人类社会学的理论机制使得其自身对样本的依赖性不大，即使输入样本有缺失也可以很好地运行.该算法的结构独立性很强，是一种全局优化算法，所有信息均有保留，可以防止陷入局部极值.这种新型算法的优势可以弥补BP算法的不足.

2 ICA优化BP神经网络的权值

BP（Back Propagation）神经网络是一种多层前馈神经网络，也是最基本最简单的神经网络，其特点是信号前向传递和误差反向传播，学习过程由信号的正向传递和误差的反向传播两个过程组成.BP神经网络的结构包含输入层、隐含层、输出层3层，其结构如图3所示.

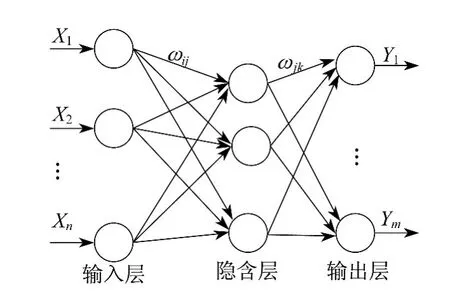
图3 BP神经网络结构

图3中，X为输入信号;Y为输出信号;ωij，ωjk分别为输入层与隐含层、隐含层与输出层之间的连接权值.

在信号的正向传递过程中，输入信号从输入层节点依次传过各隐含节点，然后传到输出节点.误差的反向传播过程中，误差经过输出层，按误差梯度下降的方式对各层权值进行修正，并向隐含层和输入层逐层反传.这两个过程一直持续到网络输出的误差减少至设定的精度范围内，或达到预先设定的迭代次数为止.

从算法上分析，BP算法在解空间内，沿着误差表面的最速下降向量向着全局搜索最优值做梯度下降，这种基于梯度的算法在很大程度上依赖于样本，且容易陷入局部最优值.BP神经网络的初始化权值和阈值一般采用随机的方法，这也造成了该算法的结果不稳定和求解的困难.

为了克服BP算法快速却容易陷入局部极小值的缺点，使用ICA新型全局优化算法.将BP神经网络的连接权值和阈值作为ICA算法的变量，将BP神经网络预测的均方误差eMSE作为ICA中的目标函数.采用ICA算法的目的是使目标函数达到最小值，即使得BP神经网络预测的误差达到最小，此时的ICA算法变量即为最优的网络权值和阈值.使用这组变量作为BP神经网络的网络初始化权值和阈值，并进行功率预测，便可更快更好地得到预测结果.ICA-BP算法的流程见图4.

图4 ICA-BP算法流程

本文所选的ICA-BP网络为3层神经网络，输入层、隐含层、输出层节点数分别为2，3，1.输入为风电厂某风机2013年5月前15天的SCADA系统风速和测风塔风速，输出为对应时间点的功率，时间间隔均为1 h，预测第16天的24 h功率.国家和殖民国数目分别为200和10，迭代次数为10，参数β为2.

3 实验结果及误差分析

3.1 非线性函数求极值

采用Matlab软件对该算法进行仿真实验.为了验证ICA算法编程的正确性，先用其求解一个非线性函数的最小值.函数如下：

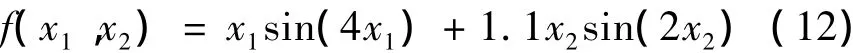
其中x1和x2的取值范围为［－10，10］，几次实验结果均为－18.554 7，即该函数在此区间范围内的最小值为－18.554 7，由此证明了算法编程的可行性.用五角星代表殖民国，圆形代表殖民地，则实验过程如图5所示.

图5 殖民竞争算法实验过程示意

由图5可以看出，在殖民竞争算法过程中代表殖民地的圆形逐渐减少，而代表殖民国的五角星不断变大.

3.2 ICA-BP算法用于风电功率预测

在新算法中，用ICA算法优化BP神经网络，将ICA的目标函数设为均方差eRMSE，即：

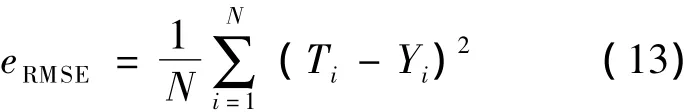
式中：Ti——目标输出;

Yi——训练输出.

通过算法运行，得到优化过后的权值和阈值，从而使eRMSE达到最小，实验结果如图6所示，目标函数结果为0.009 8.

将ICA算法中构成最小目标值函数的变量保存，即为BP神经网络的初始权值和阈值，则ICA-BP神经网络风电功率预测实验结果如图7所示.

图6 ICA算法迭代结果

图7 ICA-BP神经网络风电功率预测结果

遗传算法和粒子群算法也是风电功率预测中常用的人工智能算法，其算法机理与殖民竞争算法类似，但又有很大不同.为了与前文ICA-BP算法的实验结果进行比较分析，在相同条件下对遗传算法优化BP神经网络的功率预测和粒子群算法优化BP神经网络的功率预测进行编程实现，实验结果见表1.其中，将ICA-BP神经网络的误差设为平均绝对百分比误差eMAPE及均方根误差eRMSE.

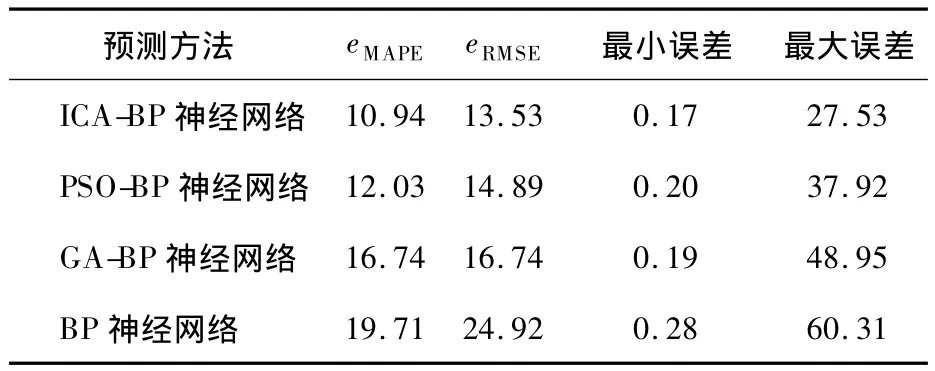
表1 4种方法预测风电功率的结果%

由表1可以看出，BP神经网络由于其初始化权值和阈值为随机选取，造成了实验结果差异性较大，而3种优化BP神经网络方法的实验结果相对波动不大，按照预测效果依次排序为ICA-BP最好，PSO-BP次之，GA-BP较差.其中，ICA-BP神经网络预测的样本点误差大部分都集中在10%以内，预测精度较高，从而证明了本文所提出的基于殖民竞争算法优化BP神经网络方法的有效性.

4 结语

在相同情况下，ICA-BP神经网络方法比其他算法能够更加有效地提高风电功率预测精度.由于篇幅所限，本文的实验数据都进行了简化处理，并没有加入天气等影响功率预测的数据.另外，还应结合混沌理论等方法进一步优化ICA算法，以得到更好的功率预测效果.

［1］崔垚，王恺.短期风电功率预测模型研究综述［J］.电子世界，2012（12）：53-54.

［2］王健，严干贵，宋薇，等.风电功率预测技术综述［J］.东北电力大学学报，2011，31（3）：20-24.

［3］郭琦，鲍金春，宋继光.基于BP神经网络的风电功率预测［J］.电源技术应用，2011，14（6）：14-18.

［4］武小梅，白银明，文福拴.基于RBF神经元网络的风电功率短期预测［J］.电力系统保护与控制，2011，39（15）： 80-83.

［5］张靠社，杨剑.基于Elman神经网络的短期风电功率预测［J］.电网与清洁能源，2012，28（12）：87-91.

［6］王德民.基于遗传算法优化BP神经网络的风电功率预测［J］.电子设计工程，2013，21（22）：95-98.

［7］李洪江，张茂林，张子泳，等.基于自适应PSO_SVR的风速风功率预测［J］.云南电力技术，2013，41（3）：46-49.

［8］李俊芳，张步涵，谢光龙，等.基于灰色模型的风速-风电功率预测研究［J］.电力系统保护与控制，2010，38（19）： 151-159.

［9］连文莉，黄成辰，吕昌霖.采用时间序列预测风电场出力［J］.电网与清洁能源，2011，27（12）：112-117.

［10］卢永芳，程志磊，王晓卫，等.基于时序指数平滑法的风电场功率预测研究［J］.工矿自动化，2012（8）：75-78.

［11］赵攀，戴义平，夏俊荣，等.卡尔曼滤波修正的风电场短期功率预测模型［J］.西安交通大学学报，2011，45（5）： 47-51.

［12］ATASHPAZ-Gargari，LUCAS C.Imperialist competitive algorithm：an algorithm for optim ization inspired by imperialistic competition［C］∥Proceedings of the IEEE Congress on Evolutionary Computation.Singapore：IEEE，2007：4 661-4 667.

［13］连坤雷.殖民竞争算法在离散制造系统优化问题中的应用研究［D］.武汉：华中科技大学，2012.

［14］陈志楚，李聪，张超勇.基于帝国主义竞争算法的切削参数优化［J］.制造业自动化，2012，34（12）：10-15.［15］BIGDELIN，AFSHAR K，GAZAFROUDI A S，et al.A comparative study of optimal hybrid methods forwind power prediction in wind farm of Alberta，Canada［J］.Renewable＆Sustainable Energy Reviews，2013（27）：20-29.

（编辑白林雪）