过热汽温的改进型Smith预估复合模糊控制

孙宇贞

(1.上海电力学院自动化工程学院，上海 200090;2.同济大学电子与信息工程学院，上海 201804)

随着火力发电厂机组容量的增大，机组由过去的亚临界汽包炉机组逐步过渡到超临界和超超临界直流炉机组，其过热汽温被控对象也呈现时变、非线性、大滞后、大惯性等复杂的对象特性，如果单纯采用传统的串级控制方案，则控制较为困难，且控制效果不理想.［1］

本文选取了模糊与PID并联复合控制方案，将模糊控制器的输出与PID控制器的输出共同作用于执行机构，以控制过热汽温.该方法综合了模糊控制和PID控制的优点，控制曲线效果超调小、调节时间短，系统的鲁棒性和适应性有所增强.同时采用改进型的Smith预估算法用以补偿对象的大迟延特性，而且改进型的Smith预估器在模型不准确的情况下也能有较好的适应性.

1 复合模糊PID控制

本控制系统采用的复合模糊PID控制实质上是将模糊控制器与PID控制器并行工作，共同完成控制.模糊控制是将操作者或专家的控制经验和知识表示成语言变量描述的控制规则、然后用这些规则去控制系统的一种智能型控制算法，对复杂的非线性系统的控制有较好的适应性.［2］而传统的PID控制在调整稳态误差，使系统简单易行上具有无可比拟的优势.

其中模糊变量选择二输入一输出的模式，E(温度与设定值之差)和EC(偏差变化速率)作为输入，喷水阀门的开度U作为输出.定义的函数模糊语言变量子集为PB(正大)、PM(正中)、PS(正小)、Z0(零)、NS(负小)、NM(负中)、NB(负大)7个等级，各模糊变量隶属函数均选用三角形.

模糊规则库采用如下语言形式:

(1)If E is NB，and ECis NB，then U is PB;

(2)If E is NM，and ECis NB，then U is PB;

(3)If E is NS，and ECis NB，then U is PB;

(4)If E is ZO，and ECis NB，then U is PM;

(49)If E is PB，and ECis PB，then U is NB.其模糊规则库符合表1所示的模糊规则.

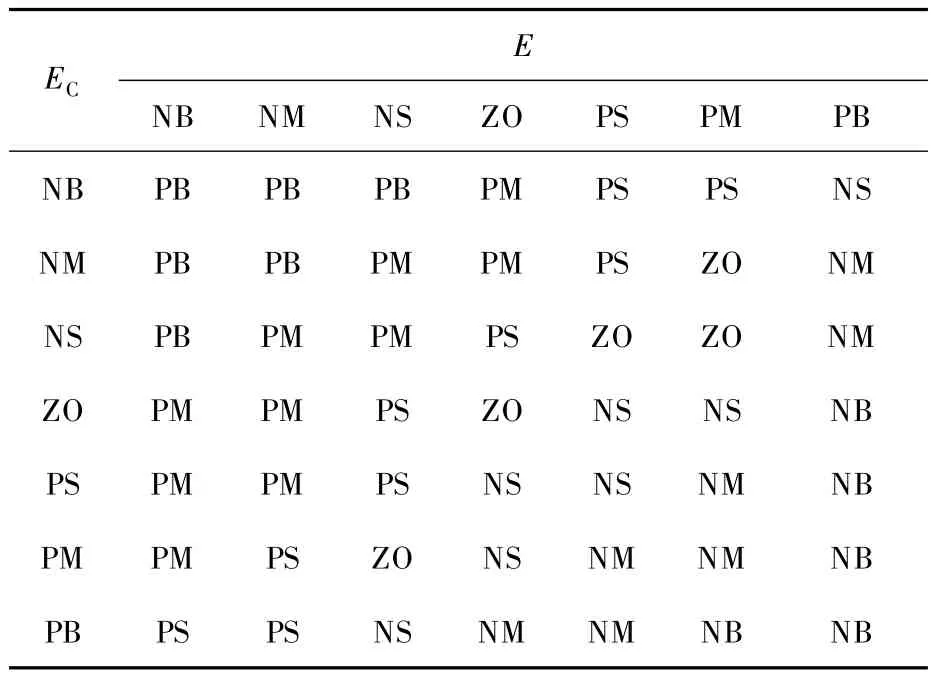
表1 模糊规则

研究表明，这类模糊算法的输入实际上仅包括了偏差和偏差变化率，类似于PD算法，因而难以保证有较高的稳态精度.［3］将容易稳定、并且具有较好稳定特性的PID控制器与上述模糊控制算法相结合，可以提高模糊控制器的控制精度，简化模糊规则，修正模糊因子.

本文所设计的复合模糊PID控制器采用如图1所示的模糊算法与PID控制器并行的方案.其中模糊控制算法的输入采用了过热蒸汽温度与设定值之间偏差E和该偏差的变化率EC，PID控制器的输入采用偏差，通过积分作用保证控制无稳态偏差.模糊算法的输出和PID控制器的输出则通过求和器的相加，共同作为控制量来控制喷水阀开度U.

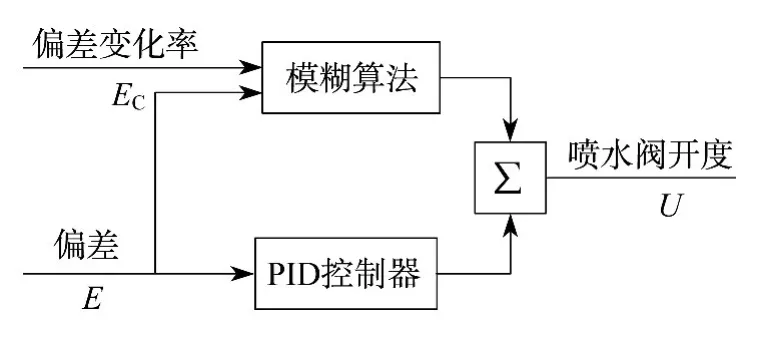
图1 复合模糊PID控制器示意

2 改进型Smith预估器

在具有大滞后的系统中，控制往往会产生较大的超调，稳定时间也会较长，传统的控制技术已经无法满足控制系统的要求，可以采用具有预估补偿作用的Smith预估控制器.比较具有Smith预估器和不具有Smith预估器的复合控制，可以明显地发现，在超调量和稳定时间上，前者优于后者.

传统的Smith预估补偿控制方案的主要原理是预先估出被控过程动态模型，然后将预估器并联在被控过程上，使其对过程中的纯迟延特性进行补偿，力图将被迟延时间τp的被控量提前送入控制器，因而控制器能提前动作，这样就消除了纯迟延特性在闭环中的影响.一般的Smith补偿系统框图如图2所示.

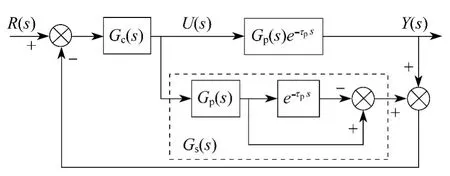
图2 一般的Smith补偿系统

图 2 中，Gp(s)e－τps为广义被控对象的数学模型，其中Gp(s)为不包括纯迟延时间τp的对象模型，GS(s)为Smith预估补偿器.但在实际应用中，Smith预估器需要确知对象的精确数学模型，而且模型有偏差就会产生显著的动态和静态误差，甚至产生振荡.这会影响Smith预估器在实际应用中的控制性能.［4］

改进型Smith预估器见图3.其中 G′p(s)为不包括迟延时间的实际对象模型;Gp(s)为不包括纯迟延时间的预估器模型;e－τ'ps为对象实际滞后环节;e－τps为预估滞后环节.在全补偿情况下，预估器模型与一般Smith预估补偿器所得系统的传递函数式相同.而当预估模型与实际对象模型不一致、存在较大偏差时，可以通过模型输出偏差的比较和修改，减小模型偏差，使系统动态指标均得到改善.［5］

图3 改进型Smith预估方案

3 过热汽温的控制仿真

过热汽温对象具有非线性、大惯性、大迟延的特点，并且受到如蒸汽流量变化、燃烧工况变化、进入过热器的蒸汽温度变化、流过过热器的烟汽温度和流速变化等诸多因素影响，因而其控制算法需要有较好的适应性和动态特性，而传统的控制技术难以取得理想的控制效果.

将改进型Smith预估方案和复合模糊控制器相结合，可以得到如图4所示的控制系统.

图4 改进型Smith预估复合模糊控制方案

该控制方案中，采用改进型Smith预估器以改善对象大迟延特性，采用模糊控制方案以提高系统的适应性，同时通过传统的PID控制器来保证控制算法整定简单易行，并能保证较高的稳态精度.

在文献［6］中，某电厂喷水减温调节方式下过热汽温的动态特性为:

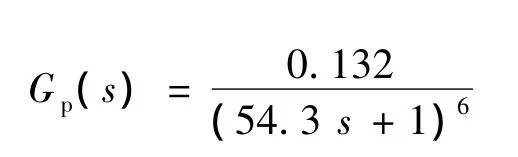
本文改进型Smith预估复合模糊控制的Smith预估器模型的时间常数设为迟延时间τ=180 s，线性部分仅为一阶惯性环节时间常数T=150 s.在与被控对象有一定偏差的情况下，设定值扰动为5℃时，仿真模拟了复合模糊控制与传统的PID控制的响应情况，仿真结果如图5所示.

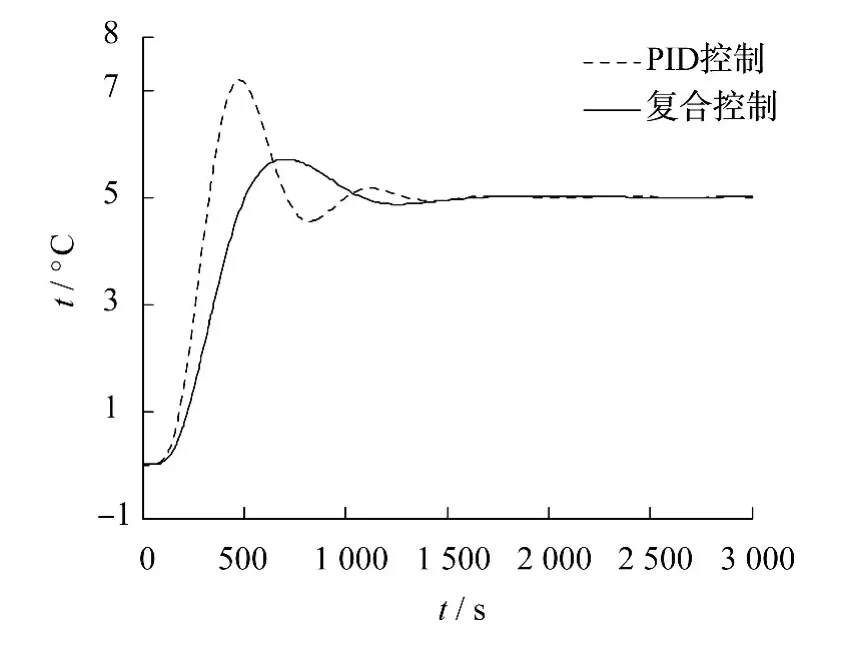
图5 时间常数偏差时的控制效果对比

通过仿真结果可知，改进型Smith预估器有较好的模型适应性，而且在模型不精确的情况下，依然能获得较好的响应特性.

将对象的增益从0.132变为0.2，而Smith预估模型保持原状不变，其控制效果如图6所示.

图6 改变对象增益的控制效果对比

由图6可以看出，传统的Smith预估器在此时已难以保证获得理想的效果，但改进后的控制器仍能保证系统有稳定的动态响应，表明此时传统的PID控制已接近不稳定.

理论上，模糊控制器可以在响应初期获得较快的响应速度，并接近设定值，而PID控制器能够保证系统有较好的跟踪设定值的能力.而在仿真过程中，实际过热汽温对象要求温度动态和稳态偏差均较小，并给PID控制器保留了较大的稳定裕量，导致系统初期响应速度比PID控制要慢，但通过模糊控制减小了系统的超调量，系统的稳定时间明显加快，而且衰减率大大增加，也就是说稳定裕量大大增强.图5可以明显看出复合模糊控制器有着较小的动态偏差、快速的调整时间及接近100%的衰减率.由此说明改进型Smith复合模糊控制器具有理想的动态特性.

4 结语

本文采用了改进型Smith预估复合模糊控制方法，仿真结果表明，该Smith预估方案有着较理想的鲁棒性，能够适应补偿模型与实际对象之间无论是时间常数还是系统增益的偏差.而模糊控制方案与PID控制器的并行控制，利用了模糊控制在大偏差时的快速性，小偏差下理想的动态特性，从而增加了PID控制器较高的稳态精度，保证了系统较好的动态和稳态特性.

［1］杨锡运，徐大平，柳亦兵，等.过热汽温多模型预测函数控制策略的研究［J］.动力工程，2005，25(4):537-540.

［2］赵峻彦.模糊控制现状与展望［J］.吉林工程技术师范学院学报:自然科学版，2006，22(9):1-4.

［3］刘红波，李少远，柴天佑.一种基于模糊切换的模糊复合控制器及其应用［J］.控制与决策，2003，18(5):12-15.

［4］金以慧.过程控制［M］.北京:清华大学出版社，1993:136-140.

［5］胡中功，宗毅，徐利新.Smith预估器的一种改进方案及其仿真研究［J］.武汉化工学院学报，2001，23(4):75-77.

［6］李旭.过热汽温的动态特性与控制［J］.动力工程，2007，27(2):199-203.