海缆布里渊光时域反射信号的去噪方法研究
柯天兵,林 琳,李永倩,翟丽娜
(1.福州电业信息科技有限公司,福州350004;2.华北电力大学 电子与通信工程系,保定071003)
引 言
光电复合海底电缆作为一种新兴海缆,具有同时输送电能和电网信息的优势,已成为海缆的主要发展趋势,在各行业逐渐得到广泛应用。在复杂的海洋环境中,海水腐蚀、海域养殖、船锚等对海缆运行造成的影响不容忽视,因此,实时监测光电复合海缆的运行状况对确保电网安全稳定运行具有十分重要的意义。采用布里渊光时域反射(Brillouin optical time domain reflectometry,BOTDR)技术监测光电复合海缆,能实现光纤沿线温度和应变的实时测量,及时发现故障点并进行准确定位。
利用BOTDR技术对光电复合海缆进行监测时,所采集的信号中会含有很多噪声,噪声的存在将严重干扰信号的本质特征。因此,在对原始信号进行预处理时,有必要对噪声加以消除或减小,以便最大程度地提取原始信号中的有用信息[1]。
本文中根据BOTDR信号特点,采用小波阈值方法对信号进行了去噪处理,并对小波阈值去噪的基础性问题,如小波基函数、分解层数、消失矩阶数和阈值方式选取方法,进行了深入研究,确定了适于光电复合海缆BOTDR测试信号去噪的最优参量。采用中值滤波法、均值滤波法和小波阈值法分别对现场获取的BOTDR测试数据进行了去噪处理。对比分析结果表明,小波阈值方法有良好的去噪效果,有利于高效地提取海缆BOTDR测试数据中的有用信息。
1 光电复合海缆的BOTDR测试信号
利用BOTDR技术对光电复合海缆监测前,对布里渊光时域反射仪的参量设置如下:脉宽10ns,叠加平均次数 213,采样间隔 1m,扫频范围10.75GHz~11GHz。在光电复合海缆在线监测系统中,布里渊光时域反射仪产生一定宽度的脉冲光入射进海缆的光纤单元,由于受线路环境等多种因素影响,产生的背向布里渊散射信号会不可避免地引入噪声,从而影响对测量信号的准确分析。测得的BOTDR信号如图1所示,其中海缆长约3500m。由图可见,海缆采集的BOTDR信号信噪比较低,有用的温度和应变信息受噪声干扰严重。由于信号的偏振特性和光纤色散等因素影响,导致接收信号包含大量噪声,如偏振噪声、相位噪声、放大自发辐射噪声等,因此需要对信号做进一步去噪处理。
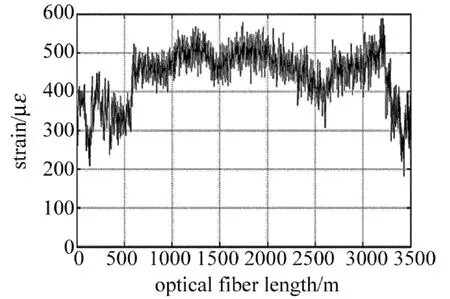
Fig.1 BOTDR monitoring signal of submarine cables
2 小波阈值去噪最优参量选取方案
在小波阈值去噪过程中,小波基函数、分解层数、消失矩阶数和阈值方式的选取对信号的去噪效果具有直接影响。选定去噪最优参量的具体方法见下。
(1)根据海缆BOTDR测试信号的特点,大致选择可行的小波基函数,利用选定的小波基函数,分别选取不同的分解层数、消失矩阶数和阈值方式,对信号进行小波分解和重构,得到去噪后信号。
(2)把测试信号的平均去噪结果作为原始信号。根据(1)式,计算上述不同分解层数、消失矩阶数和阈值方式下去噪信号的均方误差,建立不同参量设置下,去噪性能指标的对照表。
(3)从表中选择均方误差最小的一组小波基函数、分解层数、消失矩阶数和阈值方式组合方案,作为海缆BOTDR测试信号小波阈值去噪的最优参量[2]。
为了更加准确地评定去噪效果,采用均方误差(mean squared error,MSE)指标来判断去噪效果的好坏。
设原始信号为xn,去噪后信号为yn,n为信号的长度。均方误差m定义为:

均方误差代表去噪后信号与原始信号之间的相似度,MSE越小,说明相似度越高,即去噪效果越好。
2.1 小波基函数
常用的小波基函数主要有Haar,Daubechies(简写为 db),Symlets,Coiflet,Biorthogonal,ReverseBior和Dmeyer,其在正则性、紧支性、平滑性和对称性等方面的特性各不相同。目前对最佳小波基的选择还没有统一的标准[3]。通常根据小波基函数的性质和信号的特点,凭经验选择最佳小波基。
2.2 分解层数和消失矩阶数
分解层数对于消噪效果的影响很大。若分解层数过多,并对各层小波系数都进行阈值处理,会造成有用成分丢失严重,消噪后的信噪比下降。分解层数过少则去噪效果不理想,信噪比提高不多。因此需要确定一个合适的分解层数才能取得较好的去噪效果。
消失矩阶数决定了小波逼近光滑信号的能力[4]。理论上选择较高阶的消失矩,能有效突出信号的高频细节。
图7是炉排调风门全开时的风室静压分布情况,右侧为风室进口,左侧为风室尾部。从图7中可以看到,风室进口静压小,尾部静压大,静压分布呈阶梯型分布。这是由于在风室中,由于流量分配及沿程阻力损失等因素的影响,沿工质流向空气流速逐渐减小,动能逐渐转为压力能,导致风室进口风压较小,尾部风压大。鉴于此,需要增大进口风门开度,减小尾部开度。
2.3 阈值方法
阈值处理方法主要分为硬阈值和软阈值方法。硬阈值法是将分解后信号的绝对值和阈值比较,大于阈值的小波系数保持不变,小于或等于阈值的小波系数则置为0。软阈值法是将小于阈值的小波系数置0,大于阈值的小波系数变为该小波系数与阈值的差值[5]。
软阈值选取主要有 sqtwolog,rigrsure,heursure及minimaxi 4种规则。sqtwolog规则采用固定阈值,去噪效果较明显,但阈值风险较大;rigrsure规则需计算给定阈值的似然估计,然后将非似然最小化,得到所选阈值;heursure规则综合了前两种阈值规则的优点,是最优预测阈值,主要用于信噪比很低的场合;minimaxi规则产生一个最小均方差的极值,极值估计可以在一个给定的函数集中实现最大均方误差最小化[6]。
3 实验及分析
3.1 最优小波基函数选取
对于BOTDR信号,大多数文献中都采用db小波基进行小波阈值去噪。HE[7]等人采用db小波基的小波阈值方法对BOTDR信号进行去噪,结果表明,小波阈值能有效去除噪声。QIN[8]等人采用db小波基的阈值方法对120m光纤采集的BOTDR信号进行去噪处理,取得了良好效果。XU[9-10]等人利用db小波基的阈值方法对300m光纤的BOTDR信号进行了消噪处理,并用模极大值法检测信号的异常值,结果表明此方法适合处理BOTDR测试信号。db小波具有正交性、正则性,紧支性,对非平稳信号较灵敏,适宜在时域上做局部分析。基于理论和前人的经验,本文中采用db小波基函数对海缆BOTDR测试信号进行去噪处理。
3.2 最优分解层数和消失矩阶数选取
基于上述理论,在db小波基下,分别用1~8不同分解层数,1~10阶不同消失矩阶数对海缆BOTDR测试信号进行小波阈值去噪,去噪后信号的MSE值如表1所示。
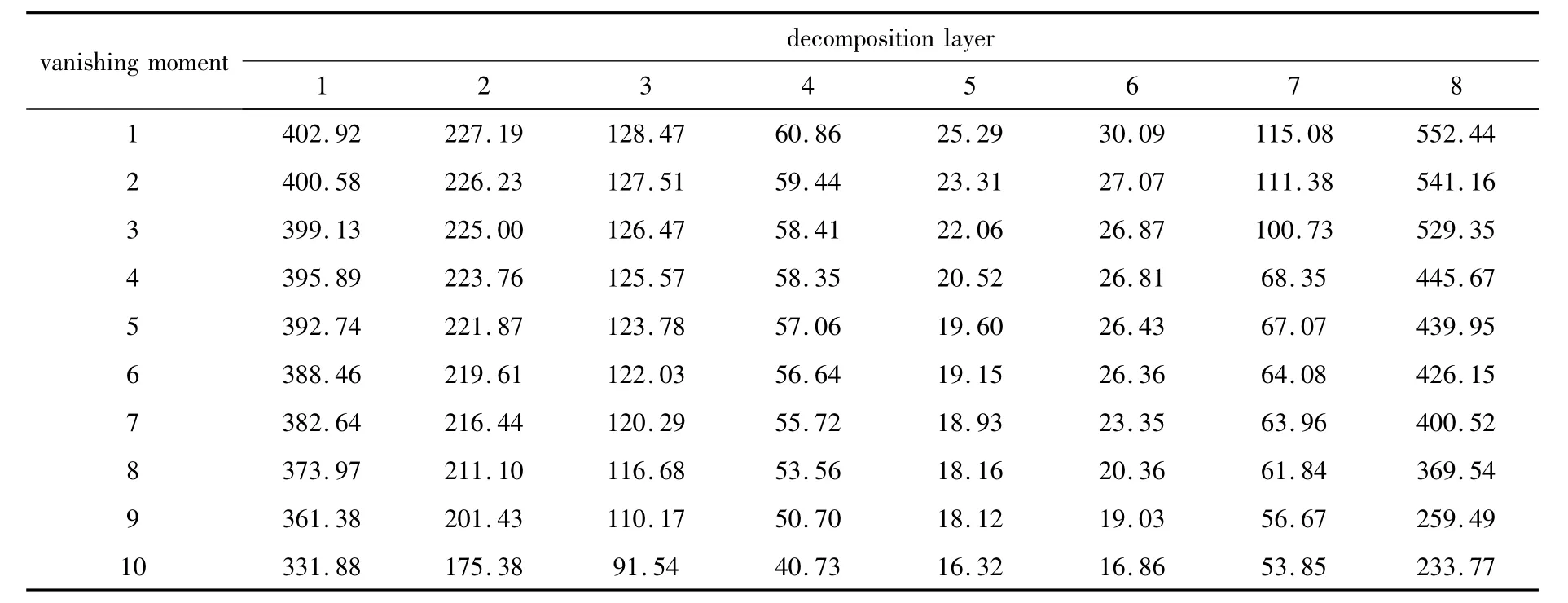
Table 1 MSE of denoised signal with different parameters
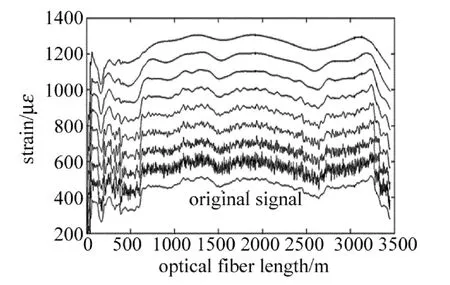
Fig.2 Denoised signal with different decomposition layer and the same vanishing moment
由表1中数据可见,当消失矩阶数相同时,在1层~5层随着分解层数的增加,均方误差逐渐减小;当达到6层分解时,均方误差又呈上升的趋势。图2中给出了不同分解层数下小波去噪波形,图中曲线从上到下依次为8层分解~1层分解下去噪后信号,最底层曲线为原始信号,由图中曲线可见,当分解层数为5时,既能有效去除信号中的无用成分,相对其它分解层数又最完整地保留了有用成分。分解层数增加到6层及以上,去噪效果变差,并且增加了计算代价。显然,对于光电复合海缆的BOTDR监测信号,5层分解去噪效果较为理想。
当分解层数为5时,随着消失矩阶数的增加,均方误差逐渐减小,在其它分解层数时,消失矩和均方误差之间有同样的变化规律,即10阶消失矩时均方误差最小。图3为5层分解时1阶~10阶不同消失矩下的信号去噪曲线,曲线从上到下依次为10阶消失矩~1阶消失矩下去噪信号,最底层曲线为原始信号,由图中曲线可见,10阶消失矩时去噪信号和原始信号几乎具有相同的特征和变化趋势,且和其它消失矩阶数对应曲线相比,更能突显信号的细节部分,因此选用10阶消失矩。
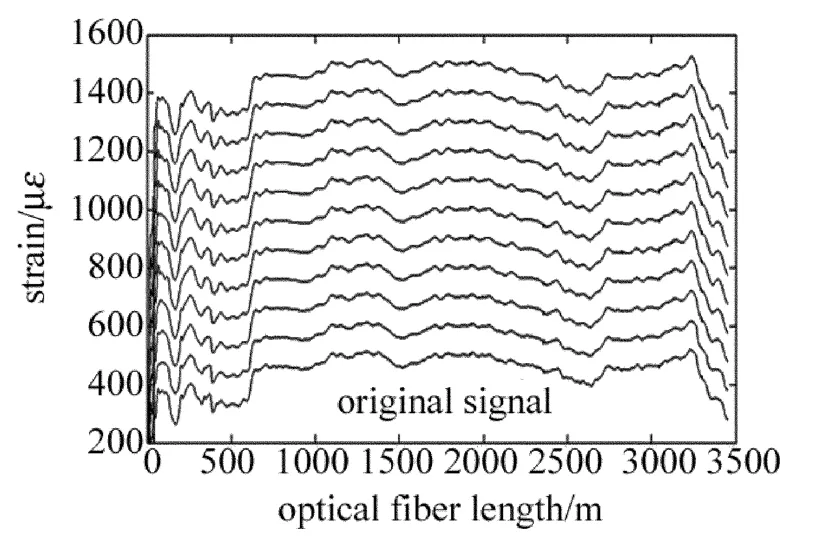
Fig.3 Denoised signal with different vanishing moment and five decomposition layers
3.3 最优阈值方法的选取
选定db10和5层分解后,分别对硬阈值和软阈值下去噪信号的波形进行了对比分析,如图4所示。
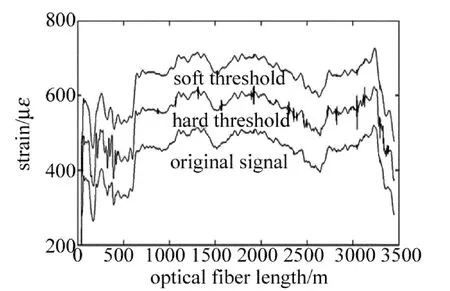
Fig.4 Denoised signal with hard threshold and soft threshold
由图4可见,软阈值处理后的信号较硬阈值平滑,去噪效果更为理想,因此选定软阈值处理方法。
在db10,5层分解和软阈值基础上,对4种不同阈值规则下去噪信号进行了对比,如图5所示。
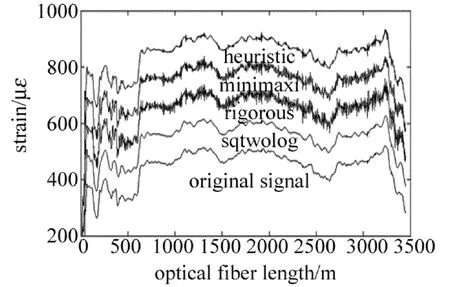
Fig.5 Denoised signal with different threshold regulation
在 sqtwolog,rigrsure,heursure和minimaxi 4 种阈值规则中,信号去噪后信噪比分别为38.993dB,31.374dB,38.348dB 和32.836dB。结合 图 5 可知,sqtwolog和heursure去噪比较彻底,rigrsure和minimaxi阈值选取规则较为保守,阈值较小,噪声去除不彻底。相对来说,sqtwolog阈值规则去噪最彻底,去噪后信噪比最高,因此选取sqtwolog固定阈值规则。
综上所述,对于光电复合海缆采集的BOTDR信号,用小波阈值去噪选取的最优参量为:db小波基、10阶消失矩、5层分解、软阈值和sqtwolog固定阈值规则。在此参量下对信号进行去噪后信噪比达到了38.993dB。相比于去噪前信号24.794dB的信噪比,提高了14.199dB。
4 最优参量验证
4.1 最优参量的合理性分析
上述最优去噪参量的选取是通过MSE指标进行衡量的,在实际光电复合海缆实时在线监测中,有必要对最优参量的合理性进行检验。检验此参量合理性的步骤见下。
(1)在海缆测试曲线某段平坦的波形处增加一定程度的应变。
(2)在最优参量设置下对信号进行去噪,看能否将此处的应变检测出来,若能检测出来,则说明此参量是合理的。
通常光纤受到约10g作用力时,其应变变化100με。因此选定海缆波形中2001m~2020m处平坦的20m,人为增加100με的应变,信号如图6中实线所示,图中所加的100με应变被淹没在噪声中。采用db小波基、10阶消失矩、5层分解、软阈值和sqtwolog固定阈值规则去噪后,波形如图6中虚线所示。从图中可以清楚地观察到2001m~2020m处骤增的100με应变,即在该参量下的小波阈值去噪能检测出100με的应变变化,亦能检测出应变变化大的船锚等人为损坏造成的海缆应变变化。可见此参量设置是合理的。
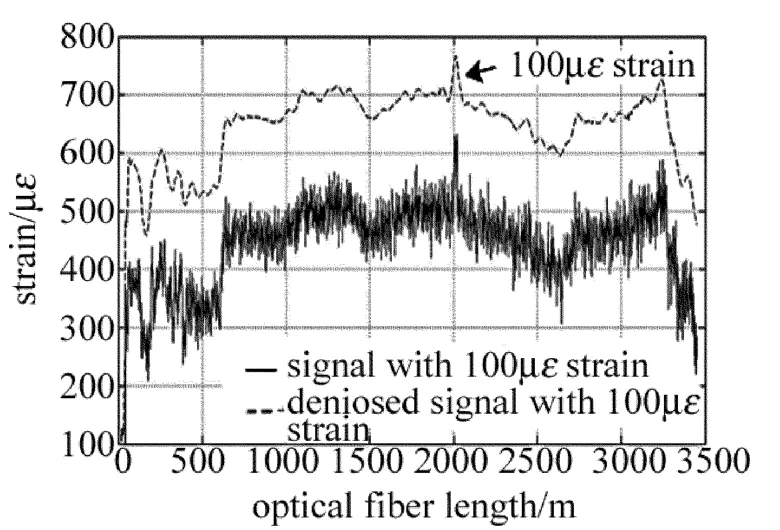
Fig.6 BOTDR signal with increased strain
4.2 和其它去噪方法对比
传统的去噪方法主要有均值滤波法和中值滤波法等,其和小波阈值法的对比如图7所示。

Fig.7 Comparison of wavelet threshold denoising with mean filtering and median filtering
由图7可看出,中值滤波可以保护信号尖锐边缘,但其去噪效果依赖于滤波窗口的大小[11-12]。当窗口小时,信号去噪不彻底;当窗口大时,则导致信号失真。均值滤波速度快、算法简单,但去噪时一部分有用信号被当作噪声滤除。可见传统的滤波方法不能很好地刻画信号边缘、尖峰、断点等非平稳特性,不能达到有效去除噪声、提取有用信号的目的。小波阈值法既能有效去除噪声,也能很好地保留有用信号中的尖峰和突变部分,适于海缆BOTDR测试信号的去噪处理。
5 结论
利用小波阈值法对BOTDR测试信号进行了去噪处理。根据实际测试信号的特点,分析了小波基函数、分解层数、消失矩阶数和阈值方式的选取方法,并以均方误差作为评价指标,选定了一组较合理的小波阈值去噪参量,即db小波基、10阶消失矩、5层分解、软阈值和sqtwolog固定阈值规则,作为最优参量。为验证最优参量的合理性,人为地在海缆测试曲线某平坦段增加100με应变,并和中值滤波、均值滤波方法进行了对比。实验结果表明,在设置的最优参量下进行小波阈值去噪能有效消除噪声和提取海缆特征点等有用信息,能检测出100με的应变变化。本研究对于海缆BOTDR监测信号的高效处理具有重要参考价值。
[1] GUO Ch Y,ZHENG K.Denoising optical interferometry signal based on wavelet transform threshold[J].Laser Technology,2009,33(5):506-508(in Chinese).
[2] WANG X W,DONG G B,XIE G H.A new de-noising method of NMR FID signals based on wavelet transform[J].Nuclear Electronics& Detection Technology,2008,28(2):365-370(in Chinese).
[3] LIU B,WU Y F,ZHAO X C.Research on wavelet selection in all fiber displacement interference speed measurement system[J].Laser Technology,2012,36(2):251-254(in Chinese).
[4] WU Y.The study of the method based on wavelets in signal denoising[D].Wuhan:Wuhan University of Technology,2007:1-63(in Chinese).
[5] LU E Z,ZHANG Ch.Method and model setup of wavelet denoising in on-line monitoring systems[J].Electrotechnical Application,2006,25(5):93-95(in Chinese).
[6] CUI Zh.The research and application of wavelet analysis in ultrasonic signal processing[D].Hunan:Hunan University,2012:1-73(in Chinese).
[7] HE J P,ZHOU Zh,CHEN G D,et al.Measurement accuracy improvement of Brillouin signal using wavelet denoising method[J].Proceedings of SPIE,2009,7293:72930B.
[8] QIN Sh W,GU Ch.Principle and application of BOTDR and wavelet processing of its signal[J].Mechatronics,2008,14(11):54-56(in Chinese).
[9] XU H Zh,SHI B,ZHANG D,et al.Signal processing of the fiber optic BOTDR sensor based on wavelet analysis[J].Journal of Optoelectronics·Laser,2003,14(7):737-740(in Chinese).
[10] XU H Zh,ZHANG D.Wavelet-based data processing for distributed fiber optic sensors[C]//Proceedings of the Fifth International Conference on Machine Learning and Cybernetics.New York,USA:IEEE,2006:4040-4045.
[11] WEI Y F,DU Zh Ch,YAO Zh Q.Application of median filter in point cloud data pre-processing lidar[J].Laser Technology,2009,33(2):213-216(in Chinese).
[12] WANG D W,WANG G L.Application of adaptive median filtering in cloud Doppler radar data pre-processing[J].Laser Technology,2012,36(2):221-224(in Chinese).

