异轴角散射法测量湿蒸气参量的方法研究

杨 颖，黄竹青，2*，曹小玲

(1.长沙理工大学能源与动力工程学院，长沙410114;2.湖南有色金属职业技术学院，株洲412006)

引 言

湿蒸气对汽轮机的影响主要有两点，一是汽轮机末级蒸汽凝结过程中产生的热力学损失及其形成水滴使汽轮机组效率降低，也就是湿气损失;二是蒸汽流动过程中形成的高速水滴使汽轮机末级叶片产生水蚀，甚至断裂。因此，实时监测汽轮机末级湿蒸气中水滴大小分布和浓度的变化，对汽轮机的安全经济运行和指导锅炉给水有着重要的意义。针对该问题，经过参考分析［1-3］，本文中提出一种测量湿蒸气参量的异轴角散射方法，并对该方法进行仿真分析和实验研究。

1 测量原理

异轴角散射法［4］是通过光电探测器采集散射立体角θ1～θ2范围内的散射光能来实现的。本文中提出的实验模型如图1所示。激光光束进入湿蒸气到达探测器先后经历衰减、散射、衰减3个过程，这3个过程分别遵循Lambert-Beer定律、Mie散射理论和Lambert-Beer定律。

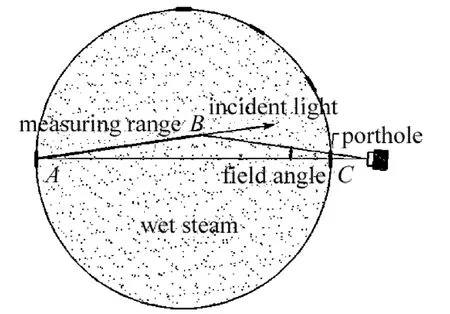
Fig.1 Experimental model

1.1 数学模型

在整个研究过程中，假设衰减区和散射区水滴分布均匀，水滴群中的各个水滴是相互独立的散射体，各个水滴之间的散射光互不相关，所以水滴群的散射特性是散射区域内各个水滴散射特性的线性叠加。作者以适合描述破碎形成的微粒群的Rosin-Rammler分布函数表示水滴群的尺寸分布，其尺寸分布概率密度函数表达式为［5］:

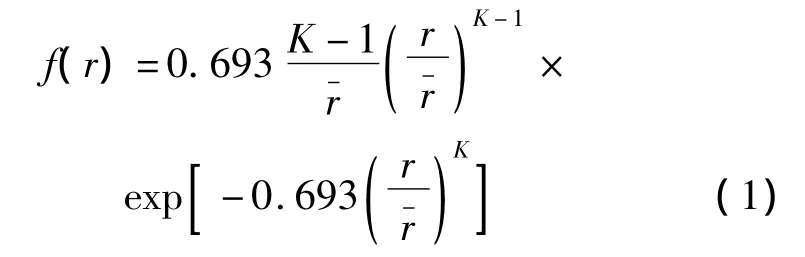
式中，r为半径，r－是质量中间半径，K是尺度分布参量，设入射激光光强为I0，到达散射区之前的光程为L01，散射区长度为L，散射区和出光孔之间的距离为L02。理论公式推导如下:

衰减区L01:

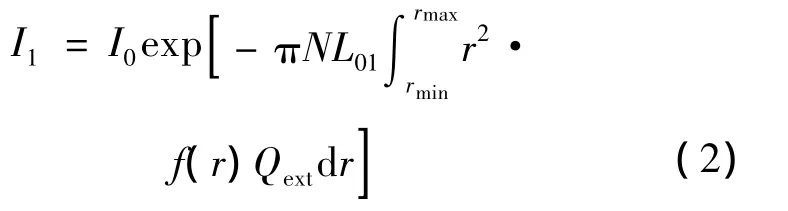
散射区:

式中，Qext是消光系数，由Mie系数求得;dS是像元对应的散射区面积;N是单位体积内粒子个数，即水滴浓度;Is是单个粒子在散射立体角内的散射光强，表达式为:

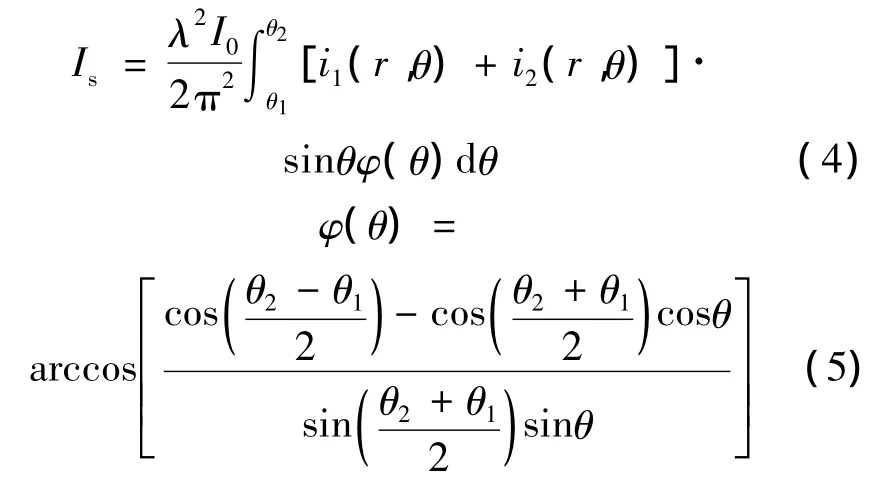
式中，i1(r，θ)和i2(r，θ)是散射强度函数，由 Mie 散射理论求得，φ(θ)是极化角和散射角之间的关系。为了提高Mie散射理论的计算精度和运算速度，采用LENTZ改进的连分式［6］方法和向前递推［7-8］计算Mie系数。

衰减区L02:

综合(1)式～(6)式，得到散射比:

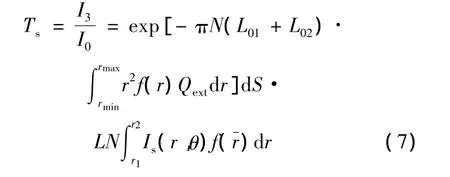
1.2 参量计算

测量装置主要由蒸汽发生器、激光器、CCD光电探测器［9-11］组成，成像光路如图2所示，散射微元和接收截面组成散射立体角，经过镜头成像于对应的像元。

Fig.2 Schematic diagram of imaging

首先使激光光束通过汽缸的水平直径与CCD靶面中垂线重合，然后将激光光束逆时针旋转，CCD按接收截面中垂线顺时针旋转，旋转角度分别为b和β，O是CCD相机镜头所在位置，由CCD相机配合镜头的视场角φ结合有效像元个数n将散射区域AN平均划分为n个相对应的散射区，BM是垂直于AF的辅助线，根据图3得到如下关系:

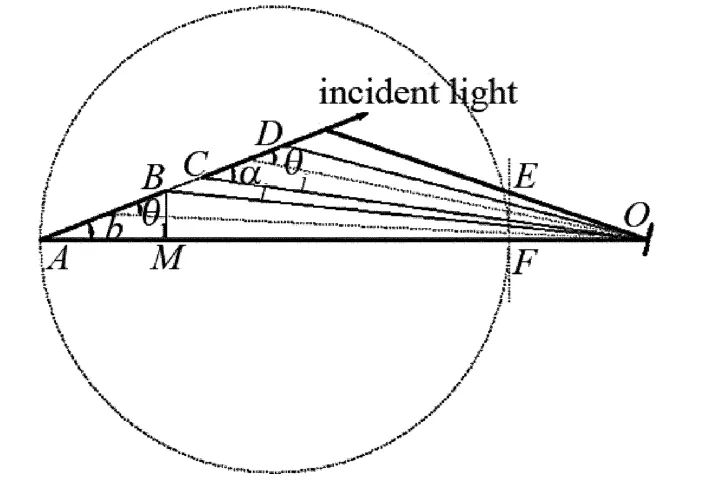
Fig.3 Schematic diagram of receiving structure

式中，n是有效像元个数，Lj是像元j所对应的散射区长度(如AB，CD等)，L01，j和L02，j是像元j所对应的衰减区长度(如AC，DE)，θj和 αj分别是像元j所对应的平均散射角和接收立体角的起始角度。

散射立体角的计算如图4所示。CD是接收截面，B是某一像元对应的散射区，DE是垂直于OB的辅助线，散射立体角的范围为θj±Δθ，Δθ与接收截面的大小和θj有关，计算过程如下:

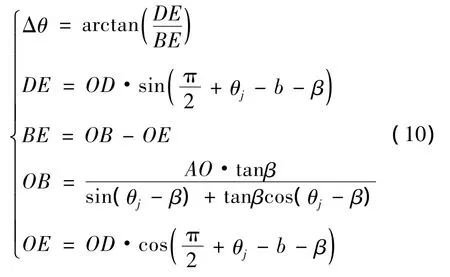
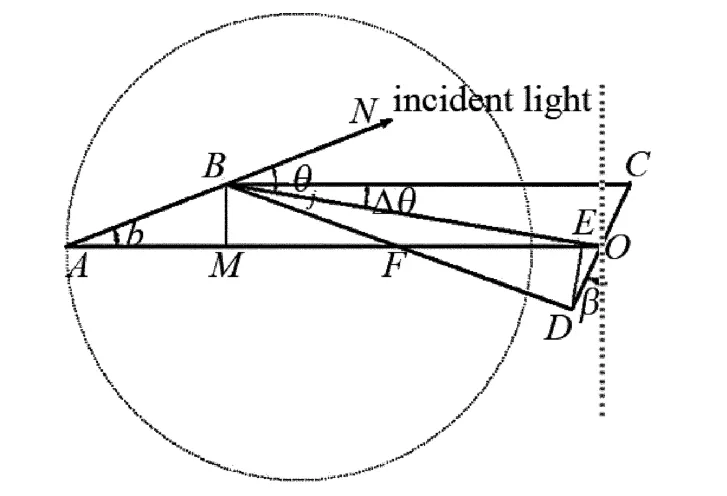
Fig.4 Schematic diagram of the scattering structure

根据实验仪器的具体参量，Lj，L01，j，L02，j和散射立体角变化规律如图5所示。

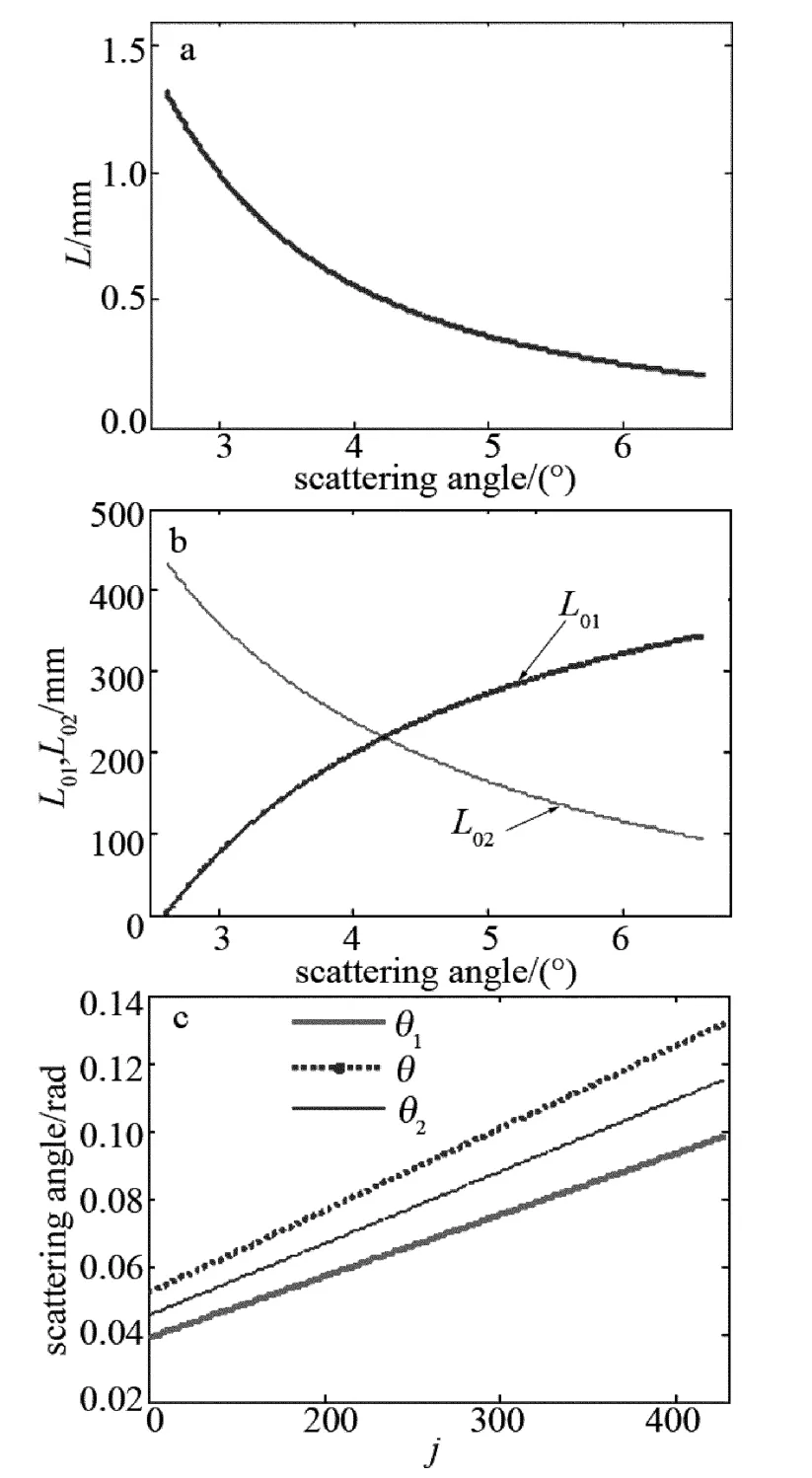
Fig.5 a—variety of scattering region varying along with angle b—variety of attenuation region varying with angle c—variety of scattering solid angle varying with j

2 仿真与实验分析

2.1 实验参量与仿真

主要实验仪器参量:模拟汽缸直径为437mm，激光波长λ=0.532μm，功率为0mW～100mW连续可调;CCD探测器分辨率为656pixel×493pixel，镜头焦距为75mm，视场角为4°，折射率m=1.33。实验测量时，将激光光束逆时针旋转2.6°，CCD按接收截面中垂线顺时针旋转2°。结合实验仪器的参量和(7)式进行仿真，得到改变质量中间半径r－、尺度分布参量K、水滴数浓度N对散射比的影响规律(见图6)。由仿真结果可知:(1)随着角度的增加，散射比非线性地减小;(2)水滴浓度N和尺度分布参量K不变的情况下，质量中间半径r－增大，散射比增大，且随着散射角度的增加变化越快;(3)尺度分布参量K越大，水滴群的半径就越集中，表现出单一分散系的振荡特性，散射比随角度的变化越快;(4)水滴浓度N增加，散射区内水滴数量增多，散射比增大。

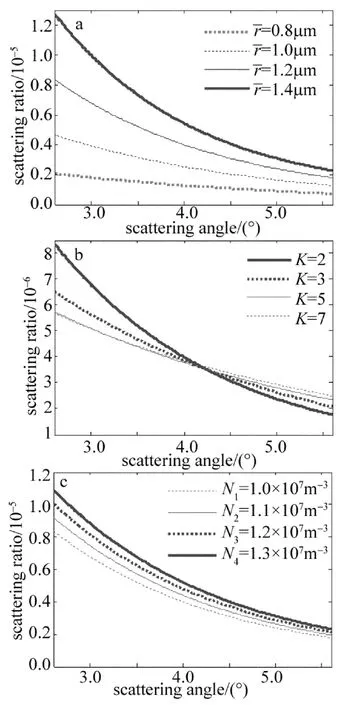
Fig.6 Analysis of the mock result

2.2 实验结果

根据理论模型设计实验，测量出不同工况(见表1)下的散射信号，转变成灰度图像(见图7)，并对其进行中值平滑滤波，由于CCD像元灰度在接收到的光强未达到饱和时，像元灰度值与光强呈线性关系［12］，即像元灰度值越高，像元上接收到的散射光强越大，因此，可以用灰度值随角度的变化趋势表示散射光强的变化趋势。

Table 1 Different condition of parameters setting

Fig.7 Gray-scale diagram of different conditions

取灰度图像中线上3.6°～5.6°对应的灰度值，如图8所示:像元灰度值随角度的变化呈下降趋势;不同工况时得到的图片灰度值不同，随着汽缸背压的减小，对应的像元灰度值增大，这是因为模拟汽缸内的湿蒸气随着背压的下降，焓降增加，蒸汽湿度增大。蒸汽湿度跟水滴半径和水滴数浓度有关，湿度越大，水滴半径或水滴数浓度就越大;实验数据的变化趋势和仿真分析的结果基本一致。表1为不同工况的参量设定。

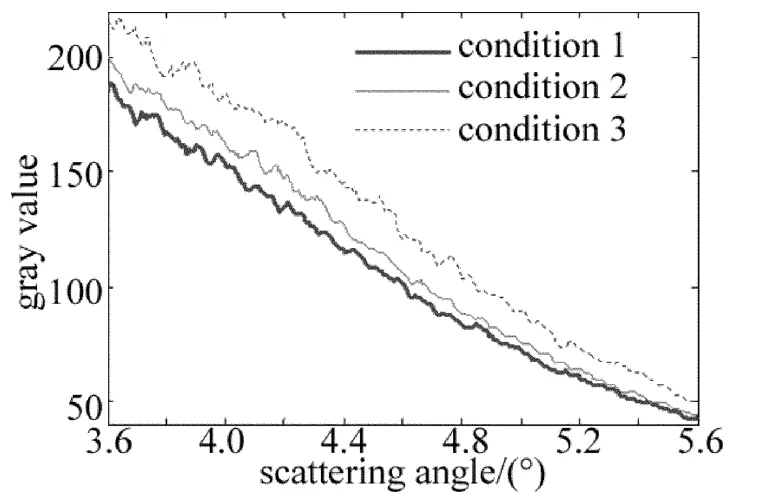
Fig.8 Variety of gray-scale value corresponding to different conditions varying with angle

3 结论

采用异轴角散射法，以CCD作为散射光探测器进行实验研究，通过仿真和实验数据的比较，实验数据的变化趋势符合仿真分析的结果;另外，如果以正常状态下微粒群的灰度图像作为标准，实时测量的数据和标准图像作比较，就能够快速地得出微粒群参量的变化趋势。所以本文中所提出的测量湿蒸气参量的方法是可行的。该方法还能应用到煤粉、空气质量等微粒群的测量上。

［1］ HUANG Zh Q，YANG J M，SUN C Sh，et al.Application of the laser scattering theory for monitoring steam wetness and droplet size in steam turbines［J］.Journal of Power Engineering，2006，26(2):241-244(in Chinese).

［2］ ZHOU L X，ZHANG M Zh，WANG S L，et al.Situation and development of steam wetness measurement in turbine exhaust casing［J］.Journal of North China Electric Power University，2001，28(2):72-76(in Chinese).

［3］ WANG L L，CAI X Sh.Progress in research on water droplet size in two phase wet steam flow in steam turbine［J］.Journal of University of Shanghai for Science and Technology，2003，25(4):307-311(in Chinese).

［4］ HUANG T L，ZHENG G，WANG N N.Theory study of light scattering measurement technology on particulate contamination under ultraclean environment［J］.Journal of Guilin Institute of Electronic Technology，2000，20(1):6-12(in Chinese).

［5］ ITO S.Optical wave propagation in discrete random media with large particles a treatment of the phase function［J］.Applied Optics，1993，32(9):1652-1656.

［6］ LENTZ W J.Generating Bessel funtions in Mie scattering calculations using continued fractions［J］.Applied Optics，1976，15(3):668-671.

［7］ DAVE J V.Coefficients of the legendre and Fourier series for the scattering functions of spherical particles［J］.Applied Optics，1970，9(8):1888-1896.

［8］ BAYVEL L P，JONES A R.Electromagnetic scattering and its applications［M］.London，UK:Applied Science Press，1981:26-27.

［9］ ZHANG B D，QIN Sh Q，JIA H J，et al.Measurement model and uncertainty analysis of pulsed laser far field energy density based on CCD imaging［J］.High Power Laser and Particle Beams，2008，20(9):1417-1920(in Chinese).

［10］ ZHONG J，WENG J D，LUO Zh X，et al.Study on stray facula of array CCD detector irradiated by laser pulse［J］.Laser Technology，2010，34(6):835-838(in Chinese).

［11］ SU P，NIU Y X，LI D Q，et al.Image acquisition and processing of a laser warning system based on planar array CCD［J］.Laser Technology，2013，37(3):394-399(in Chinese).

［12］ WANG Q Y.Application technology of CCD［M］.Tianjing:Tianjing University Press，2000:17-27(in Chinese).