可用于传感领域的环形谐振腔游标效应的研究

赵 宇，马可贞，杨德超，郭泽彬，张文栋，薛晨阳，闫树斌

(中北大学仪器科学与动态测试教育部重点实验室，太原030051)

引 言

基于谐振腔的游标效应［1］，可以拓宽有效自由频谱宽度(free spectral range，FSR)调节范围，在光开关、滤波器、可调谐激光器及传感器等领域已得到了广泛的应用。2002年，GEUZEBROEK 等人［2］利用环形谐振腔级联的游标效应拓宽FSR，得到可以对第3方通信窗口波长进行选择的热调谐宽频FSR光开关。2005年，CHOI等人［3］在可调谐窄线宽全掩埋异质环形谐振腔滤波器的实验中，利用掩埋异质环形谐振腔的游标效应来扩大FSR和谐振波长的调谐范围，谐振时 D端口输出的有效 FSR从0.65nm 延长到10.2nm，谱线宽度为 0.017nm，测量的精细度高达600。2008年，HE等人［4］利用半波V型耦合腔的游标效应克服了材料本身增益的变化，通过实现有效折射率的变化，极大地增加了波长可调谐半导体激光器的可调谐波长范围。2010年，BOECK等人［5］利用跑道型谐振腔的游标效应降低弯曲损耗来增加自由频谱范围，从而使多路复用器的自由频谱范围延长了36nm，增加了频道数量。此外，游标效应在生化传感领域也取得了新进展，2011年，浙江大学JIN等人［6］利用双级联环形谐振腔的游标效应取代窄线宽可调谐激光器和高精度的光学频谱分析仪(optical spectrum analyzer，OSA)来提高有效折射率在生物传感器中的测量精度，实验表明，随着溶液浓度的变化，测量的精度达到1300nm/RIU(refractive index unit)。近年来，环形谐振腔的研究越来越热［7］。光纤环形谐振腔因具有高谐振特性、结构简单、稳定可靠等优点成为光学传感的重要器件，引起了广泛关注。同时，随着微机电系统加工技术的不断发展，光波导材料制备技术也逐渐成熟，光波导环形谐振腔的小型轻量、低耗高效、高集成度等特性，使其在集成光学领域具有广阔的应用前景［8-9］。

本文中分别对光纤环形谐振腔的谐振原理、游标效应进行了深入的实验研究。通过改变环形谐振腔的光程差(改变尺寸差或折射率)，得到提高测量精度的方法。

1 实验原理

1.1 光纤环形谐振腔的原理

与F-P腔不同，光纤环形谐振腔(fiber ring resonator，FRR)用低损耗光纤代替光学腔，用光纤耦合器代替反射镜，减小了传输光在耦合区的损耗并且降低了谐振腔的加工制作难度，具有结构简单、带宽窄、高分辨率、高品质因数(Q值)、低损耗等特性［10-13］。图1是光纤环形谐振腔的光场示意图。

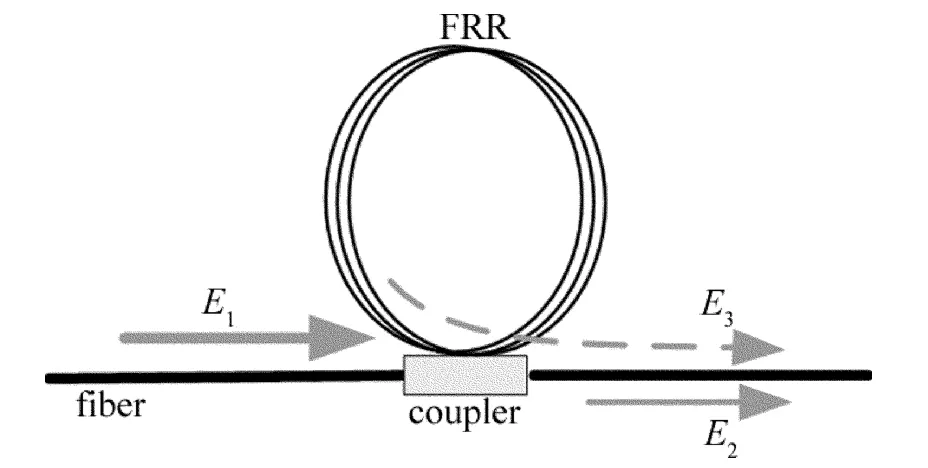
Fig.1 Schematic diagram of light field of a fiber ring resonator

光纤环形谐振腔的输入光场可以表示为［14］:

式中，E1是光纤环形谐振腔输入光场的幅度值;f为激光器的中心频率;φ0为初始相位。从耦合器直接输出的光场为［14］:

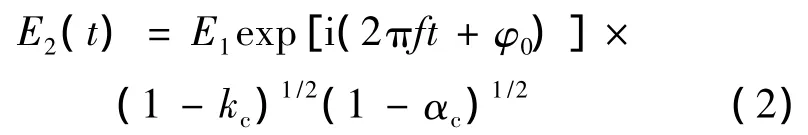
式中，kc，αc分别为耦合器的耦合系数和损耗系数。经过推导，在光纤环形谐振腔中环绕多次后通过耦合器的输出的光场可以表示为［14］:

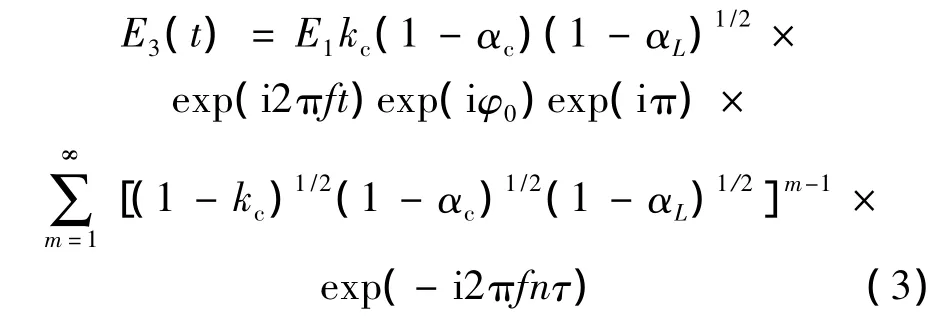
式中，αL为光场在光纤环形谐振腔中传输一次的损耗系数，τ=nL/c(c代表光速;L代表环形谐振腔的腔长)为激光在光纤环形谐振腔中传输一次所需时间，光场经过一次耦合器相位突变为π/2。光纤环形谐振腔的总输出光场是E2和E3之和，表示为:

经推导，光纤环形谐振腔的传递函数为:

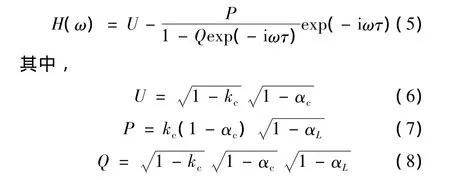
图2为光纤环形谐振腔的谐振谱线。光纤环形谐振腔的FSR(=c/(nL))指相邻两个谐振波谷的间距［15-16］，为94MHz。相关的实验参量为:光纤环形谐振腔的长度L=2.24m;光纤的折射率n=1.45;耦合器耦合系数kc=10%;耦合器的损耗系数αc=6.6%;光纤环形谐振腔的损耗系数αL=1.14%。

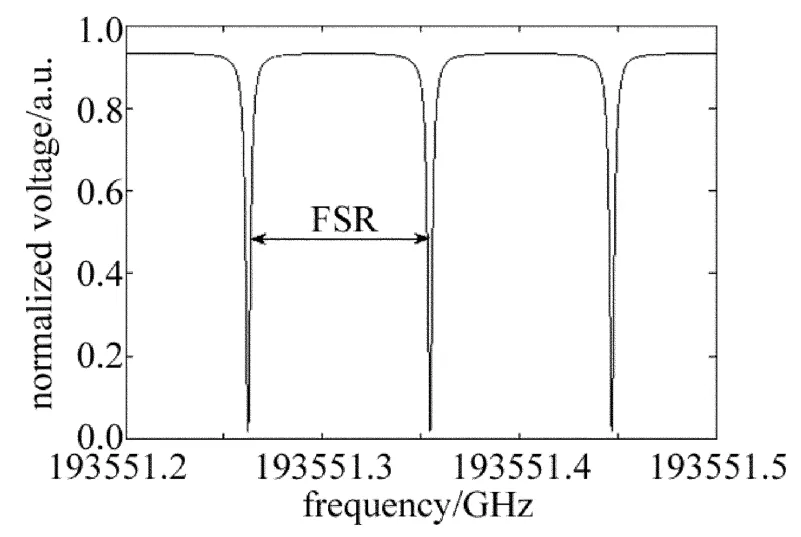
Fig.2 Spectrums of a fiber ring resonator

1.2 光纤环形谐振腔的游标原理

基于光纤环形谐振腔谐振效应及游标卡尺测量机理，设计不同长度的光纤环形谐振腔，以其中一个作为标尺，另一个作游尺，可以实现一定频率差或波长差的精确测量。实验中选取了长度分别为L1=2.24m，L2=2.52m 的光纤环形谐振腔，两个谐振腔对应的FSR分别为F1和F2，利用MATLAB软件仿真得到的基于光纤环形谐振腔的游标效应，如图3所示(仿真时，为方便说明问题，把其中一个环形谐振腔的透射谱线设置为反向)。

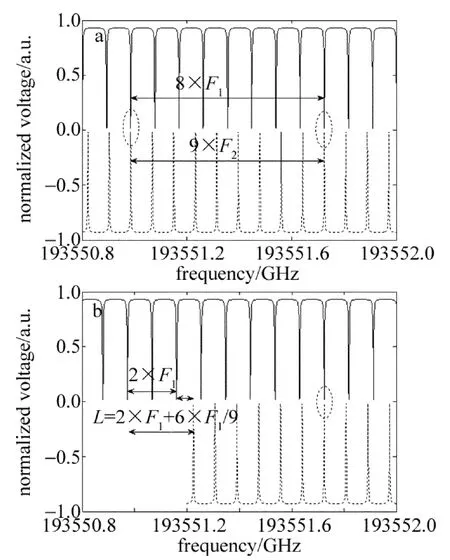
Fig.3 Vernier effect schematic of fiber ring resonator

从图3a可以看出，两个不同光纤环形谐振腔相同的频段内FSR个数满足:

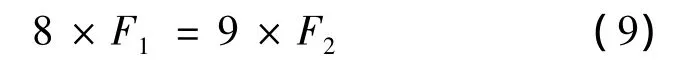
游标卡尺测量的精度的计算原理为:若游尺上m个等分刻度的总长度与标尺上(m－1)个等分刻度的总长度相等，且游尺的最小刻度长为x，标尺的最小刻度长为y，则:

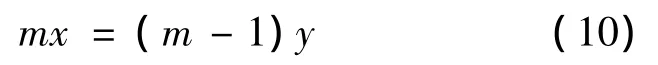
游标卡尺的测量精度为:

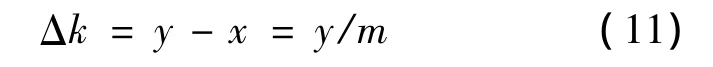
则标尺读数作为整数部分，可以读出有两个F1;游尺读数作为小数部分，其第3个谐振点与标尺谐振点对齐，测量结果为:

2 实验

2.1 实验系统搭建

为研究光纤环形谐振腔的游标效应，搭建的实验系统如图4所示:New Focus窄线宽可调谐激光器(中心波长为1550nm，线宽小于300kHz)作为光纤环形谐振腔的光源;谐振腔一端经过分束器与激光器输出端相连，另一端经光电探测器将光信号转变为电信号，用示波器来显示光电探测器输出的电信号;信号发生器产生的三角波通过对激光器的压电陶瓷施加线性变化的电压，实现对激光器的频率调制，进而得到系统的谐振谱线。

Fig.4 Schematic diagram of the experimental system

2.2 实验结果与分析

实验参量设置如下。信号发生器为三角波、VPP=0.5V(电压峰峰值)，f=100Hz;光纤环形谐振腔的长度分别为L1=2.24m和L2=2.52m。图5为在三角波信号调制下，光纤环形谐振腔的输出谱线。

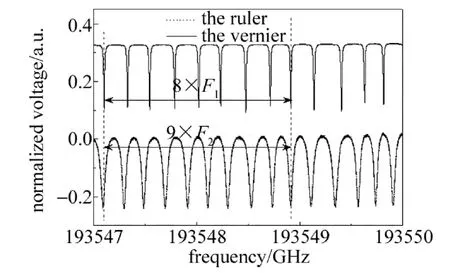
Fig.5 The diagram of the resonance spectrums of the experimental system(at the same resonant frequency band and FSR number ratio of 8∶9)

从图5可以看出，在相同的频段内，光纤环形谐振腔的FSR满足:

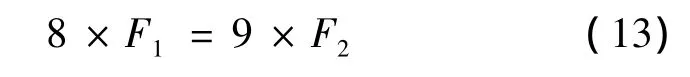
对标尺的FSR等分，则游尺测量精度为F1/9，与MATLAB理论仿真结果相一致。经计算，光纤环形谐振腔标尺F1=94MHz，则游尺的测量精度为:

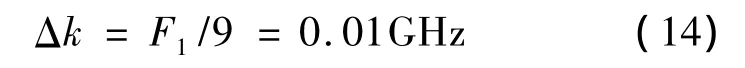
同时，从图中可以得到，标尺频谱的半峰全宽为0.009GHz，游尺频谱的半峰全宽为 0.046GHz。经计算，两个光纤环形谐振腔的品质因数分别为:Q1≈2.1 ×107，Q2≈4.2 ×106。则改变光纤环形谐振腔的长度，不仅使频谱的半峰全宽变大，同时降低品质因数。

在实验过程中，为避免振动、噪声、温差等外界环境对谱线稳定性的影响，应该把实验系统置于密闭恒温环境。

针对实际需求，可以设计不同长度差的光纤环形谐振腔，把谐振腔自由频谱宽度个数比设计为不同值(49∶50，99∶100，999∶1000)，对 FSR 差值进行50，100甚至1000等分，可以极大提高游尺测量精度，避免直接等分带来的误差。例如:标尺谐振腔F1=60pm，所需游尺测量精度为6pm，即差值需要对标尺谐振腔的一个FSR进行十等分，根据:

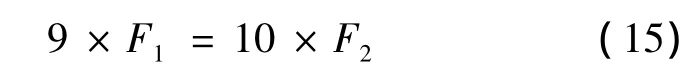
则所设计游尺谐振腔的F2=54pm，根据公式:

式中，λ为所测波段的中心波长，neff为有效折射率是常数，进而得到应设计的游尺谐振腔腔长。测量精度要求越高，两个光纤环形谐振腔的尺寸差越小。当谐振腔尺寸差要求无法满足时，可以考虑利用不同掺杂类型的光纤，通过改变有效折射率来提高测量精度。

光纤环形谐振腔可以灵敏感应外界环境的变化(如温度、压力等)，使游尺谐振谱线发生移动，结合标尺和游尺读取测量结果，建立频率与外界变化量的关系，可用作温度、压力传感器等。

3 结论

基于光纤环形谐振腔的游标效应，对其原理进行分析并利用MATLAB软件仿真。选取光纤环形谐振腔的长度分别为L1=2.24m，L2=2.52m。当频率相同时，谐振点对齐频段内FSR个数比值为8∶9，以其中一个谐振谱线作为标尺，另一个作为游尺，对标尺一个 FSR九等分，得到游尺的测量精度为F1/9，与理论仿真结果相一致。在此基础上，提出了改变谐振腔腔长差(ΔL)或折射率，增加FSR等分刻度数，来提高游尺的测量精度，为基于高精度频率差传感器的研究提供了一种有效方案。

［1］ TOBING L Y M，LIM D C S，DUMON P，et al.Finesse enhancement in silicon-on-insulator two-ring resonator system ［J］.Applied Physics Letters，2008，92(10):101122.

［2］ GEUZEBROEK D H，KLEIN E J，KELDERMAN H，et al.Thermally tuneable，wide FSR switch based on micro-ring resonators［DB/OL］.(2002-12-09)［2013-11-08］.http://purl.utwente.nl/publications/58195.

［3］ CHOI S J，PENG Zh，YANG Q，et al.Tunable barrow linewidth all-buried heterostructure ring resonator filters using vernier effects［J］.IEEE Photonics Technology Letters，2005，17(1):106-108.

［4］ HE J J，LIU D.Wavelength switchable semiconductor laser using half-wave V-coupled cavities［J］.Optics Express，2008，16(6):3896-3911.

［5］ BOECK R，JAEGER N A F，ROUGER N，et al.Series-coupled silicon racetrack resonators and the Vernier effect:theory and measurement［J］.Optics Express，2010，18(24):25151-25157.

［6］ JIN L，LI M Y，HE J J.Highly-sensitive silicon-on-insulator sensor based on two cascaded micro-ring resonators with vernier effect［J］.Optics Communications，2010，284(1):156-159.

［7］ WANG Sh J.Research of integrated optical ring resonator［D］.Hangzhou:Zhejiang University，2008:4-7(in Chinese).

［8］ MA H L，JIN Zh H，DING Ch，et al.Optimal design of ring resonator in silica optical waveguide［J］.Chinese Journal of Lasers，2005，32(10):1330-1332(in Chinese).

［9］ HAN X Y，PANG F F，CAI H W，et al.An integrated optical device-waveguide ring resonator［J］.Laser＆ Optoelectronics Progress，2004，41(8):26-31(in Chinese).

［10］ WU T F，LIANG Zh G，YAN J H，et al.The progress on distance measuring technique with a femtosecond optical frequency comb［J］.Metrology ＆ Measurement Technology，2011，31(5):41-44(in Chinese).

［11］ YU H.Study on measure of femtosecond laser pulse width［J］.Laser Technology，2013，37(5):679-681(in Chinese).

［12］ SUN R Y，LIU J，TAN F Zh，et al.All-fiber amplication and application of 100ps laser pulse ［J］.Laser Technology，2013，37(4):417-420(in Chinese).

［13］ YING D Q，ZHENG Y M，MA H L，et al.Splitting phenomenon of resonance dips in two-frequency serrodyne modulation r-fog［J］.Chinese Journal of Sensors and Actuators，2007，20(6):1244-1248(in Chinese).

［14］ YING D Q.Resonator fiber optic gyro based on digital triangle wave phase modulation［D］.Hangzhou:Zhejiang University，2008:13-15(in Chinese).

［15］ MA H L，JIN Zh H，DING Ch，et al.Research on signal detection method of resonator fiber optical gyro［J］.Chinese Journal of Lasers，2004，31(8):1001-1005(in Chinese).

［16］ GRIFFEL G.Vernier effect in asymmetrical ring resonator arrays［J］.IEEE Photonics Technology Letters，2000，12(12):1642-1644.