颜色编码正弦条纹实现孤立动态物体3维测量

王 慧，白乐源，麻 珂，张启灿

(四川大学电子信息学院，成都610064)

引 言

基于结构光投影的光学3维传感技术，是测量高度随着时间变化的3维动态物体最常用的方法。在最近的几年，它也是一个比较热门的研究方向，有很多方法先后被提出［1-3］，主要采用了傅里叶变换轮廓术(Fourier transformation profilometry，FTP)［4-6］、相位测量轮廓术(phase-measuring profilometry，PMP)［7］和彩色编码条纹投影技术［8-12］。其中，PMP测量精度较高，但是需要至少3幅图，适合测量静态物体;FTP测量速度快，只需要1幅图即可获取物体的3维面形。若被测物体分布具有高陡度或存在若干孤立区域时，采用上述2维空间相位展开算法很难可靠地展开相位。为此，颜色编码条纹投影技术［9-11，13］把彩色编码结构光测量原理和相位测量结合起来，编码之后的颜色信息有助于数据处理和条纹级次判别，从而用来指导相位的展开［9，11，13-14］。这种方法适合于测量空间分布不连续的孤立物体。

在同行研究提出的颜色编码条纹投影技术基础上，作者提出了一种新的颜色编码条纹方法，用于测量孤立动态物体的3维面形。该算法编码简单、解码快速可靠，给分布不连续的孤立动态物体3维面形测量带来极大的方便。模拟和实物实验均验证了本文中方法的实用性。

1 投影颜色编码条纹的3维面形方法

1.1 测量方法的原理框架

本方法以颜色编码条纹投影技术为基础，采用排列顺序固定且已知的彩色编码序列，将每一个正弦条纹周期都进行颜色编码标记。拍摄记录物体表面的彩色编码条纹图像后，对整幅图像分离提取出正弦光栅对应的强度分布，经过傅里叶条纹分析后计算得到截断相位信息;同时对图像进行分色处理获取每一根颜色条纹的颜色级次，依据编码时颜色级次和条纹级次一一对应的关系，还原每一个正弦光栅周期的对应级次，用来指导截断相位的正确展开，从而恢复物体的高度信息。该方法在解码和3维重建阶段的算法流程图如图1所示。

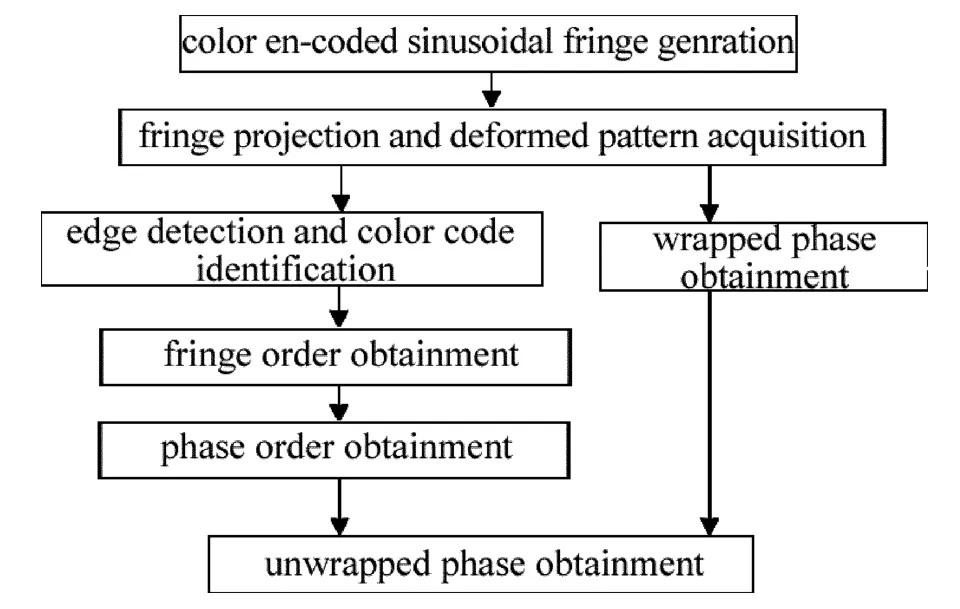
Fig.1 Algorithm flow

由于每一个正弦光栅条纹周期都有自己唯一确定的编码信息，它能确定给出对应条纹周期的相位级次，相位级次乘于2π后叠加上该周期内的截断相位，就得到了展开相位的真值。该方法使相位展开过程变成逐条纹周期的级次信息与截断相位的求和运算，而不是空间相邻两个条纹周期间的级次加减运算，避免了相位空间展开的误差累加传递，非常适用于无空间关联信息的孤立物体的3维面形测量。

1.2 编码设计

在红、绿、蓝三基色按不同的比例混合组成的RGB颜色空间里，每一个颜色都有红绿蓝3个通道，每个像素点的颜色数值定义如下:

表1中举例说明了从二进制码到颜色数值之间的对应关系。

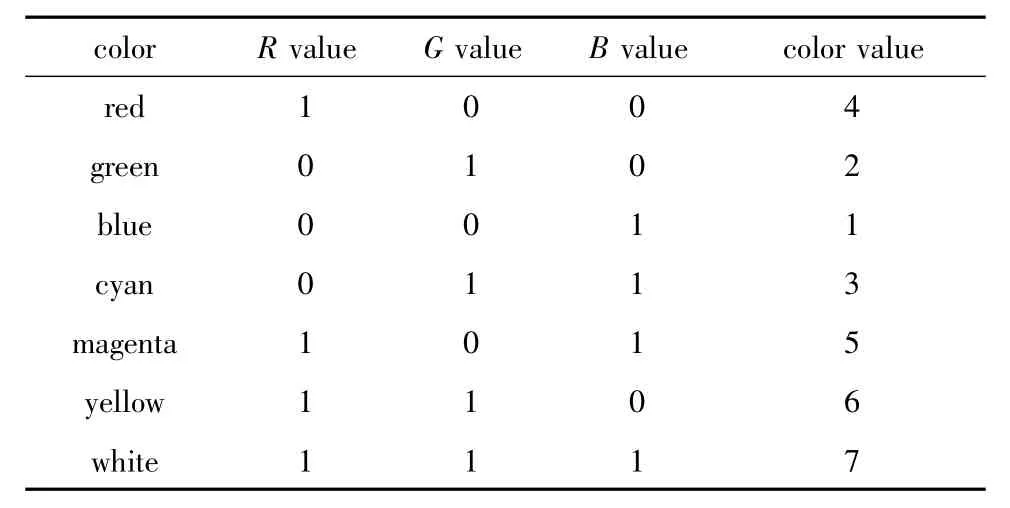
Table1 Color and color value of binary value in RGB model

由于黑色不能携带正弦条纹的强度信息，本编码方法中没有选择黑色，只使用其余7种颜色。本文中使用两级编码方式获得编码后的颜色序列，为了提高色条周期识别的精度，不希望相邻色条的颜色相同［9，13］。第1级编码由白色、基色补色和基色构成，编码长度为5。白色较容易被识别确定，被排列在中央，用于标记每个第1级编码排列，从内向外依次是为白色补色和基色，比如蓝色、黄色、白色、青色和红色，称之为内部级次。按照这样的约定生成同类型的6组排列A～F，分别如表2中所示。

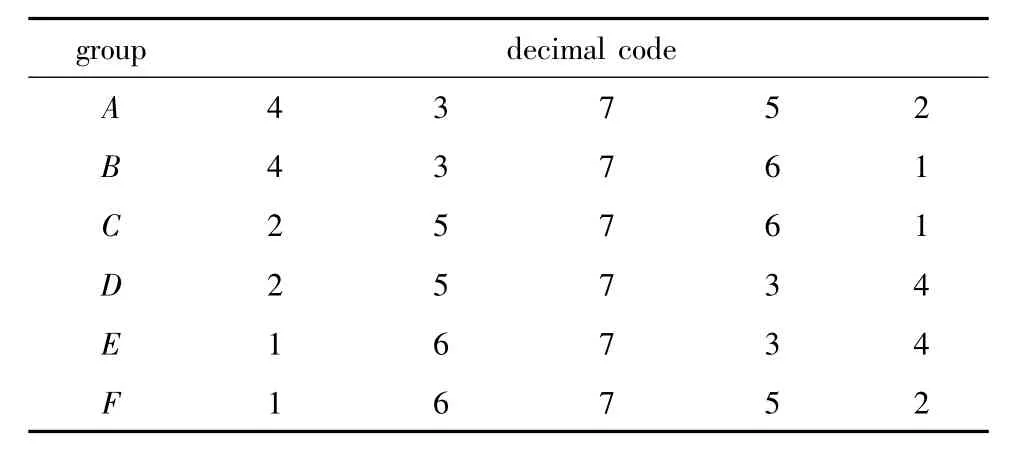
Table 2 Color group of the first level

第2级编码就是这6组第1级编码的再次排列组合的结果。同样，为了便于后期的解码，约定前后两组第1级编码的相邻色条的颜色不能相同，比如C，D不能直接排在A后面(因为同是绿色2)。经过这样的约定限制后，其中可用的一个排列组合为ABCDEFAECBDFBAFEDCA。每一个第1级编码在第2级编码中都有特定的位置，称之为外部级次。从排列中可以看出每根颜色条纹的内部级次和外部级次都是唯一确定的。内部级次和外部级次之和是颜色级次，一旦某一条纹的颜色级次被确定，那相应的条纹级次就可以被确定。

从编码方式可以看出，本文中的编码序列满足以下条件:(1)与补色相邻的颜色必定为基色或者白色，每组条纹的中心条纹颜色必是白色;(2)相邻两组编码之间相接的颜色必定是基色。编码生成的总色条数是19×5=95，也就是说，可以用来编码标记95个正弦光栅条纹周期，这已经满足大多数测量的需求了。图2a显示了第1级编码E中5种颜色的排列，图2b中给出了全部编码色条的一部分，每一种颜色用相应的英语单词的第1个大写字母作为标注。

Fig.2 a—a series color b—part of color sequence c—sinusoidal fringe d—the projected fringe pattern

从编码设计过程可以得出编码色条图的3个特性:(1)每相邻的3根色条为一组，并且在本组只出现一次;(2)每相邻的4根色条只在本组中唯一出现;(3)相邻的两组第1级编码色条组合在整个编码序列里只出现一次。合理的应用编码特性可以准确快速地进行解码，同时利用编码条件可以对恢复的颜色进行修正。

将图2b所示的颜色编码序列和图2c所示的正弦强度条纹融合在一起，得到图2d所示的颜色编码正弦条纹，编码结果图案的数学表达式为:

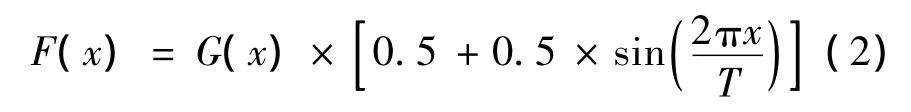
式中，G(x)表示颜色序列;T既是正弦条纹的周期，也是每个编码色条的像素宽度。正弦条纹的强度最小值点对应编码色条的变换边界，也就是说，在整个颜色编码条纹序列里中，条纹级次和颜色级次是一一对应的。

1.3 解码过程

拍摄受高度调制的彩色变形条纹图像之后，提取条纹强度信息进行傅里叶变换获取截断相位信息，同时对该图像的颜色信息进行解码获取颜色级次和相位级次，指导完成相位的正确展开，从而可以重建被测物体的3维面形分布。

(1)将所拍摄的彩色变形条纹由RGB空间转换到根据色度、饱和度和亮度的方式叠加(hue saturation value，HSV)空间里，并提取强度信息V分量，对其进行傅里叶变换得到截断相位φ(i，j)。提取截断相位的边界信息，作为对应色条区域的边缘。为了提升后期颜色还原操作的准确性、降低其难度，在实际测量前，采用参考文献［15］中所述的颜色校正模型和方法，对测量系统进行各颜色通道校准。执行颜色校准后，色条中心处的颜色还原更为可靠，提取色条中心区域的颜色来填充相应的颜色区域，得到变形条纹对应的颜色图。

(2)获取颜色级次和条纹级次:将步骤(1)中恢复的颜色图，进行三通道分离并二值化，求出每根条纹的颜色数值，并利用编码的约束条件对局部判断错误的还原颜色进行修整;判断出每根色条的内部级次和外部级次，二者相叠加，即可得到整场的条纹级次n(i，j)。

(3)把所得到的条纹级次n(i，j)和截断相位φ(i，j)进行叠加即可获得条纹的展开相位Φ(i，j)，即:

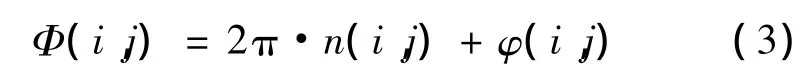
图3所示的是整个解码的过程，左侧图片是实际实验处理过程中的局部区域，右侧是相应区域中间行的数据。

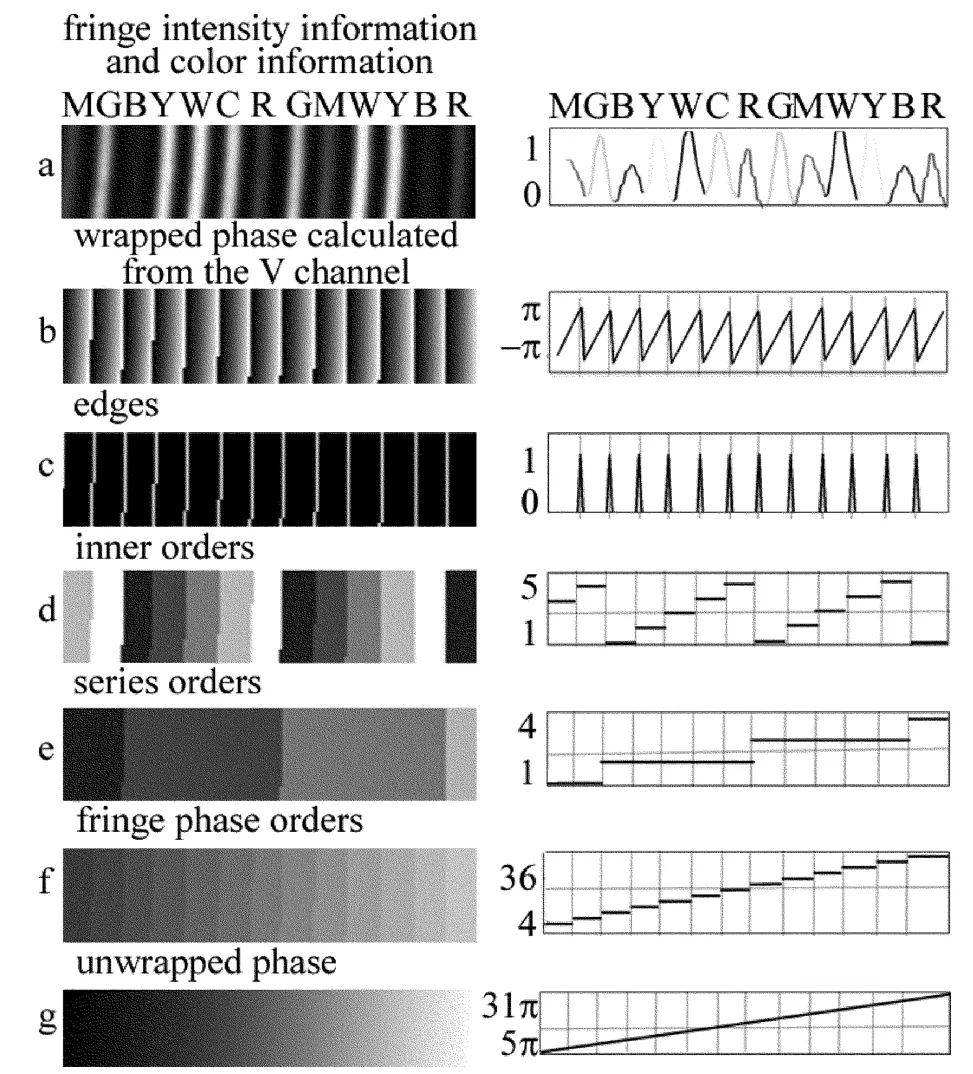
Fig.3 Image processing stages

2 实验结果和分析

Fig.4 Result of simulation experiment

为了验证本文中提出的颜色编码正弦条纹光栅投影测量方法的可行性，使用3Dmax模拟实验平台进行条纹的投影和采集。处理过程如图4所示，被测物体为两个孤立的规则球。图4a为采集的彩色变形条纹;提取其中的变形条纹强度信息如图4b所示;图4c为从图4a提取的颜色信息;图4d为采用傅里叶变换方法从图4b中获得的截断相位;图4e是根据颜色信息获取的条纹级次;图4f为最后的展开相位。模拟实验结果验证了该测量方法的可行性。

为了验证本文中编码及解码过程的实用性，对其进行了实物实验。空间彼此孤立、高度大致相当的3个模具被紧密固定在1个旋转台上，转台驱动3个模具绕1个公共转轴旋转，且相对位置保持不变。采用本文中前面方法编码、周期为8个像素的彩色编码光栅条纹经爱普生LCD投影仪(EMP-280)投影到该转动物体表面，用Basler彩色相机(pIA640-210gc)连续采集旋转过程中的彩色编码变形光栅图像。事后，处理了29幅变形条纹图，其中3幅如图5a，图5b和图5c所示，对应重建的结果依次如图5d，图5e和图5f所示。由于该测量系统未经过标定，图中3维展示的是连续相位分布，一旦测量系统标定，就能转换映射为真是高度分布。从实验结果可以看出，本文中的彩色编码光栅能正确重建动态物体孤立变化的3维面形分布。

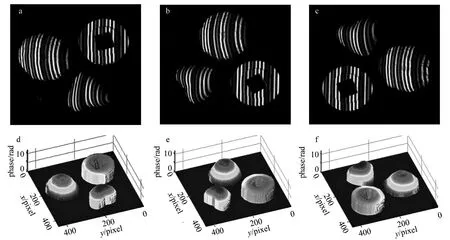
Fig.5 Experiment on dynamic and spatially isolated objects

3 小结

提出一种用于孤立动态物体3维面形测量的颜色编码正弦条纹投影方法，该方法利用2级编码的颜色信息来编码每一个正弦条纹周期，利用此带有颜色信息的条纹图案来记录测量空间孤立动态物体的3维面形数据。只利用一幅图像，快速准确地利用内部级次和外部级次叠加来获取条纹的相位级次，与傅里叶变换得到的截断相位进行叠加，能够较好地完成相位展开，从而恢复孤立动态物体的3维面形。该算法中编码简单稳定、解码方式快速可靠，模拟实验和实物实验的结果都验证了该方法的可行性。

［1］ ZHANG S，VANDERWEIDE D，OLIVER J.Superfast phaseshifting method for 3-D shape measurement［J］.Optics Express，2010，18(9):9684-9689.

［2］ ZHANG Q C，SU X Y.High-speed optical measurement for the drumhead vibration ［J］.Optics Express，2005，3(8):3110-3116.

［3］ LI Y，ZHAO C F，QIAN Y X，et al.High-speed and dense three-dimensional surface acquisition using defocused binary patterns for spatially isolated objects［J］.Optics Express，2010，18(21):21628-21635.

［4］ TAKEDA M，MUTOH K.Fourier transform profilometry for the automatic measurement of 3-D object shapes［J］.Applied Optics，1983，22(24):3977-3982.

［5］ SU X Y，CHEN W J.Fourier transform profilometry:a review［J］.Optics and Lasers in Engineering，2001，35(5):263-284.

［6］ SU X Y，ZHANG Q C.Dynamic 3-D shape measurement method:a review［J］.Optics and Lasers in Engineering，2010，48(2):191-204.

［7］ LI Y，SU X Y.A new method f or system calibration in phase measurement profilometry with large view field［J］.Acta Optica Sinica，2006，26(8):1162-1166(in Chinese).

［8］ ZHU Q Y，SU X Y，XIAO Y S.3-D shape measurement method with max-difference color-coding structured light［J］.Laser Technology，2006，30(4):340-343(in Chinese).

［9］ MA K，ZHANG Q C.A new color structured light coding method for Three-Dimensional measurement of isolated object［J］.Chinese Journal of Lasers，2010，37(11):2918-2924(in Chinese).

［10］ LIU W Y，WANG Z Q，MU G G.Three-Dimensional surface profilomentry using color-coded projection grating［J］.Acta Optical Sinica，2001，21(6):687-690(in Chinese).

［11］ WANG N，ZHANG Q C，MA K.3-D shape measurement for isolated objects based on color-encoded fringe projection［J］.Journal of Optoelectronics·Laser，2010，21(8):1227-1231(in Chinese).

［12］ YU X Y，WU H B.3-D measurement technology by structured light based on fringe edge decoding［J］.Chinese Journal of Electron Devices，2008，31(2):390-392(in Chinese).

［13］ SU W H.Color-encoded fringe projection for 3-D shape measurement［J］.Optics Express，2007，15(20):13167-13181.

［14］ SU X Y，CHEN W J.Reliability-guided phase unwrapping algorithm:a review ［J］.Optics and Lasers in Engineering，2004，42(3):245-261.

［15］ MA K，ZHANG Q C.A new method to reduce the influence of object’s color texture in three-dimensional shape measurement［J］.Journal of Optoelectronics·Laser，2011，22(4):582-587(in Chinese).