基于有限元分析方法的某惯性台体结构优化设计

陈兴好，余盛强，闫红松

（北京自动化控制设备研究所，北京100074）

基于有限元分析方法的某惯性台体结构优化设计

陈兴好，余盛强，闫红松

（北京自动化控制设备研究所，北京100074）

摘要：建立惯导系统中惯性组件结构三维模型，利用有限元分析软件对惯性组件结构进行有限元模态计算和分析。根据模态分析结果，对惯性台体结构进行拓扑优化，达到惯性台体减重的目的，优化后的惯性台体结构满足文中提出的设计要求。此结构优化设计方法简单，易于实现，对优化惯导系统结构设计，实现小型化、轻量化目标具有一定的指导意义。

关键词：惯性台体；有限元模态分析；拓扑优化；结构优化设计

0　引言

惯导系统作为惯性坐标基准和惯性测量装置，广泛应用于各种运载火箭、导弹及其它载体中，其工作精度和可靠性直接影响着载体的控制精度和可靠性。随着航天技术和国防事业的日益发展，现代军事技术对新型号惯导系统不仅要求具有更高的精度和可靠性指标，而且要求具有系统小型化、重量轻、定型快以及适应大过载、大冲击等恶劣力学环境条件的特点[1]。

惯性台体是惯导系统中的重要结构零件，是陀螺仪、加速度计等高精度惯性仪表的安装基座，因此惯性台体的刚强度非常重要。对惯性台体进行有限元模态分析，以确定其固有频率和振型，从而避免系统工作时发生共振和出现有害振型，是惯性台体结构设计中不可或缺的过程[2]。本文借助有限元分析技术，通过有限元模态计算结果，对惯性台体进行相应的结构优化设计，从而实现惯性台体小型化，轻量化的目标。

1　惯性台体组件设计及仿真分析

1.1模态分析基本理论

模态分析[3]的目的是计算结构固有频率和主振型，此类问题可归结为特征值和特征向量问题。动力学问题的有限元法基本方程：

对于无阻尼振动，式（1）中令阻尼力项和外加激励项为0，则有：

任何弹性体的自由振动都可以分解为一系列的简谐振动的叠加，设式（2）的简谐振动解为：

式中ϖ为结构振动固有频率，将式（3）代入自由振动基本方程可得：

由于自由振动时，结构中各节点的振幅δ0不全为0，故方程组系数的行列式值必为0，即：

1.2惯性台体设计

以某型惯性台体设计为例，其设计要求如表1所示。建立惯性台体组件三维模型，台体组件主要由台体、3个陀螺仪、3个加速度计等构成，其中6个惯性仪表（3个陀螺仪、3个加速度计）安装在台体上。

表1　惯性台体设计要求Tab.1 Design requirements of the inertial platform

为了提高仿真计算效率，在导入有限元分析软件分析之前，对台体组件模型进行了适当的简化处理：

1）将半径小于2mm的倒圆角删除；

2）螺钉简化为和螺纹孔中径大小一致的圆柱体；

3）陀螺仪、加速度计均简化为外形和实物一致的块体，质量和实物保持一致。

简化后的台体组件初始模型如图1所示，其中台体的质量为104.666g，大于55g，陀螺和加速度计的密度按实际情况折算。

图1　简化后惯性台体组件模型Fig.1 Simplified inertial platform component models

1.3惯性台体有限元建模

将简化后的初始模型导入有限元分析软件里进行前处理，为了提高计算精度，采用4面体10节点的高阶单元对台体组件进行网格划分，整个台体组件共划分了217977个单元，节点数为321749个，划分网格后的台体组件如图2所示。

图2　划分网格的惯性台体组件Fig.2 The meshing inertial platform component

惯性台体的材料选用硬铝合金2A12，材料参数如表2所示。边界条件是将对外连接的4个安装孔（见图1）的3个平动自由度进行约束。

表2　材料参数Tab.2 Material parameters

1.4模态计算结果与分析

通过仿真计算，台体组件的一阶频率为3431Hz，远高于弹体环境条件频率上限2000Hz，结构刚度较好。为了更好地观察惯性台体的振型，台体组件第一阶振型云图省略了6个惯性仪表，具体如图3所示。图3中颜色最深的区域1变形量最小，是重点优化减重的部位。

图3　惯性台体组件第一阶振型图Fig.3 The first mode figure of the inertial platform component

2　惯性台体结构优化设计

2.1结构拓扑优化理论基础

拓扑优化[4]是在满足结构体积缩减量的条件下使结构的柔度极小化。拓扑优化的目标是寻找承受单载荷或多载荷的物体的最佳材料分配方案，其表现为“最大刚度”设计。目标函数是在满足结构约束情况下减少结构的变形能，减小结构变形能相当于提高结构的刚度。这通过使用设计变量给每个单元赋予内部伪密度来实现。常用的连续体结构的拓扑优化方法主要有变厚度法、变密度法及均匀化方法。变密度法的实现过程相对简单，其要求材料必须为各向同性，不需引入微结构和附加的均匀化，以单元的相对密度为设计变量，用连续变量的密度函数形式来表示材料弹性模量和相对密度的对应关系，这种关系被定义后可以根据拓扑优化得到单元的密度值进行连续结构部分的取舍，对于不同的假设关系能得到不同的拓扑优化结构。

优化问题可以表述为在特定域中满足一定的约束条件下，选取适当的变量X，使得目标函数φ(X)达到最优解，数学模型表达如下：

目标函数：φ(X)=φ(x1，x2，...，xn)；

约束条件：

式中：φ(X)为目标函数，可以为最小柔度(最大刚度)，结构体积、重量；gi(X)为约束条件，可以为应力、位移等；X是设计变量构成的向量,可以是形状尺寸，拓扑变量等，、为第t个变量的最小/大值,、为第i个约束的上下限。

拓扑优化的主要流程如图4所示。

图4　拓扑优化流程图Fig.4 The topology optimization flow chart

2.2惯性台体结构拓扑优化仿真

对模型进行拓扑优化，需要首先明确设计体积与非设计体积。非设计体积指拓扑优化过程中设计者不希望发生改变的区域，优化后保持初始形状不变；设计体积是拓扑优化的优化对象，优化后设计体积各单元都有一个密度值，低密度值的单元将被删除，高密度值的单元被保留。

下面建立优化设计数学模型：

1）目标函数：目标函数是要尽量减小的数值，它必须是设计变量的函数，也就是说，改变设计变量的数值将改变目标函数的数值。本文的目标函数是使惯性台体的重量最轻，以满足表1中的设计要求。

2）设计变量：设计变量是自变量，优化结果的取得就是通过改变设计变量的数值来实现的。本文以台体的形状尺寸作为设计变量，在满足表1中设计要求的情况下，通过改变台体局部的尺寸达到减少台体重量的目的。

3）约束条件：约束条件是约束设计的数值，它们是“因变量”。约束条件可能会有上下限，也可能只有单方面的限制，即只有上限或者只有下限。本文的约束条件为惯性台体的第一阶固有频率，要求其满足表1中的设计要求。

经过优化迭代，得到的惯性台体结构的密度等值面云图如图5所示，根据拓扑优化理论，图中蓝色区域1是可进行材料删减的区域，红色区域2是材料保留区域。

图5　惯性台体结构密度等值面云图Fig.5 The density isosurface nephogram of the inertial platform structure

2.3惯性台体结构优化设计

根据拓扑优化结果，对台体进行结构优化设计，优化后的三维结构模型如图6所示。优化后惯性平台台体的质量为49.775g。

图6　优化后台体组件模型Fig.6 The optimized inertial platform component model

对优化后结构进行模态分析，台体的第一阶固有频率为3097.6Hz，台体第一阶振型图如图7所示，台体振型和优化前基本一致。

图7　优化后惯性台体第一阶振型图Fig.7 The first mode figure of the inertial platform after optimized

优化前后，台体结构的重量与频率变化如表3所示。可见，经过优化设计后，台体的质量减少了54.891g，减重率达到52.44%，台体的第一阶固有频率减小了333.4Hz，减小了9.72%，且都高于3000Hz，结构刚度能够满足设计要求。

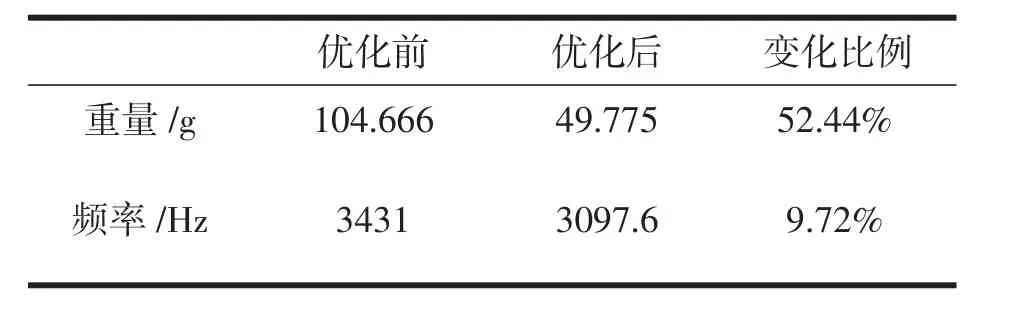
表3　优化前与优化后对比Tab.3 Comparion of results before and after optimization

3　结论

本文对惯性台体组件进行初步三维模型建模，通过有限元分析软件对惯性平台台体组件进行有限元模态分析，根据模态分析结果，在不影响惯性仪表安装精度、可靠性和不影响整个台体组件结构刚度要求的前提下，对台体结构进行拓扑优化。

借助有限元分析方法，对惯性台体进行结构优化设计，优化设计方法简单，易于实现，实现了惯性台体小型化、轻量化的目标。此方法借助大型分析软件，提高了计算效率，从而大大缩短产品的研制周期，节省研制费用，对后续惯导结构小型化、轻量化设计具有一定的指导意义。

参考文献

[1]《惯性导航系统》编著小组.惯性导航系统[M].北京:国防工业出版社，1983.

[2]钟万登，催佩勇，等.液浮惯性器件[M].北京:宇航出版社，1987:6-74，220-267.

[3]傅志方.振动模态分析理论与参数辨识[M].北京:机械工业出版社，1990.

[4]张亚欧，谷志飞，宋勇，等.ANSYS7.0有限元分析实用教程[M].北京:清华大学出版社，2004.

中图分类号：TP273

文献标志码：A

文章编号：2095-8110（2014）03-0074-05

收稿日期：2014–06–05；

修订日期：2014–06–20。

作者简介：陈兴好（1989–），男，硕士，主要从事结构设计方面的研究。E-mail:cxha103@sina.com

Structure Optimal Design of an Inertial Platform Based on the Finite ElementAnalysis Method

CHEN Xing-hao,YU Sheng-qiang,YAN Hong-song
（Beijing Institute ofAutomatic Control Equipment,Beijing 100074,China）

Abstract：The 3D model of the inertial platform component is designed by the 3D modeling software,and the finite element modal calculation and analysis of the inertial platform component are conducted with the help of the finite element software.The topology optimization of the inertial platform structure is carried out based on the modal analysis results to reduce weight of the inertial platform,and the inertial platform structure after optimized meets the need of design brought forward in the article.The method of the structure optimal design is simple and can be implemented easily, which will have certain guiding significance to the optimization of the inertial navigation system structure design and the realization of the target of miniaturization and lightweighting.

Key words:Inertial platform;The finite element modal analysis;Topology optimization;Structure optimal design